算法优化：最大子段和，最大子矩阵和，一维，二维情况分析，动态规划

最大子段和，前面b[j]理解的是：终点在j的最大连续子段和，及从k:j最大和

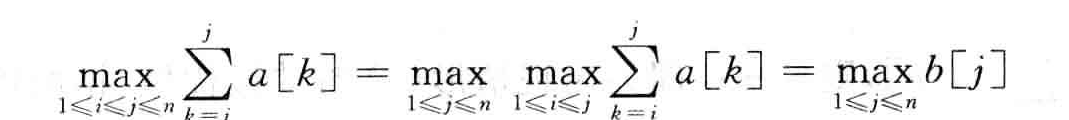
是对b[j]进行动态规划，从k:j最大和：取决于k:j-1的最大和，他大于0的话，就为k:j-1的最大和+arr[j],他小于0的话，就只是arr[j]

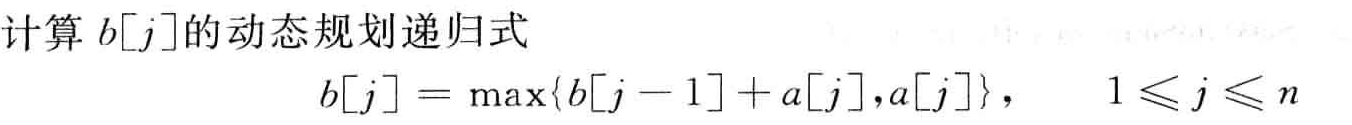
终点在j一共有n种情况，原问题只是求b[j]的最大值

从上面可以看出，终点在j的最大连续子段和这个还是很刁钻的，解决问题你不从原问题直接去分解，而去想“终点在j的最大连续子段和”，怎么会想到了？

马后炮，可能从两个方向入手，一是纯粹从解析式入手，纯推导，分解max的定义域，然后思考实际意义，或者不思考，直接按照数学公式处理：

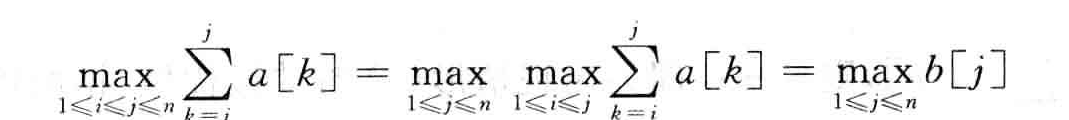
另外一种思路，从平常的算法入手思考优化，平常算法一般使用两个指针i和j,i指向子段和起始的位置，j指向子段终止的位置，然后从左往右扫描，这样原问题可以看成：起始位置为i的最大连续字段和。我们动态规划得到状态方程一般需要从n到n-1,一般情况我们需要反过来从后往前处理（参考选与不选我们都是从后往前处理的），也就是原问题可以看成：终止位置为j的最大连续字段和,这也j也可以作为状态方程的规模变量。

以上的两种思路，也可把最大子段和推广到二维上

二维的最大子段和：m*n的矩阵，求最大子矩阵和

第一种思路通过纯数学变换：

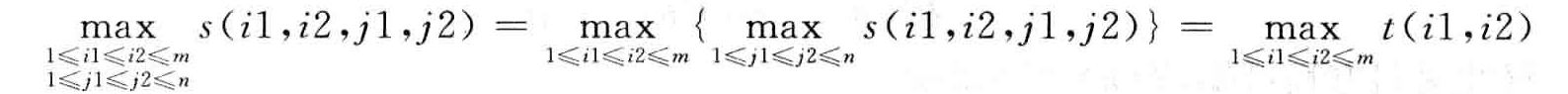
我们简化t(i1,i2)

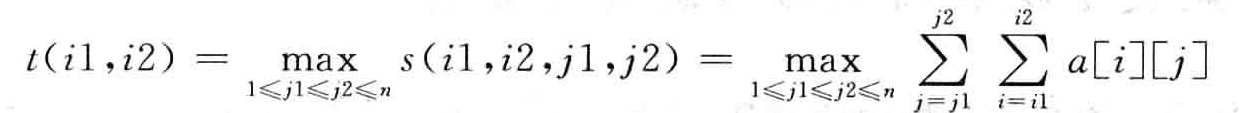
我们假设b[j],简化如下：

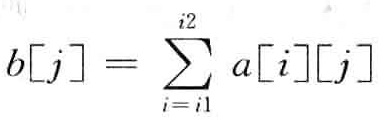
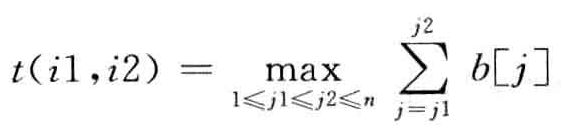
看出来了没有，t(i1,i2)是啥，他是在求数组b的最大子段和，也就是一个一维的最大字段和

回头再看原问题是啥了：max{t(i1,i2)}, 1<=i1<=i2<=m,这个只是单纯的求最大值，双针遍历n,找到最大的那个t(i1,i2)

现在对比一维和二维原问题的情况：

一维时：max{b[j]}, 1<=j<=n，b[j]可递归

二维时：max{t(i1,i2)}，1<=i1<=i2<=m，t(i1,i2)是一个一维的最大子段和，可以通过一维的方式求得。

我们再思考一下其实际的意义，得到第二种思路：一维时，b[j]可理解为终点在j的连续子段和；二维时t(i1,i2)的含义了？子矩阵行起止于(i1,i2)，把对应的每一列看成一个元素组成的数组（应该是n个）求得的最大子段和

以上二维的实现方法，也是没有直接对二维的原问题进行规约得到状态方程，而是规约为一维的问题，一维的问题也没有直接使用动态规划，只是可能解用到了动态规划

算法时间复杂度O(m^2 * n)或者O(n^2 * m), 实现的时候可以把行列长的用一维的方式解决.

代码实现如下：

#%%
# 动态规划的算法，状态方程，初始值 
# 如何划分子问题比较好了，看成选择问题，选与不选，从尾部开始，i选的话，最大值就是end_max前面
# n-1个元素的最大值+arr[i],不选的话就是前面n-1个元素求最小字段和
# 这个工作量好大，问题规模缩小了1，然后干了分治算法一层的工作量
# 所以这种规约子问题的方案不好？
# 最大字段结束在j,那么原问题的解就是j=0,1,2..len(arr)-1
# 这么多情况里面的最大值，
# 我们定义b[j]为结束在j字段和最大值，max{b[j]} 0<=j<=len(arr)-1
# 我们只要求出了每一个b[j],最大值就是可以从里面求出来了
# 那么b如何求解了,结束在j的最大字段和，假如前面j-1最大字段和小于0的话，那就是arr[j]
# 状态方程为：b[j] = max{b[j-1]+arr[j],arr[j]}
# 这里不需要考虑arr[j]是否大于0，因为我的子问题就是定义的是结束在j的最大字段和，至于
# 最终的解是结束在不同的j上的最大字段和的最大值。

# 这个方法可以知道结束位置j,没法知道起始位置i为多少啊    
def maxSumDynamicProgramming(arr):
    # 本来是需要一个数组来记录b的，然后找b[]里面的最大值
    # 但是我们得到一个b,就可以更显最优结果的，我只要记录当前最优解就行了，所以只需要当前的b
    # b的初值就是b[0-1]的值，也就是没有元素时最大字段和为多少，为0
    cur_b =0
    
    # 用于记录最优的结果
    best_result = 0
    best_j = -1
    # 根据状态方程自底向上完成
    for j in range(len(arr)):
        # b[j] = max{b[j-1]+arr[j],arr[j]}，当b[j-1]>0为左边，否则为右边，也可以直接用max
        if cur_b>0:
            cur_b += arr[j]
        else:
            cur_b = arr[j]
        
        # 每求出一个b,就更新一下当前最优解
        if cur_b >= best_result:
            best_result = cur_b
            best_j = j
    return best_result,best_j
         
#%%
import numpy as np
# 处理矩阵，把arr[i1:i2+1,:]转换成一维数组，也就是把每一列的从i1到i2相加
def matrixSumByRow(arr,i1,i2,n):
    li = [0]*n
    for j in range(n):
        for i in range(i1,i2+1):
            li[j] +=arr[i][j]
    return li

def maxSumOrder2(arr):
    # 获取矩阵的行列
    row,column = arr.shape
    # 初始化左右结果，best_j1由于一维最大子段和没有实现，这里也没有
    best_result = 0
    best_i1 = -1
    best_i2 = -1
    best_j2 = -1
    # 原问题max{t(i1,i2)}，1<=i1<=i2<=m，遍历所有的t(i1,i2)
    for i1 in range(row):
        for i2 in range(i1,row):
            # matrixSumByRow(arr,i1,i2,column)把arr[i1:i2+1,:]转换成一维数组
            # 求出这个一维数组的最大字段和，这个是原问题的一个可行解
            t_i1_i2,j2 = maxSumDynamicProgramming(matrixSumByRow(arr,i1,i2,column))
            # 如果可行解优于当前的最优解，更新为当前最优解
            if t_i1_i2 > best_result:
                best_result = t_i1_i2
                best_i1 = i1
                best_i2 = i2
                best_j2 = j2
                
    return best_result,[best_i1,best_i2,-1,best_j2]
            
        
#%%
arr = np.full((5,5),-1)
arr[1][1] = 4
arr[1][3] = 4
arr[3][1] = 4
arr[3][3] = 4
print(arr)
print(maxSumOrder2(arr))


arr = np.full((5,5),-1)
arr[1][1] = 4
arr[1][3] = 4
arr[3][1] = 4
arr[3][3] = 4
print(maxSumOrder2(arr))

[[-1 -1 -1 -1 -1]
 [-1  4 -1  4 -1]
 [-1 -1 -1 -1 -1]
 [-1  4 -1  4 -1]
 [-1 -1 -1 -1 -1]]
(11, [1, 3, -1, 3])