伯努利分布：
伯努利分布(Bernoulli distribution)又名两点分布或0-1分布，介绍伯努利分布前首先需要引入伯努利试验（Bernoulli trial）。
伯努利试验是只有两种可能结果的单次随机试验，即对于一个随机变量X而言：
伯努利试验都可以表达为“是或否”的问题。
如果试验E是一个伯努利试验，将E独立重复地进行n次，则称这一串重复的独立试验为n重伯努利试验。
进行一次伯努利试验，成功(X=1)概率为p(0<=p<=1)，失败(X=0)概率为1-p，则称随机变量X服从伯努利分布。其概率质量函数为：
伯努利分布的EX= p,DX=p(1-p)。
伯努利分布是一个离散型机率分布，是N=1时二项分布的特殊情况。
伯努利分布的典型例子：抛一次硬币是正面向上吗？刚出生的小孩是个女孩吗？
二项分布：
二项分布(Binomial distribution)是n重伯努利试验成功次数X的离散概率分布。
如果试验E是一个n重伯努利试验，每次伯努利试验的成功概率为p，X代表成功的次数，则X的概率分布是二项分布，记为X~B(n,p)。
其概率质量函数为
显然
伯努利分布是二项分布在n=1时的特例；
二项分布名称的由来，是由于其概率质量函数中使用了二项系数
，该系数是二项式定理中的系数，二项式定理由牛顿提出：
二项分布的典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率。
多项分布：
多项式分布(Multinomial Distribution)是二项式分布的推广。二项式做n次伯努利实验，规定了每次试验的结果只有两个，如果现在还是做n次试验，只不过每次试验的结果可以有多m个，且m个结果发生的概率互斥且和为1，则发生其中一个结果X次的概率就是多项式分布。
扔骰子是典型的多项式分布。扔骰子，不同于扔硬币，骰子有6个面对应6个不同的点数，这样单次每个点数朝上的概率都是1/6（对应p1~p6，它们的值不一定都是1/6，只要和为1且互斥即可，比如一个形状不规则的骰子）,重复扔n次，如果问有k次都是点数6朝上的概率就是：
多项式分布一般的概率质量函数为：
如：
假设萤火虫对食物的喜欢次序为：花粉，蚜虫，面团。假设20%的萤火虫喜欢花粉，35%的萤火虫喜欢蚜虫，45%的萤火虫喜欢面团。我们对30只萤火虫做实验，发现8只喜欢花粉，10只喜欢蚜虫，12只喜欢面团，则这件事的概率为
贝塔分布：
介绍贝塔分布(Beta distribution)之前，需要先明确一下先验概率、后验概率、共轭分布的概念。
具体可以看这篇文章：https://blog.csdn.net/zgcr654321/article/details/83478212
先验概率：
就是事情尚未发生前，我们对该事发生概率的估计。利用过去历史资料计算得到的先验概率，称为客观先验概率； 当历史资料无从取得或资料不完全时，凭人们的主观经验来判断而得到的先验概率，称为主观先验概率。例如抛一枚硬币头向上的概率为0.5，这就是主观先验概率。
后验概率：
指通过调查或其它方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正，而后得到的概率。
先验概率和后验概率的区别：
先验概率不是根据有关自然状态的全部资料测定的，而只是利用现有的材料(主要是历史资料)计算的；后验概率使用了有关自然状态更加全面的资料，既有先验概率资料，也有补充资料。
先验概率和后验概率的关系：
共轭分布(conjugacy)：
后验概率分布函数与先验概率分布函数具有相同形式。
在试验数据比较少的情况下，如果我们直接用最大似然法估计二项分布的参数可能会出现过拟合的现象（比如，扔硬币三次都是正面，那么最大似然法预测以后的所有抛硬币结果都是正面）。
为了避免这种情况的发生，可以考虑引入先验概率分布
来控制参数
，以防止出现过拟合现象。
如何选择呢？
二项分布的似然函数为：
如果选择的先验概率也与和
有次方的乘积的关系，那么后验概率分布的函数形式就会跟它的先验函数形式一样了。具体来说，选择先验概率(prior)的形式是
，那么后验概率(posterior)就会变成
。此时后验概率(posterior)和先验概率(prior)具有相同的函数形式(都是也与和次方的乘积)，这样先验概率与后验概率就是共轭分布了。
因此，我们选择贝塔分布作为先验概率，其概率分布函数为：
其中
通过分部积分法，可推导出这个函数有如下递归性质
Γ(x)函数可以看作是阶乘在实数集上的延拓，具有如下性质
狄利克雷分布：
Dirichlet分布可以看做是分布之上的分布。
在伯努利分布里，参数μ就是抛硬币取某一面的概率，因为伯努利分布的状态空间只有{0,1}。但是在多项分布里，因为状态空间有K个取值，因此μ变成了向量
。多项分布的likelihood函数形式是
，因此就像选择伯努利分布的共轭先验贝塔函数时那样，狄利克雷分布的函数形式应该如下：
上式中，
是迪利特雷参数，把上式归一化为真正的迪利特雷分布为：
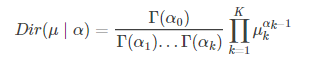
其中
。这个函数和贝塔分布有点像，跟多项式分布也有点像。就像β分布那样，狄利克雷分布就是它所对应的后验多项分布的参数μ的分布，只不过μ是一个向量。
举例：
假设我们有一个骰子，其有六面，分别为{1,2,3,4,5,6}。现在我们做了10000次投掷的实验，得到的实验结果是六面分别出现了{2000,2000,2000,2000,1000,1000}次，如果用每一面出现的次数与试验总数的比值估计这个面出现的概率，则我们得到六面出现的概率，分别为{0.2,0.2,0.2,0.2,0.1,0.1}。现在，我们还不满足，我们想要做10000次试验，每次试验中我们都投掷骰子10000次。我们想知道，骰子六面出现概率为{0.2,0.2,0.2,0.2,0.1,0.1}的概率是多少（说不定下次试验统计得到的概率为{0.1, 0.1, 0.2, 0.2, 0.2, 0.2}这样了）。这样我们就在思考骰子六面出现概率分布这样的分布之上的分布。而这样一个分布就是Dirichlet分布。
高斯分布：
其实就是正态分布（Normal distribution），又叫高斯分布。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为：
正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。下图中绿色曲线就是标准正态分布。
