转自:《编码的奥秘》 第十二章
加法是最基本的算术运算。所以,如果想要建造一台计算机(这是本书隐含讨论的问题),必须首先知道如何构造一种机器,它可以把两个数加起来。当你解决了这个问题,你会发现加法正是计算机唯一所做的事情,因为通过使用用于加法的机器,我们还可以构造用加法来实现减法、乘法、除法以及计算房产抵押款、引导向火星发射卫星、下棋和电话计费等等功能的机器。
同现代的计算器和计算机比起来,本章构造的加法机庞大、笨重、速度慢且噪声大。但有意思的是构成它的部件完全是前几章学过的电子设备,如开关、灯泡、电线、电池以及可构成几种逻辑门的继电器。这个加法机包含的所有部件都于 1 2 0年以前就已发明,而且,我们并不用真正地在屋子里建造它,只需在纸上和脑子里构造这台机器就行了。
这个加法机只能工作于二进制数,而且它缺少很多现代计算机(器)的辅助设备。它不能用键盘来敲入你想加的数,代之的你只能用一系列开关表示待加的数。它也不能用显示器显示结果,你所看到的只是一排灯泡。
但这台加法机确实实现了两数相加的功能,而且其工作方式和计算机做加法十分相似。
二进制加法与十进制加法很像。当你相加十进制数如 2 4 5 和6 7 3 时,你把问题分解成简单的步骤,每一步只对一对十进制数字相加。本例中,第 1 步是把 5和3加起来。生活中,你若能记住加法表,问题的解决就快多了。
十进制加法和二进制加法的一大区别是二进制数字的加法表要比十进制数字的加法表简单得多:

你可能在学校里记过上面这张表,并背诵过如下口诀:
把相加结果的数前加上零,可以把加法表改写成如下形式:

这样一来,二进制数字相加的结果是两位数,分别称为“和”和“进位”(比如“ 1 加1 等于0,进位是 1 ”)。现在,可以把这张二进制加法表分成两张表,第 1 张是表示“和”的表:
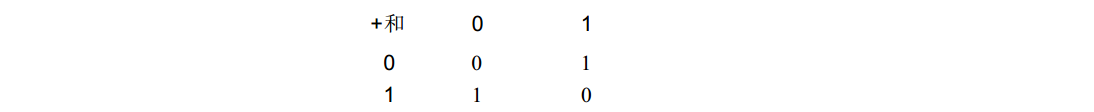
第2张是表示“进位”的表:
以这种方式来看待二进制加法就很方便了,因为加法机会分开求和与进位。构造二进制加法机需要设计一个能执行表中所描述操作的电路。因为电路的所有部件,如开关、灯泡、电线都是可以表示成二进制数的,因而该电路由于仅工作于二进制数从而大大降低了电路的复杂性。
与十进制加法一样,二进制加法也从最右边的一列开始,逐列相加两个数: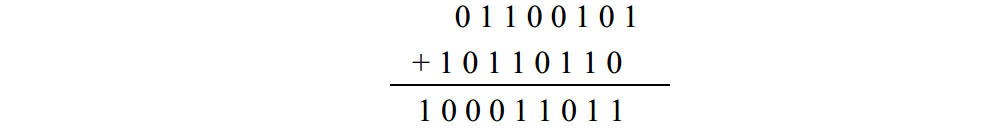
注意,当从右边加到第 3列的时候,产生了一个进位。同样的情况也发生在第 6、 7、 8列。
我们要加多大的数呢?由于这个加法机只是在脑子里构造,因而可以加很长的数字。为更合理一些,选择不超过 8位的二进制数。也就是说,操作数的范围是从 0 0 0 0 - 0 0 0 0~ 111 1 -1111,即十进制的 0~2 5 5。两个8位二进制数的和最大可以是 1 - 1111 - 111 0,即 5 1 0。
此二进制加法机的控制面板如下图所示:
板上有两行开关,每行 8个。这些开关集是输入设备,我们将用它输入两个 8位数。开关往下表示 0,往上表示 1 ,正如家里墙上的开关。输出设备在板的底部,是一行灯泡,共 9个。这些灯泡用来表示加法的结果,不亮的灯泡表示 0,亮的表示 1 。我们用了 9个灯泡是因为两个8位数相加的结果可能是 9位数。
加法机的余下部分包含了以不同方式连接而成的逻辑门。开关触发逻辑门中的继电器,继电器接着点亮相应的灯泡。例如,如果我们想把 0 11 0 - 0 1 0 1 和 1 0 11 - 0 11 0加起来(即前例中显示的两个数字),需把相应的开关设置成下面的样子:

灯泡的亮暗表明答案是 1 - 0 0 0 1 - 1 0 11 。 (当然,这只是希望的情况。毕竟,我们还没有把这个加法机构造出来!)
上一章提到过本书将会用到很多继电器,本章中的 8位加法机就至少需要 1 4 4个继电器,其中每一对数进行加法操作需要 1 8个继电器( 8 × 1 8 = 1 4 4)。如果画出完整的电路图,你一定会大惊失色,任何人都无法将连成一堆的 1 4 4个继电器看得明明白白,所以我们将用逻辑门分步解决这个问题。
当你看到下面两个 1 位二进制数相加的进位表时,你可能立刻会想到逻辑门和二进制加法之间有某种联系:

你也许已意识到这和上章所述的与门的输出是一样的:

所以,与门可以用来计算两个 1 位进制数位相加得到的进位。
看来我们已取得一点儿进展了,下一步就要看看有没有继电器能完成下面的工作:
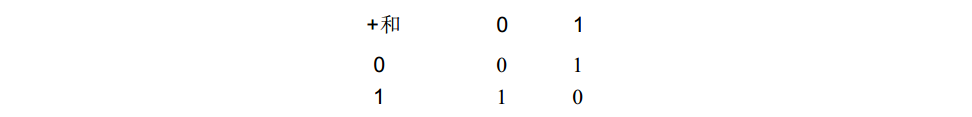
这是二进制加法运算中的另一半问题,虽说表示和的这一位不如进位那么容易实现,但我们会有办法
首先应意识到或门的输出和我们所期望的很近似,只是右下角的结果不同: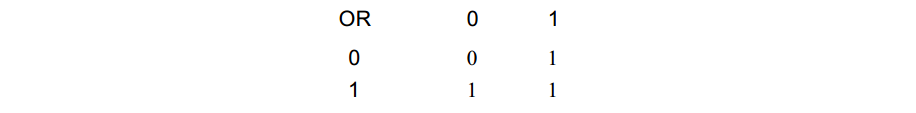
而对于与非门而言,除了左上角的输出不同以外,其他结果也与期望的一样:

所以,使用相同的输入,让我们把与非门和或门连接起来:

下表总结了或门和与非门的输出,并将其结果和加法机所要求的结果进行比较:

注意,当或门和与非门的输出都为 1 时,就可以得到期望的结果 1 ,这暗示着把两个输出作为与门的输入:
好,这样就能满足要求了。
整个电路仍然只有两个输入,一个输出。两个输入既连到了或门,也连到了与非门。或门和与非门的输出作为与门的输入,从而得到预期的结果:

这个电路有它自己的名字,称为“异或门( Exclusive OR gate 或 X O R)”。异或门输出为1 时, A输入为 1 或B输入为 1 ,但不能同时为 1 。不用再去画一个或门、一个与非门和一个与门,可以用电气工程师规定的符号来表示它:

它看上去和或门很像,只是在输入端还有一条曲线。异或门的行为表示如下:
异或门是本书需要详细描述的最后一个逻辑门(在电气工程中有时还会遇到第六个门,称为“同或门”,同或门只有两个输入相等时输出才为 1 。同或门描述的输出情况正好和异或门相反,所以这个门的符号和异或门相同,同时在输出端有一个小圆圈)。
让我们来总结一下。两个二进制数相加产生两个表,一个是表示“和”的表,另一个是表示“进位”的表:
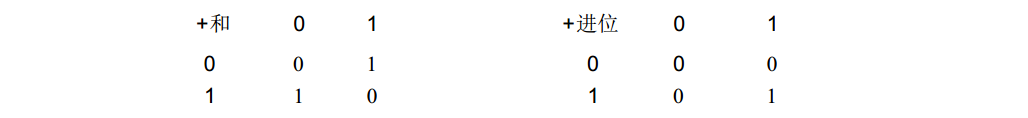
用下面两个逻辑门可以得到同样的结果:

二进制数的“和”可以由异或门得到,而“进位”可以由与门得到,所以可以把异或门和与门结合起来来完成两个二进制数 A和B的加法:

不用画与门和异或门,可以把上图简单地表示成如下的样子:
其中的方块称为“ 半加器( Half Adder)”,它可以把两个二进制位 A 和 B相加,从而得到一个和输出 (简称S) 和一个进位输出 (简称C O )。但大部分二进制数是多于 1 位的,半加器不能够把前一步的进位加到本次运算中。例如做如下加法:

只能用半加器来计算最右边一列数:即 1 加1 等于 0,进位为 1 。对于右边第 2列数,由于进位的存在,需要加 3 个数。接下来的几列都有这个问题,每一列二进制位的加法都包括了来自前一列的进位。
要把3个二进制数相加,需要按如下方式把两个半加器和一个或门连接起来:

要理解它的工作原理,先从最左边第一个半加器的 A 输入和 B 输入开始,其输出是一个和及相应的进位。这个和必须和前一列的进位输入 (简称CI) 加起来,然后把它们输入到第二个半加器。第二个半加器的和输出是最后的和。两个半加器的进位输出又输入到一个或门,或门产生了本次加法的进位输出。你可能会想这里还需要一个半加器,这当然是可行的。但当你把所有的可能情况考虑完,你会发现两个进位不可能同时为 1 。当两个输入不能同时为 1时,或门已足够用于表示两个进位的加法,此时或门和异或门的功能是相同的。
上图可简化表示为下面的方块图,称其为“ 全加器( Full Adder)”:
下面的表是对全加器所有可能的输入及其相应输出的小结:
前面说过加法机需要 1 4 4个继电器,这个数目是如何得到的呢?每个与门、或门、与非门都需要 2个继电器,所以,一个异或门需 6个继电器。一个半加器由一个异或门和一个与门构成,所以它要 8个继电器。 1 个全加器需要两个半加器和一个或门,所以它要 1 8个继电器。对于8位二进制加法机而言,共需 8个全加器,因而总共是 1 4 4个继电器。
回想一下本章最开始那个带开关和灯泡的控制面板:
现在可以把这些开关和灯泡连接成全加器了。
首先把最右边的两个开关和一个灯泡连到一个全加器上,如下图所示:
当把两个二进制数相加时,第 1 列的处理有所不同。因为接下去的几列可能包括来自前面加法的进位,而第 1 列不会有进位,所以全加器的进位输入端是接地的,这表示输入为“ 0”。第1 列相加后很可能会产生一个进位输出,这个进位输出是下一列加法的输入。
对于接下去的两个二进制位和灯泡,可以按如下办法连接全加器:

第一个全加器的进位输出是第二个全加器的进位输入。接下去的每一列数都以这种方式连接,每一列的进位输出都是下一列的进位输入。
第八个灯泡和最后一对开关连到最后一个全加器上,连接方式如下图所示:

这里最后的进位输出连到第九个灯泡上。
这样, 8个全加器就构造成功了。
还可以用另一种方式来看 8个全加器的集成,每个全加器的进位输出都是下一个全加器的进位输入:

下面是一个完整的屏蔽在一个盒子里的 8位加法器。输入是 A和B标识为从A0~A7及B0~B 7。输出为和输出,标识为从 S0~S 7:
这是标识多位数字的常用方法。下标为 0的位 A0、 B0和 S0表示最右边的、最不起眼的位。而位A7、 B7和S7是最左边的、最引人注目的位。例如,下面展示的是这些字母是如何用来表示二进制数 0 11 0 - 1 0 0 1 的:

下标始于 0,且向高位递增的原因是它们和 2的乘方数(幂)是对应的:

如果把每个二进制位和对应的 2的幂次方相乘再依次相加,你就会得到 0 11 0 - 1 0 0 1 的十进制数表示,即 6 4 + 3 2 + 8 + 1 = 1 0 5。
8位加法器的另一种画法是:
双线箭头包含了 8个输入端,代表一组 8个分开的信号。它们标识为 A7… A0、 B7…B 0、 S7… S0也用来表示一个 8位二进制数。
一旦构造了一个 8位加法器,就可以构造另一个加法器。把它们级联起来可以很容易地构成1 6位加法器:
右边加法器的进位输出连到左边加法器的进位输入端。左边加法器的输入包含了两个加数的高8位,同时产生了结果的高 8位。
现在,你可能会问: “计算机真的是以这种方式把数字加起来的吗?”
基本上是这样的,但不完全是。
首先,加法器应该做得更快。如果你明白这个电路是如何工作的,你会看到最低位相加产生的进位作为下一列数相加的一个输入,而第 3 列的加法又等着第 2列加法的进位,依此类推。加法器总体的速度等于加数的位数乘以单个全加器的速度。这种进位方式称为行波进位 。更快的加法器使用称为先行进位 的加法电路,从而加快了加法进程。
第二(但是十分重要),计算机再也不用继电器了!尽管它们曾经用过。建于 2 0世纪 3 0年代初的第一批数字计算机使用继电器,后来又用了真空管。现代计算机用晶体管。当用在计算机中时,晶体管和继电器的功能差不多,但是晶体管速度更快,体积更小,更安静,更省电,而且还便宜不少。构造一个 8位加法器仍然需要 1 4 4个晶体管(如果采用先行进位,则需要更多) ,但整体电路的体积却小多了。