圆周运算

  正如卷积是由反褶，时移，调制，相加等基本运算组成的，在后面学习到的圆周卷积中，也是由基本运算组成的，不过这些基本运算不是简单的反褶、时移，而是圆周反褶和圆周时移，那么到底与一般的反褶和时移有什么不同呢？

  其实圆周运算是针对周期序列而言的，由于周期序列在每一个周期内的取值都相同，所以我们只关注它的主值区间，比如，如果一个序列的长度为 $N$的话，那么它的主值区间就是 $0\leq n\leq N-1$。

  虽然圆周运算是源自于对周期信号的处理，但是经过一般化的扩展之后，对有限长序列也可以进行圆周运算。具体就是，你可以把有限长序列以它的长度为周期，进行周期延拓成一个周期序列，然后进行运算，然后取其主值区间进行观察得到的结果。

圆周反褶

  圆周反褶就是一个周期序列进行反褶之后，取其主值区间序列。因为一个周期序列反褶之后还是周期序列，所以这么做是合理的。

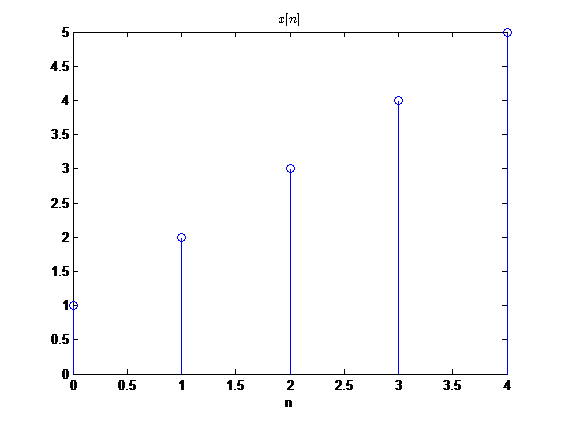
  假设一周期信号在其主值区间的取值为 $x[n]=\{x[0],x[1],x[2],x[3],x[4]\}$即该序列的周期为 $5$，那么反褶后的信号为(只关注主值区间)
$\begin{aligned} y[0]&=x[0]=x[0] \\ y[1]&=x[-1]=x[5-1]=x[4] \\ y[2]&=x[-2]=x[5-2]=x[3] \\ y[3]&=x[-3]=x[5-3]=x[2] \\ y[4]&=x[-4]=x[5-4]=x[1] \end{aligned}$
  为了方便用数学的语言描述这种运算，首先看一种数学上的模运算运算，首先看几个模运算的例子：
$\begin{aligned} 2 \,mod \, 5 =2 \\ 6 \, mod \, 5 = 1 \\ -3 \, mod \, 5 = 2 \end{aligned}$

  不知道大家看出来没有，模运算其实就是求余， $2$对 $5$的余数就是 $2$， $6$对于 $5$的余数是 $1$，而 $-3$对 $5$的余数应该为 $(-3+5)\, mod\, 5=2$(加上 $5$之后不影响余数的大小，因为 $5$一直能整除 $5$， $5$对 $5$的余数一直是 $0$)

  我们把 $2 \, mod\, 5$记作 $<2>_5$，所以我们定义圆周反褶为
$y[n]=x[<-n>_N]$
其中 $N$为序列 $x[n]$的长度。

  由上面的公式可以看出，与一般的反褶不同的是，序列下标经过了一次模运算。并且经过上面的数学化的定以后，圆周运算就不仅仅只对周期信号有效了，对一般的有限长信号都是有效的。

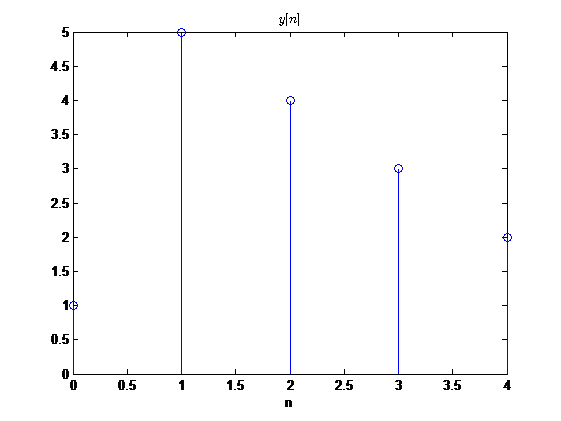
  用计算画图看一下进行圆周反褶后的效果：

扫描二维码关注公众号，回复： 4314151 查看本文章

  而一般的反褶又是什么样子的呢？还是通过计算机画图观察：

  看到这里二者发现不仅波形不一样，并且有值区间也不一样，一般反褶的有值区间变为了 $-4 \leq n \leq 0$，而圆周反褶的有值区间是 $0 \leq n \leq 4$。

  这个例子给出的就是有限长序列的圆周反褶运算，圆周运算是从周期序列扩展而来的，但不仅仅只针对于周期序列。事实上，后面的处理的圆周运算大部分都是有限长的序列。

圆周时移

  由圆周反褶的概念，不难定义出圆周时移，即：
$y[n]=x[<n-n_0>_N]$
与圆周反褶类似， $y[n]$的有值区间还是与 $x[n]$相同。

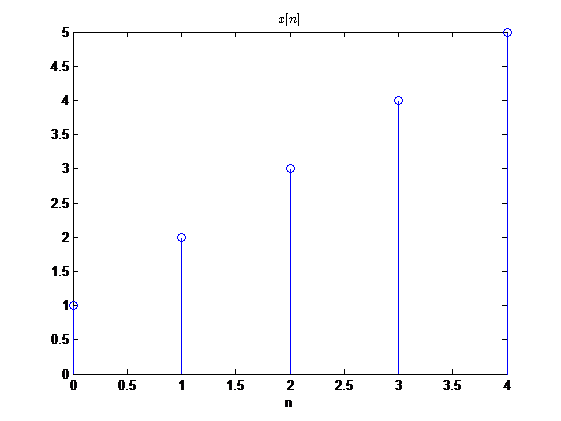
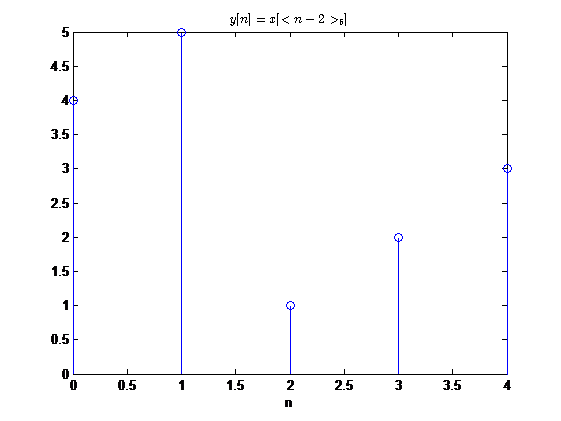
  我们来直观的感受一下，圆周时移到底是怎么一个效果：

  这完全可以看做是将序列进行周期延拓之后，然后进行时移，取其主值区间进行观察得到的结果。