

【题意】
1、第i个同学在第t[i]分钟到达车站
2、摆渡车一次可以装下无数人
3、两次发车的间隔时间m分钟
求所有等车时间和的最小值
【解题】
我们不妨认为时间是一条数轴,每名同学按照到达时刻分别对应数轴上可能重合的点。
安排车辆的工作,等同于将数轴分成若干个左开右闭段,每段的长度⩾m。原本的等车时间之和,自然就转换成所有点到各自所属段右边界的距离之和。
 .
.
令f(i)表示在第i分钟发出一班车时,所需要等待的最小时间。最后一个人到车站的时间为t
则有: f(i)=min{f(k)+∑(i-a[j],k<a[j]<=i)} 其中 0<=k<=i-m
其最终答案:ans=min{f(i)} 其中t<=i<t+m
这个DP方程的复杂度为O(t2n)
1、前缀和优化
对于∑(i-a[j],k<a[j]<=i)
令cnt[i]表示从0到i时间为止到达车站的人数和
令sum[i]表示从0到i时间为止到达车站的人的时间总和
则有∑(i-a[j],k<a[j]<=i) =i*(cnt[i]-cnt[k])-(sum[i]-sum[k])
即DP方程为 f(i)=min{f(k)+i*(cnt[i]-cnt[k]) -(sum[i]-sum[k])} 其中k<=i-m
此时,时间复杂度降为O(t2)
2、转移优化
试想一下,没有一个同学会等待超过2m分钟。
因为最坏情况下,在k时刻发出了一辆车,有位同学在k+1时刻到达了车站,摆渡车将会在k+m时刻返回,考虑到等待其他学生的情况,摆渡车最晚会在k+2m-1时刻发出(不然还不如在k+m时刻和k+2m时刻各发出一辆)
此时,DP方程为: f(i)=min{f(k)+i*(cnt[i]-cnt[k]) -(sum[i]-sum[k])} 其中i-2m<k<=i-m
此时,时间复杂度为O(tm)
3、状态压缩
很显然,根据上一条优化的结论,当顺序相邻的两位同学的时间间隔超过2m的时候,其中的状态都是无用的,可以直接压缩至2m
即对a排序后,若a[i+1]-a[i]>2m, 则对后续所有的a[k,k>i]-=a[i+1]-a[i]-2m
另外,可以将DP的起点定为第一个同学到达的时间 则最后到车站的时间t最大为2m*n
此时,时间复杂度为O(tm)=O(m2n) 解决
【代码】

1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 500 +5; 4 const int M = 100 +5; 5 const int T = 4000000 +5; 6 typedef long long ll; 7 ll n,m,t; 8 ll a[N]; 9 ll cnt[T],sum[T],f[T]={0}; 10 int main() 11 { 12 scanf("%lld%lld",&n,&m); 13 for (int i=1;i<=n;i++) 14 scanf("%lld",&a[i]); 15 sort(a+1,a+n+1); 16 // 状态压缩 17 ll dd=a[1]; 18 for (int i=1;i<=n;i++) 19 { 20 a[i]-=dd; 21 if (a[i]-a[i-1]>2*m) 22 { 23 dd+=a[i]-a[i-1]-2*m; 24 a[i]=a[i-1]+2*m; 25 } 26 cnt[a[i]]++; 27 sum[a[i]]+=a[i]; 28 } 29 t=a[n]; 30 // 求前缀和 31 for (int i=1;i<=t+m;i++) 32 cnt[i]+=cnt[i-1],sum[i]+=sum[i-1]; 33 // 边界条件 34 for (int i=0;i<m;i++) 35 f[i]=i*cnt[i]-sum[i]; 36 // DP 37 for (int i=m;i<=t+m;i++) 38 { 39 f[i]=1ll<<60; 40 for (int k=max(0ll,i-2*m);k<=i-m;k++) 41 f[i]=min(f[i],f[k]+i*(cnt[i]-cnt[k])-(sum[i]-sum[k])); 42 } 43 // 求ans 44 ll ans=1ll<<62; 45 for (int i=t;i<=t+m;i++) 46 ans=min(ans,f[i]); 47 printf("%lld",ans); 48 }
【进一步优化】
4*、斜率优化
对于:决策 f(i)=f(k)+i*(cnt[i]-cnt[k])-(sum[i]-sum[k])其中k<=i-m
和:决策 f(i)=f(j)+i*(cnt[i]-cnt[j])-(sum[i]-sum[j]) 其中k<j<=i-m
如果决策j优于决策k
即f(k)+i*(cnt[i]-cnt[k])-(sum[i]-sum[k]) > f(j)+i*(cnt[i]-cnt[j])-(sum[i]-sum[j])
化简得到:
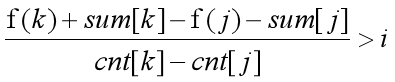
令 yk=f(k)+sum[k] xk=cnt[k]
yj=f(j)+sum[j] xj=cnt[j]
则

说明决策j优于决策k
当 k<j<i 时,若g(k,j)>g(j,i),则决策j永远不可能为最优解
所以有效点集应该呈现下凸性质 从左往右,有效点集的斜率是单调递增的 可以用单调队列来维护
此时,时间复杂度为O(nm)
【代码】
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 500 +5; 4 const int M = 100 +5; 5 const int T = 4000000 +5; 6 typedef long long ll; 7 ll n,m,t; 8 ll a[N]; 9 ll cnt[T],sum[T],f[T]={0}; 10 ll l=1,r,q[T]; 11 inline double getSlope(int u, int v) { return (double) (f[v] + sum[v] - f[u] - sum[u]) / (cnt[u] == cnt[v] ? 1e-9 : cnt[v] - cnt[u]); } 12 int main() 13 { 14 scanf("%lld%lld",&n,&m); 15 for (int i=1;i<=n;i++) 16 scanf("%lld",&a[i]); 17 sort(a+1,a+n+1); 18 // 状态压缩 19 ll dd=a[1]; 20 for (int i=1;i<=n;i++) 21 { 22 a[i]-=dd; 23 if (a[i]-a[i-1]>2*m) 24 { 25 dd+=a[i]-a[i-1]-2*m; 26 a[i]=a[i-1]+2*m; 27 } 28 cnt[a[i]]++; 29 sum[a[i]]+=a[i]; 30 } 31 t=a[n]; 32 // 求前缀和 33 for (int i=1;i<=t+m;i++) 34 cnt[i]+=cnt[i-1],sum[i]+=sum[i-1]; 35 // DP 36 l=1;r=0; 37 for (int i=0;i<=t+m;i++) 38 { 39 if (i-m>=0) 40 { 41 while (l<r&&getSlope(q[r-1],q[r])>=getSlope(q[r],i-m)) r--; 42 q[++r]=i-m; 43 } 44 while (l<r&&getSlope(q[l],q[l+1])<=i) l++; 45 f[i]=cnt[i]*i-sum[i]; // 边界情况 46 if (l<=r) f[i]=min(f[i],f[q[l]]+(cnt[i]-cnt[q[l]])*i-(sum[i]-sum[q[l]])); 47 } 48 // 求ans 49 ll ans=1ll<<62; 50 for (int i=t;i<=t+m;i++) 51 ans=min(ans,f[i]); 52 printf("%lld",ans); 53 }
