1 范数
向量的范数可以简单形象的理解为向量的长度,或者向量到零点的距离,或者相应的两个点之间的距离。
向量的范数定义:向量的范数是一个函数||x||,满足非负性||x|| >= 0,齐次性||cx|| = |c| ||x|| ,三角不等式||x+y|| <= ||x|| + ||y||。
常用的向量的范数:
L1范数: ||x|| 为x向量各个元素绝对值之和。
L2范数: ||x||为x向量各个元素平方和的1/2次方,L2范数又称Euclidean范数或者Frobenius范数
Lp范数: ||x||为x向量各个元素绝对值p次方和的1/p次方
L∞范数: ||x||为x向量各个元素绝对值最大那个元素的绝对值,如下:

椭球向量范数: ||x||A = sqrt[T(x)Ax], T(x)代表x的转置。定义矩阵C 为M个模式向量的协方差矩阵, 设C’是其逆矩阵,则Mahalanobis距离定义为||x||C’ = sqrt[T(x)C’x], 这是一个关于C’的椭球向量范数。
2 距离
欧式距离(对应L2范数):最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中。n维空间中两个点x1(x11,x12,…,x1n)与 x2(x21,x22,…,x2n)间的欧氏距离:

也可以用表示成向量运算的形式:

曼哈顿距离:曼哈顿距离对应L1-范数,也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上,坐标(x1, y1)的点P1与坐标(x2, y2)的点P2的曼哈顿距离为: ,要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。
,要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。
切比雪夫距离,若二个向量或二个点x1和x2,其坐标分别为(x11, x12, x13, ... , x1n)和(x21, x22, x23, ... , x2n),则二者的切比雪夫距离为:d = max(|x1i - x2i|),i从1到n。对应L∞范数。
闵可夫斯基距离(Minkowski Distance),闵氏距离不是一种距离,而是一组距离的定义。对应Lp范数,p为参数。
闵氏距离的定义:两个n维变量(或者两个n维空间点)x1(x11,x12,…,x1n)与 x2(x21,x22,…,x2n)间的闵可夫斯基距离定义为:

其中p是一个变参数。
当p=1时,就是曼哈顿距离,
当p=2时,就是欧氏距离,
当p→∞时,就是切比雪夫距离,
根据变参数的不同,闵氏距离可以表示一类的距离。
Mahalanobis距离:也称作马氏距离。在近邻分类法中,常采用欧式距离和马氏距离。
3 在机器学习中的应用
L1范数和L2范数,用于机器学习的L1正则化、L2正则化。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
其作用是:
L1正则化是指权值向量w中各个元素的绝对值之和,可以产生稀疏权值矩阵(稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. ),即产生一个稀疏模型,可以用于特征选择;
L2正则化是指权值向量w中各个元素的平方和然后再求平方根,可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合。
至于为什么L1正则化能增加稀疏性,L2正则化能防止过拟合,原理可查看参考资料。
参考资料:
http://blog.csdn.net/v_july_v/article/details/8203674
http://blog.csdn.net/jinping_shi/article/details/52433975
什么是范数?
我们知道距离的定义是一个宽泛的概念,只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念,它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解,我们可以把范数当作距离来理解。
在数学上,范数包括向量范数和矩阵范数,向量范数表征向量空间中向量的大小,矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是,对应向量范数,向量空间中的向量都是有大小的,这个大小如何度量,就是用范数来度量的,不同的范数都可以来度量这个大小,就好比米和尺都可以来度量远近一样;对于矩阵范数,学过线性代数,我们知道,通过运算AX=BAX=B,可以将向量X变化为B,矩阵范数就是来度量这个变化大小的。
这里简单地介绍以下几种向量范数的定义和含义
1、 L-P范数
与闵可夫斯基距离的定义一样,L-P范数不是一个范数,而是一组范数,其定义如下:
Lp=∑1nxpi−−−−√p,x=(x1,x2,⋯,xn)Lp=∑1nxipp,x=(x1,x2,⋯,xn)
根据P 的变化,范数也有着不同的变化,一个经典的有关P范数的变化图如下: 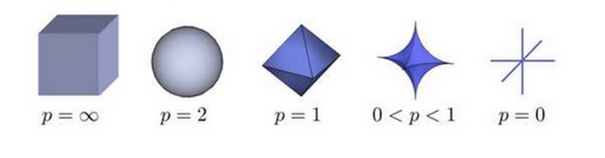
上图表示了p从无穷到0变化时,三维空间中到原点的距离(范数)为1的点构成的图形的变化情况。以常见的L-2范数(p=2)为例,此时的范数也即欧氏距离,空间中到原点的欧氏距离为1的点构成了一个球面。
实际上,在0≤p<1≤p<1时,Lp并不满足三角不等式的性质,也就不是严格意义下的范数。以p=0.5,二维坐标(1,4)、(4,1)、(1,9)为例,(1+4–√)−−−−−−−√0.5+(4–√+1)−−−−−−−√0.5<(1+9–√)−−−−−−−√0.5(1+4)0.5+(4+1)0.5<(1+9)0.5。因此这里的L-P范数只是一个概念上的宽泛说法。
2、L0范数
当P=0时,也就是L0范数,由上面可知,L0范数并不是一个真正的范数,它主要被用来度量向量中非零元素的个数。用上面的L-P定义可以得到的L-0的定义为:
||x||=∑1nx0i−−−−√0,x=(x1,x2,⋯,xn)||x||=∑1nxi00,x=(x1,x2,⋯,xn)
这里就有点问题了,我们知道非零元素的零次方为1,但零的零次方,非零数开零次方都是什么鬼,很不好说明L0的意义,所以在通常情况下,大家都用的是:
||x||0=||x||0=#(i|xi≠0)(i|xi≠0)
表示向量xx中非零元素的个数。
对于L0范数,其优化问题为:
min||x||0min||x||0
s.t. Ax=b
在实际应用中,由于L0范数本身不容易有一个好的数学表示形式,给出上面问题的形式化表示是一个很难的问题,故被人认为是一个NP难问题。所以在实际情况中,L0的最优问题会被放宽到L1或L2下的最优化。
3、L1范数
L1范数是我们经常见到的一种范数,它的定义如下:
||x||1=∑i|xi|||x||1=∑i|xi|
表示向量xx中非零元素的绝对值之和。
L1范数有很多的名字,例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference):
SAD(x1,x2)=∑i|x1i−x2i|SAD(x1,x2)=∑i|x1i−x2i|
对于L1范数,它的优化问题如下:
min||x||1min||x||1
s.t.Ax=bs.t.Ax=b
由于L1范数的天然性质,对L1优化的解是一个稀疏解,因此L1范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏,去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高体重等可能都是无用的,利用L1范数就可以过滤掉。
4、L2范数
L2范数是我们最常见最常用的范数了,我们用的最多的度量距离欧氏距离就是一种L2范数,它的定义如下:
||x||2=∑ix2i−−−−−√||x||2=∑ixi2
表示向量元素的平方和再开平方。
像L1范数一样,L2也可以度量两个向量间的差异,如平方差和(Sum of Squared Difference):
SSD(x1,x2)=∑i(x1i−x2i)2SSD(x1,x2)=∑i(x1i−x2i)2
对于L2范数,它的优化问题如下:
min||x||2min||x||2
s.t.Ax=bs.t.Ax=b
L2范数通常会被用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。
5、L-∞范数∞范数
当P=∞∞时,也就是L-∞∞范数,它主要被用来度量向量元素的最大值。用上面的L-P定义可以得到的L∞∞的定义为:
||x||∞=∑1nx∞i−−−−−√∞,x=(x1,x2,⋯,xn)||x||∞=∑1nxi∞∞,x=(x1,x2,⋯,xn)
与L0一样,在通常情况下,大家都用的是:
||x||∞=max(|xi|)||x||∞=max(|xi|)
来表示L∞