一篇自己都看不懂的树链剖分学习笔记

树链剖分是一个比较好理解的数据结构，码量不是很大（如果你发现你写的很多，那么一定是线段树的锅）

PS：树链剖分默认为重链剖分，长链剖分和实链剖分（LCT）以后有时间再写

One.树链剖分用来干啥

树链剖分的基本应用是对一段路径上或者一棵子树的点的点权进行修改，并且对路径或者子树内的点权进行查询操作。树链剖分本身的复杂度为$O(nlogn)$，但是因为它经常要与线段树、树状数组等$log$数据结构共用，所以一般需要用到树链剖分的问题的时间复杂度为$O(nlog^2n)$

Two.前置知识

会dfs序、会线段树，要求还是很低的

Three.理论

先约定几个符号：

$size_i$：以点$i$为根的子树的大小

$dfn_i$：点$i$在$dfs$时获得的序号（即点$i$的$dfs$序）

$dep_i$：点$i$的深度

$top_i$：等会儿解释

数据结构的名字是树链剖分，也就是把一棵树剖成一条一条的链进行维护。其中最讲究的还是如何剖链。

$For\,example$，对于下面这棵树，我们对它进行剖分

在树链剖分的模式下，我们标记每一个点与其$size$最大的儿子（称其为重儿子）的边（如果没有儿子就不管），因为这个儿子是最重的，所以称它为重边，而其他没有标记的边为轻边，如果有多个$size$同样最大的儿子，就随机标记一条。

如果将重边标红，那么上面的那棵树就会变成下面这样：

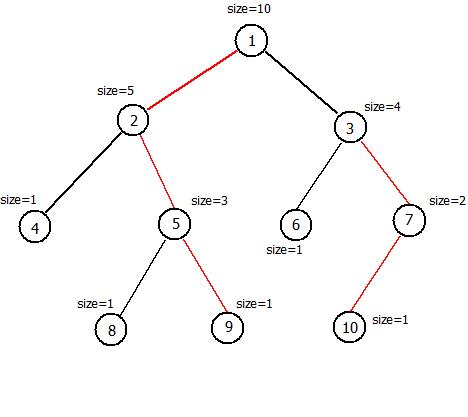
可以发现重边相连形成了一些重链（这棵树上有$2$条重链）

关于轻边和重链有一个很重要的性质：

每一个点到根所经过的轻边和重链的数量不超过$logn$条（其中$n$为点数）

证明：对于轻边，考虑子树大小。假如从$i$号点通过一条轻边跳到了其父亲$j$号点，那么意味着至少存在一个不为$i$的$j$的儿子$k$满足$size_k \geq size_i$，那么$size_j \geq size_i \times 2$，也就是说从$i$走到$j$，子树大小至少翻倍，那么经过$x$条轻边到达的点的子树大小至少为$2^x$，所以$2^x \leq n$，即$x \leq logn$。因为重链是被轻边分开的，所以重链的数量也不会超过$logn$条。

这一个结论意味着如果我们可以将重链上的操作变为$O(1)$或者$O(logn)$的话，时间复杂度就会十分优秀。

在区间修改之前，考虑一个问题：如何在树链剖分的模式下求$LCA$

考虑将每一个点所在的重链中深度最浅的点，也就是链顶$top$记下来，就像下面这样

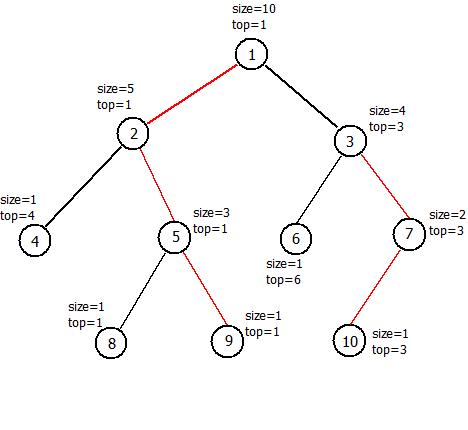
（这里手滑了，$top_8$应该等于$8$）

可以发现：我们可以通过$top\,O(1)$地跳一条重链了！那么根据上面的分析，我们求$LCA$的复杂度也就是$O(logn)$了，复杂度与倍增一致，但是树链剖分常数更小（因为实际上很难跳满$logn$条链）

总结一下求$x,y$两点$LCA$的操作步骤：

1、获得$top_x$和$top_y$

2、如果$top_x==top_y$转步骤5，否则转步骤3

3、如果$dep_{top_x}<dep_{top_y}$，交换$x$和$y$

4、令$x=fa_{top_x}$，跳过$x$所在的重链和重链顶的轻边，转步骤1

5、如果$dep_x<dep_y$，则$LCA(x,y)=x$，否则为$y$

不是很好理解的是步骤3，为什么要比较$top$的$dep$的大小而不是本身的$dep$的大小？留给读者自证

会跳LCA了，接下来考虑路径和子树的修改。

对于树上的区间修改我们常用$DFS$序+区间修改数据结构进行配合，在树链剖分中也是一样的，但是因为我们需要优化重链上的修改，所以$DFS$的顺序十分重要。

我们每一次$DFS$到一个点，优先向其重儿子$DFS$，这样可以得到一个特别的$dfn$序：

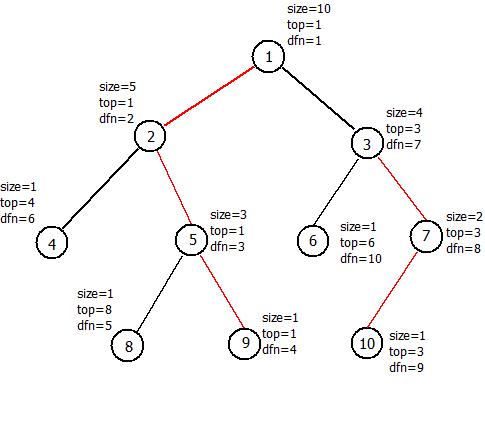
可以发现一条重链上的$dfn$是连续的，这意味着我们在对一条路径做修改的时候，在上面求两点$LCA$的过程中对跳过的重链的部分进行区间修改就可以了，查询同理。使用线段树、树状数组等数据结构可以对这一些修改和查询进行维护。

而子树的$dfn$序显然也是连续的。

那么我们最重要的修改和查询问题就解决了o(*￣▽￣*)ブ

Four.实现的一些细节

一般树链剖分的实现是两个$dfs$：

第一个$dfs$处理$dep$、$fa$、$size$和重儿子

第二个$dfs$处理$top$和$dfn$

Five.一个例题

例题当然要是Luogu的树链剖分模板题

其实操作就是上面的操作qwq

  1 #include<bits/stdc++.h>
  2 #define MAXN 100001 
  3 using namespace std;
  4 inline int read(){
  5     int a = 0;
  6     char c = getchar();
  7     while(!isdigit(c))
  8         c = getchar();
  9     while(isdigit(c)){
 10         a = (a << 3) + (a << 1) + (c ^ '0');
 11         c = getchar();
 12     }
 13     return a;
 14 }
 15 
 16 int forOutput[12];
 17 inline void print(int a){
 18     int dirN = 0;
 19     while(a){
 20         forOutput[dirN++] = a % 10;
 21         a /= 10;
 22     }
 23     if(dirN == 0)
 24         putchar('0');
 25     while(dirN)
 26         putchar('0' + forOutput[--dirN]);
 27     putchar('\n');
 28 }
 29 
 30 struct node{
 31     int l , r , sum , mark;
 32 }SegTree[MAXN << 2];
 33 struct Edge{
 34     int end , upEd;
 35 }Ed[MAXN << 1];
 36 int N , M , R , P , ts , cntEd;
 37 int fa[MAXN] , size[MAXN] , son[MAXN] , ind[MAXN] , rk[MAXN] , depth[MAXN] , top[MAXN] , val[MAXN] , head[MAXN] , maxInd[MAXN];
 38 
 39 inline int max(int a , int b){
 40     return a > b ? a : b;
 41 }
 42 
 43 //加边
 44 inline void addEd(int a , int b){
 45     Ed[++cntEd].end = b;
 46     Ed[cntEd].upEd = head[a];
 47     head[a] = cntEd;
 48 }
 49 
 50 //第一个dfs，处理size、son、fa和dep
 51 void dfs1(int dir , int dep , int father){
 52     depth[dir] = dep;
 53     fa[dir] = father;
 54     size[dir] = 1;
 55     for(int i = head[dir] ; i ; i = Ed[i].upEd)
 56         if(Ed[i].end != father){
 57             dfs1(Ed[i].end , dep + 1 , dir);
 58             size[dir] += size[Ed[i].end];
 59             if(size[son[dir]] < size[Ed[i].end])
 60                 son[dir] = Ed[i].end;
 61         }
 62 }
 63 
 64 //第二个dfs，处理top和ind
 65 //注意到那个rk了吗?rk[i]表示的是dfs序为i的点在原树中的编号，这样在线段树的初始化部分就可以直接带入点权了。
 66 void dfs2(int dir , int t){
 67     top[dir] = t;
 68     maxInd[dir] = ind[dir] = ++ts;
 69     rk[ts] = dir;
 70     if(!son[dir])
 71         return;
 72     dfs2(son[dir] , t);
 73     maxInd[dir] = max(maxInd[dir] , maxInd[son[dir]]);
 74     for(int i = head[dir] ; i ; i = Ed[i].upEd)
 75         if(Ed[i].end != son[dir] && Ed[i].end != fa[dir]){
 76             dfs2(Ed[i].end , Ed[i].end);
 77             maxInd[dir] = max(maxInd[dir] , maxInd[Ed[i].end]);
 78         }
 79 }
 80 
 81 //线段树更新信息
 82 inline void pushup(int dir){
 83     SegTree[dir].sum = (SegTree[dir << 1].sum + SegTree[dir << 1 | 1].sum) % P;
 84 }
 85 
 86 //线段树下放标记
 87 inline void pushdown(int dir){
 88     if(SegTree[dir].mark){
 89         SegTree[dir << 1].sum = (SegTree[dir << 1].sum + (SegTree[dir << 1].r - SegTree[dir << 1].l + 1) * SegTree[dir].mark) % P;
 90         SegTree[dir << 1 | 1].sum = (SegTree[dir << 1 | 1].sum + (SegTree[dir << 1 | 1].r - SegTree[dir << 1 | 1].l + 1) * SegTree[dir].mark) % P;
 91         SegTree[dir << 1].mark = (SegTree[dir << 1].mark + SegTree[dir].mark) % P;
 92         SegTree[dir << 1 | 1].mark = (SegTree[dir << 1 | 1].mark + SegTree[dir].mark) % P;
 93         SegTree[dir].mark = 0;
 94     }
 95 }
 96 
 97 //线段树初始化
 98 void init(int dir , int l , int r){
 99     SegTree[dir].l = l;
100     SegTree[dir].r = r;
101     if(l == r)
102     //rk在这里起作用！
103         SegTree[dir].sum = val[rk[l]] % P;
104     else{
105         init(dir << 1 , l , l + r >> 1);
106         init(dir << 1 | 1 , (l + r >> 1) + 1 , r);
107         pushup(dir);
108     }
109 }
110 
111 //线段树修改
112 void change(int dir , int l , int r , int mark){
113     if(SegTree[dir].l >= l && SegTree[dir].r <= r){
114         SegTree[dir].mark = (SegTree[dir].mark + mark) % P;
115         SegTree[dir].sum = (SegTree[dir].sum + (SegTree[dir].r - SegTree[dir].l + 1) * mark) % P;
116         return;
117     }
118     pushdown(dir);
119     if(l <= SegTree[dir].l + SegTree[dir].r >> 1)
120         change(dir << 1 , l , r , mark);
121     if(r > SegTree[dir].l + SegTree[dir].r >> 1)
122         change(dir << 1 | 1 , l , r , mark);
123     pushup(dir);
124 }
125 
126 //线段树查询和
127 int getSum(int dir , int l , int r){
128     if(SegTree[dir].l >= l && SegTree[dir].r <= r)
129         return SegTree[dir].sum;
130     pushdown(dir);
131     int sum = 0;
132     if(l <= SegTree[dir].l + SegTree[dir].r >> 1)
133         sum = (sum + getSum(dir << 1 , l , r)) % P;
134     if(r > SegTree[dir].l + SegTree[dir].r >> 1)
135         sum = (sum + getSum(dir << 1 | 1 , l , r)) % P;
136     return sum;
137 }
138 
139 //边跳边修改的路径操作
140 inline void work1(int x , int y , int z){
141     int fx = top[x] , fy = top[y];
142     while(fx != fy){
143         if(depth[fx] >= depth[fy]){
144             //将跳过的重链进行修改，下同
145             change(1 , ind[fx] , ind[x] , z);
146             x = fa[fx];
147             fx = top[x];
148         }
149         else{
150             change(1 , ind[fy] , ind[y] , z);
151             y = fa[fy];
152             fy = top[y];
153         }
154     }
155     //将最后一段修改
156     if(ind[x] <= ind[y])
157         change(1 , ind[x] , ind[y] , z);
158     else
159         change(1 , ind[y] , ind[x] , z);
160 }
161 
162 //边跳边算答案
163 inline int work2(int x , int y){
164     int fx = top[x] , fy = top[y] , sum = 0;
165     while(fx != fy){
166         if(depth[fx] >= depth[fy]){
167             //边跳边加入答案
168             sum = (sum + getSum(1 , ind[fx] , ind[x])) % P;
169             x = fa[fx];
170             fx = top[x];
171         }
172         else{
173             sum = (sum + getSum(1 , ind[fy] , ind[y])) % P;
174             y = fa[fy];
175             fy = top[y];
176         }
177     }
178     //将最后一段算入答案
179     if(ind[x] <= ind[y])
180         sum = (sum + getSum(1 , ind[x] , ind[y])) % P;
181     else
182         sum = (sum + getSum(1 , ind[y] , ind[x])) % P;
183     return sum;
184 }
185 
186 //子树修改与查询
187 void work3(int x , int z){
188     change(1 , ind[x] , maxInd[x] , z);
189 }
190 
191 int work4(int x){
192     return getSum(1 , ind[x] , maxInd[x]);
193 }
194 
195 int main(){
196     N = read();
197     M = read();
198     R = read();
199     P = read();
200     for(int i = 1 ; i <= N ; i++)
201         val[i] = read();
202     for(int i = 1 ; i < N ; i++){
203         int a = read() , b = read();
204         addEd(a , b);
205         addEd(b , a);
206     }
207     dfs1(R , 1 , 0);
208     dfs2(R , R);
209     init(1 , 1 , N);
210     while(M--){
211         int a = read() , b = read() , c , d;
212         switch(a){
213             case 1:
214                 c = read();
215                 d = read();
216                 work1(b , c , d);
217                 break;
218             case 2:
219                 c = read();
220                 print(work2(b , c));
221                 break;
222             case 3:
223                 c = read();
224                 work3(b , c);
225                 break;
226             case 4:
227                 print(work4(b));
228         }
229     }
230     return 0;
231 }