机器学习 --- 拉格朗日乘子法和KTT条件

本篇文章主要为之后的支持向量机打下数学基础

一、拉格朗日乘子法的目的

拉格朗日乘子法将原始的约束问题转换成求解无约束优化问题。

对形如：

$\min \limits_{x\epsilon R^{n}} \ f(x)$

$s.t \qquad h_{i}=0,\ i=1,2,...,k$

$\qquad \quad \ g_{j}(x) \leq0,\ j=1,2,...,l$

通过拉格朗日乘子法转化成：

$\min \limits_{x} \max \limits_{\lambda,\mu}L(x,\lambda,\mu)$

通俗地说就是转换目标函数，把约束条件去掉。

二、等式约束条件下的拉格朗日乘子法

在约束条件是等式的情况下，引用深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件对拉格朗日乘子法的直观理解。

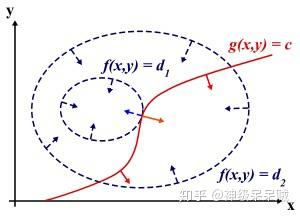
设想我们的目标函数 $z=f(x)$ ， $z$ 取不同的值，相当于投影在 $x$ 构成的平面（曲面）上，即成为等高线。如下图所示，目标函数是 $f(x,y)$ ，这里 $x$ 是标量，虚线是等高线。假设约束函数 $g(x)=0$ ,在 $x$ 构成的平面或者曲面上是一条曲线。现假设 $g(x)$ 与等高线相交，这里的交点就是既满足了等式约束条件和目标函数可行域的值，但一定不是最优值。因为相交就意味着还存在其他的等高线在该条等高线的内部或外部，使得新的等交线与目标函数的交点的值更大或者更小。只有等高线与目标函数的曲线相切的时候，可能取得最优值，如下图所示，即等高线和目标函数得曲线在该点得法向量必须有相同得方向

有上面的理解，设最优点 $x^{*}$ ，则有 $\lambda\ne0$ 使得：

$\nabla f(x^{*})=\lambda\ \nabla g(x^{*}) \qquad \qquad (1)$

在约束条件是等式的情况下，定义拉格朗日函数：

$L(x,\lambda)=f(x)+\lambda\ g(x) \qquad \qquad (2)$

观察(2)式可以发现对 $x$ 的偏导数并置零，得到(1)式。因此可以将有等式约束的优化问题，通过(2)式改写成无约束优化问题。

三、不等式约束下的KKT条件

现在考虑含有不等式约束的优化条件。

当不等式约束 $g(x)\leq 0$ ，此时的最优点 $x^{*}$ 要么在 $g(x)<0$ 区域内，要么在 $g(x)=0$ 上。对于 $g(x)<0$ 的情形下，约束条件不起作用，此时是一个无约束的优化问题，可以直接通过 $\nabla f(x)=0$ 来获取最优点。对于 $g(x)=0$ 的情况下，这就相当于一个等式约束，但此时的 $\nabla f(x^{*})$ 方向与 $\nabla g(x^{*})$ 的方向相反，否则将会突破 $g(x)<0$ 的约束。即存在 $\lambda >0$ 使得 $\nabla f(x^{*})+\lambda \ \nabla g(x^{*})=0$ 。所以在 $g(x)\leq0$ 情况下，考虑之前提到的两种情况，推导出拉格朗日函数的KKT条件：

$\left\{ \begin{aligned} &g(x)\leq0 \\ & \lambda\geq0 \\ & \lambda \ g(x)=0\ \end{aligned} \right.$

四、对偶问题

在满足KKT的条件下后，通过求解对偶问题来替代求解的原问题，这样可以避免求解复杂的原问题。

在这种情况下，将目标函数，等式约束，不等式约束写成一个方程式，若有 $k$ 个等式约束和 $l$ 个不等式约束，则定义拉格朗日函数:

$L(x,\lambda,\mu)=f(x)+ \sum_{i=1}^{k}{\mu_{i} h_{i}(x)} + \sum_{j=1}^{l}{\lambda_{j} g_{j}(x)}\qquad \qquad(3)$

回顾目标函数，需要 $\min \limits_{x\epsilon R^{n}} \ f(x)$ ，由拉格朗日函数，在KKT条件下， $\max \limits_{\lambda,\mu} \ L(x,\lambda,\mu)$ 就是 $f(x)$ 这是因为，在KKT条件下，在 $h(x)=0$ ， $\lambda \ g(x)=0$ 时。观察(3)式，此时 $\max \limits_{\lambda,\mu} \ L(x,\lambda,\mu)$ 等价于 $f(x)$ 。

因此在满足约束条件的情况下，原问题的最优值 $p^{*}$ ：

$p^{*}=\min \limits_{x} \theta_{P}(x)=\min \limits_{x}\max \limits_{\lambda,\mu} \ L(x,\lambda,\mu)$

则对偶问题的最优值 $d^{*}$ ：

$d^{*}=\max \limits_{\lambda,\mu} \theta_{D}(\lambda,\mu)=\max \limits_{\lambda,\mu} \min \limits_{x} L(x,\lambda,\mu)$

形式上观察，原问题先固定 $x$ ，优化参数 $\lambda,\mu$ ，再优化出 $x$ ，而对偶问题则是先固定 $\lambda,\mu$ ，优化参数 $x$ ，再优化出 $\lambda,\mu$ 。

分别求出原始问题的最优值 $p^{*}$ 和对偶问题的最优值 $d^{*}$ 后，二者间的关系有：

$d^{*}\leq p^{*}$

证明：
$\theta_{D}(\lambda,\mu)=\min \limits_{x}L(x,\lambda,\mu)\leq L(x,\lambda,\mu)\leq \max \limits_{\lambda,\mu}L(x,\lambda,\mu)=\theta_{P}(x)$
$\theta_{D}(\lambda,\mu)\leq \theta_{P}(x)$
又因为原始问题与对偶问题都有最优值:
$\max \limits_{\lambda,\mu} \theta_{D}(\lambda,\mu) \leq \min \limits_{x} \theta_{P}(x)$
所以 $d^{*}\leq p^{*}$