模拟退火算法理论+Python解决函数极值+C++实现解决TSP问题

简述

算法设计课这周的作业：
赶紧写了先，不然搞不完了。

文章目录

简述
算法理论部分

变量简单分析
从状态转移概率到状态概率
推导
理解当温度收敛到接近0的时候，收敛到结果
理论部分的后记

python实现

python实现模拟退火解极值

C++实现解函数值问题
TSP问题求解

代码详细解释

定义了两个宏，主要是为了加速运算
定义全局变量
函数解释

算法理论部分

用粒子的排列或相应的能量表示物体所处的状态，在温度T下，物体(系统)所处的状态具有一定的随机性。主流趋势是系统向能量较低的状态发展，但粒子的不规则热运动妨碍系统准确落入低能状态。

简单来说就是，在温度T下，

有两种可能

$f(x_i) \ge f(x_j)$ ，那没得说有更好的肯定选更好的。
$f(x_i) < f(x_j)$ ，这个时候我们也有一定的概率选这个。

概率为

$P(X_{i\rightarrow j}) = e^{\frac{f(x_i) - f(x_j)}{KT}}$

其中K为玻尔兹曼常数（在这个算法上，我们经常使用数值1代替这个）

$K>0$ ，一般设置为 $K=1$
$T > 0$ ，我们在递减的过程中，终止的T，一般认为是 $T = 1$

变量简单分析

不难看出，随着T下降，这个状态转移的概率是下降的。

原因： $f(x_i) - f(x_j) < 0$

物理上解释：

因为之前的这个转移概率，认为是，在高温情况下，分子可能会产生较为不稳定的随机运动。且温度越高，这个分子不规则运动的可能是更大的。这是在模拟这个过程。
所以，我们称这个算法为，模拟退火算法

从状态转移概率到状态概率

这个分析过程，其实是类似于推理马尔可夫链的过程。

之前给给出的 $P(X_{i\rightarrow j})$ 其实是条件概率。

我们假设第n个状态为 $X_i$ ，那么现在就是考虑下一个状态的概率。

$P(s_{n+1} = X_j| s_n =X_i) = P(X_{i\rightarrow j})= e^{\frac{f(x_i) - f(x_j)}{KT}}$

我们用 $s_n$ ，表示第n个状态。

用条件概率公式得到

$P(s_{n+1} = X_j| s_n =X_i) = \frac{P(s_{n+1} = X_j, s_n =X_i)}{P(s_n =X_i)}$

$P(s_{n+1} = X_j, s_n =X_i) = P(s_n =X_i)* P(s_{n+1} = X_j| s_n =X_i)$
$P(s_{n+1} = X_j) = \sum_{i}{P(s_n =X_i)* P(s_{n+1} = X_j| s_n =X_i)}$

而解这个过程，就用到了以前解马尔科夫过程的方法，这里我需要假设一个均衡态，在这种状态下，经过任意次状态转移之后，整个模型的概率保持一致。

得到结果是

$P_i(T) = \frac{e^{\frac{-f(x_i)}{KT}}}{Z_T}$

$Z_T$ 只是一个归一化的因子而已，就是把所有的这样的分子的数值求个和。使得概率和为一而已。

这个分布称之为 Boltzmann分布。

推导

$P_i(T)-P_j(T) = \frac{e^{\frac{-f(i)}{KT}}}{Z_T}(1-e^{-\frac{f(j)-f(i)}{KT}})$

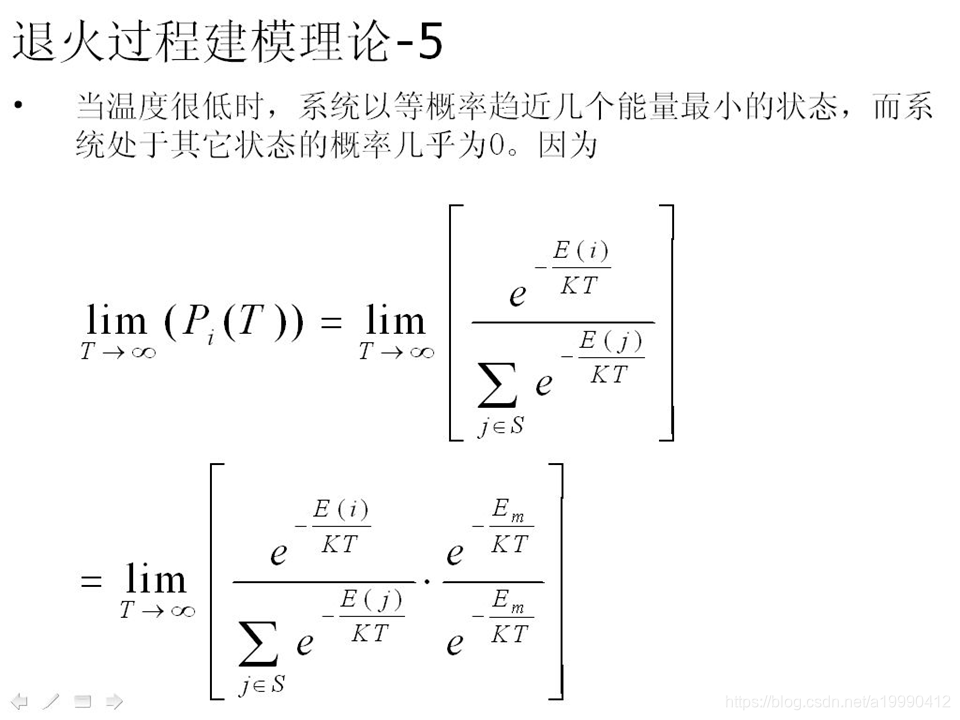
在这里插入图片描述

理解当温度收敛到接近0的时候，收敛到结果

其实只需要理解下面这个函数的导数就可以了

$e^{-\frac{E(i)}{KT}}$
关于T求导。

$e^{-\frac{E(i)}{KT}}*\frac{E(i)}{kT^2}$

那么，这就是这个变量关于T的变化导数。再考虑关于函数值 $E(i)$

这个函数是关于 $E(i)$ 的单调减函数。 $E(i)>0$ 的情况下。

所以说，函数值稍微小的数值所对应的状态概率，受到T的减小而导致的减小的幅度，其实是较为小的。
那么当T趋于0的时候，就可以得到，状态概率，会集中在函数值较为小的数值点上（数值小的点的概率大）

也就是说，当模拟退火，温度越低，越有可能收敛到正确解。而且，这是收敛的。

理论部分的后记

这里，我们证明了，当温度越小，越会收敛到正确解。这只是在理论上的证明。但是我们都知道，当T趋于0，但是特别小的时候，作为分母时，这个精度就会变得非常低了（计算机上是离散的）。

所以，为了简单，我们一般设置T到1就截止了。

python实现

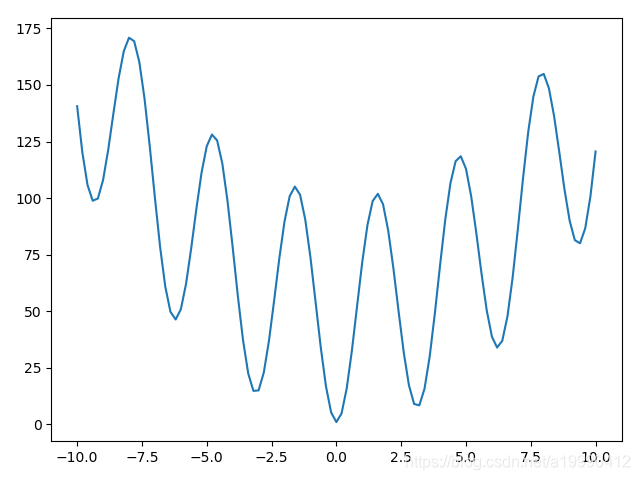
先尝试解决下面的这个图

在这里插入图片描述

import numpy as np
import matplotlib.pyplot as plt

f = lambda x: (x - 1) ** 2 + x + 100 * np.sin(x)**2
x = np.linspace(-10., 10, 101)
plt.plot(x, f(x))
plt.show()

python实现模拟退火解极值

先在这个区间上随机生成一个起始点
每次在给定点的一个邻近区域（自己设置），找到一个新的点。
然后这两个点做比较。通过概率模拟来确定是否发生位置迁移。
直到温度下降到一定的数值。

import numpy as np
import matplotlib.pyplot as plt

f = lambda x: (x - 1) ** 2 + x + 100 * np.sin(x) ** 2
x = np.linspace(-10., 10, 101)
plt.plot(x, f(x))

T = 1000  # 起始温度
alpha = 0.9  # T_{k+1} = alpha * T_k方式更新温度
limitedT = 1.  # 最小值的T
iterTime = 1000  # 每个温度下迭代的次数
sigmaX = 3  # 每次的搜索半径
K = 1  # 系数K
X = 20 * np.random.rand() - 10
Y = f(X)
while T > limitedT:
    for i in range(iterTime):
        xnew = X + sigmaX * (2 * np.random.rand() - 1)
        if xnew <= 10. and xnew >= -10.:
            fnew = f(xnew)
            if fnew < Y:
                Y = fnew
                X = xnew
            else:
                res = Y-fnew
                p = np.exp(res / (K * T))
                if np.random.rand() < p:
                    X = xnew
                    Y = fnew
    T *= alpha
print(X, Y)
plt.plot(X, Y, '*r')
plt.show()

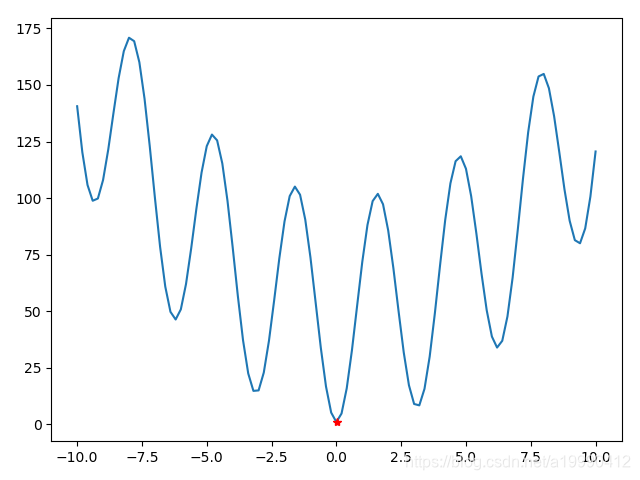
在这里插入图片描述

基本上准确~

C++实现解函数值问题

对于上面一个问题的C++解法
但是C++的精度似乎没有Python的好。这个可以适当调节参数来获得更高的精度，反正C++的速度也快很多。

#include <iostream>
#include <cmath>
#include <ctime>
using namespace std;
#define FUN(x) ((x-1)*(x-1) + x + 100 * sin(x) * sin(x))
#define RAND() ( (double)rand()  / double(RAND_MAX))

int main() {
	srand((unsigned)time(NULL));
	double T = 1000;  // 起始温度
	double alpha = 0.99;  // T_{ k + 1 } = alpha * T_k方式更新温度
	double limitedT = 1;  // 最小值的T
	int iterTime = 1000; // 每个温度下迭代的次数
	double sigmaX = 3; // 每次的搜索半径
	double K = 1; // 系数K
	double X = 20 * RAND() - 10;
	double Y = FUN(X);
	double xnew, ynew, rest, p;
	while (T > limitedT) {
		for (int i = 0; i < iterTime; ++i) {
			xnew = X + sigmaX * (2 * RAND() - 1);
			if (xnew >= -10. && xnew <= 10) {
				ynew = FUN(xnew);
				if (ynew <= Y) {
					X = xnew;
					Y = ynew;
				}
				else {
					rest = Y-ynew;
					p = exp(rest / (K*T));
					if (RAND() < p) {
						X = xnew;
						Y = ynew;
					}
				}
			}
		}
		T *= alpha;
	}
	cout << X << " " << Y << endl;
	system("pause");
}

TSP问题求解

代码详细解释

定义了两个宏，主要是为了加速运算

第一个是**RAND(b,e)**生成在 $[b,e)$ 这个区间上的整数
第二个是**RANDFLOAT()**是为了生成(0,1)之间的数。

定义全局变量

double **Mat;
int *Path, *tempPath;
double Value, tempValue;
int N = 0;

Mat是来存储距离矩阵的
Path存储路径
Value存储路劲所对应的函数。这里考虑的是具体的数值
N表示有多少个点
所有前面加了temp都表示临时变量。

函数解释

double CalValue(int *p) 函数用于给输入的路劲下，求对应的value值。
void refresh() 将temp的数组和具体数值恢复。为了下一次的考虑
void change() 覆盖掉原来的路劲。进行存储。
void initialPath() 初始化路径。并算出初始值。

#include <iostream>
#include <cmath>
#include <ctime>
#include <fstream>
using namespace std;
#define RAND(b, e) (rand() % (e-b) + b)
// 左闭右开
#define RANDFLOAT() ((double)rand() / double(RAND_MAX))
// 0-1浮点数

double **Mat;
int *Path, *tempPath;
double Value, tempValue;
int N = 0;


double CalValue(int *p) {
	double t = 0;
	for (int i = 1; i < N; ++i) {
		t += Mat[p[i - 1]][p[i]];
	}
	t += Mat[p[N - 1]][0];
	return t;
}

// 将temp重置为path
void refresh() {
	for (int i = 0; i < N; ++i) {
		tempPath[i] = Path[i];
	}
	tempValue = Value;
}

// 覆盖修改Path
void change() {
	for (int i = 0; i < N; ++i) {
		Path[i] = tempPath[i];
	}
	Value = tempValue;
}

void initialPath() {
	for (int i = 0; i < N; ++i) {
		Path[i] = i;
	}
	// Path[i]表示路上第i个点的标记为Path[i]
	// Path[0] = 0
	int tx,t;
	for (int i = 1; i < N-1; ++i) {
		tx = RAND(i, N);
		if (tx != i) { // swap
			t = Path[i];
			Path[i] = Path[tx];
			Path[tx] = t;
		}
	}
	Value = CalValue(Path);
}


int main() {
	srand((unsigned)time(NULL));
	ifstream cin("data.txt");
	
	cin >> N;
	// initialize
	Mat = new double *[N];
	for (int i = 0; i < N; ++i)
		Mat[i] = new double[N];
	for (int i = 0; i < N; ++i) {
		for (int j = 0; j < N; ++j) {
			cin >> Mat[i][j];
		}
	}
	Path = new int[N];
	tempPath = new int[N];

	double T = 1000;  // 起始温度
	double alpha = 0.99;  // T_{ k + 1 } = alpha * T_k方式更新温度
	double limitedT = 1e-9;  // 最小值的T
	int iterTime = 1000; // 每个温度下迭代的次数
	double K = 1; // 系数K
	double p = 0;
	initialPath();
	int tx, ty, t;
	while (T >= limitedT) {
		for (int i = 0; i < iterTime; ++i) {
			// 任意交换两点的顺序
			refresh();
			tx = RAND(1, N);
			ty = RAND(1, N);
			if (tx != ty) {
				t = tempPath[tx];
				tempPath[tx] = tempPath[ty];
				tempPath[ty] = t;
				tempValue = CalValue(tempPath);

				if (tempValue <= Value) {
					change();
				}
				else {
					p = exp((Value-tempValue) / (K*T));
					if (RANDFLOAT() < p) { change(); }
				}
			}
		}
		T *= alpha;
	}
	cout << "Value:" << Value << endl;
	for (int i = 0; i < N; ++i) {
		cout << Path[i] << " -> ";
	}
	cout << 0 << endl;
	// release
	delete[]tempPath;
	delete[] Path;
	for (int i = 0; i < N; ++i)
		delete[] Mat[i];
	delete[] Mat;
	system("pause");
}