线性筛阶乘的逆元

版权声明：转载注明下出处就行了。 https://blog.csdn.net/LJD201724114126/article/details/83781619

typedef long long LL;

const LL mod=1e9+7;
const int maxn=3e5+10;
const int N=3e5;

int jie[maxn],ni[maxn];
void init()
{
    jie[0]=jie[1]=1;

    for(int i=2;i<=N;i++)
        jie[i]=1LL*jie[i-1]*i%mod; ///前i项的阶乘

    ni[N]=pow(jie[N],mod-2); ///逆元，调用pow函数时应 用LL

    for(int i=N;i>=1;i--) ///线性筛逆元
    {
        ni[i-1]=1LL*ni[i]*i%mod;
    }
}

ni[N]=(1*2*3*...*N)^(mod-2)=(1*2*3*...*(N-1))^(mod-2)*N^(mod-2)

ni[N-1]=(1*2*3*...*(N-1))^(mod-2)=ni[N]/(N^(mod-2),

我们由费马小定理可知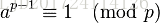，  （a不是p的倍数，也就是p不能整除a，那么p是质数，就一定满足）。

 , 变形得 a*a^(p-2)≡1(mod p)，答案已经很明显了:若a,p互质,a^(p-2)的逆元就是a，即N^(mod-2)的逆元就是N，

故ni[N-1]=ni[N]*N。