一、直接采样
直接采样的思想是,通过对均匀分布采样,实现对任意分布的采样。因为均匀分布采样好猜,我们想要的分布采样不好采,那就采取一定的策略通过简单采取求复杂采样。
假设y服从某项分布p(y),其累积分布函数CDF为h(y),有样本z~Uniform(0,1),我们令 z = h(y),即 y = h(z)^(-1),结果y即为对分布p(y)的采样。

直接采样的核心思想在与CDF以及逆变换的应用。在原分布p(y)中,如果某个区域[a, b]的分布较多,然后对应在CDF曲线中,[h(a), h(b)]的曲线斜率便较大。那么,经过逆变换之后,对y轴(z)进行均匀分布采样时,分布多的部分(占据y轴部分多)对应抽样得到的概率便更大,
局限性
实际中,所有采样的分布都较为复杂,CDF的求解和反函数的求解都不太可行。
二、拒绝采样
拒绝采样是由一个易于采样的分布出发,为一个难以直接采样的分布产生采样样本的通用算法。既然 p(x) 太复杂在程序中没法直接采样,那么便一个可抽样的分布 q(x) 比如高斯分布,然后按照一定的方法拒绝某些样本,达到接近 p(x) 分布的目的。
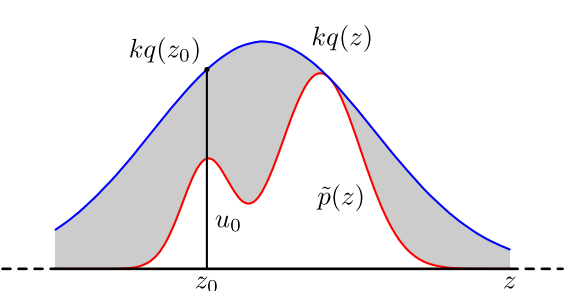
计算步骤
设定一个方便抽样的函数 q(x),以及一个常量 k,使得 p(x) 总在 k*q(x) 的下方。(参考上图)
- x 轴方向:从 q(x) 分布抽样得到 a;
- y 轴方向:从均匀分布(0, k*q(a)) 中抽样得到 u;
- 如果刚好落到灰色区域: u > p(a), 拒绝, 否则接受这次抽样;
- 重复以上过程。
计算步骤(BN)
- 根据网络指定的先验概率分布生成采样样本;
- 拒绝所有与证据不匹配的样本;
- 在剩余样本中对事件X=x的出现频繁程度计数从而得到估计概率、
局限性
- 拒绝了太多的样本!随着证据变量个数的增多,与证据e相一致的样本在所有样本中所占的比例呈指数级下降,所以对于复杂问题这种方法是完全不可用的。
- 难以找到合适的k*q(a),接受概率可能会很低。
三、重要性采样(似然加权)
重要性采样主要是用于求一个复杂分布p(x)的均值,最后并没有得到样本。
重要性采样的思想是借助一个易于采样的简单分布q(x),对这个简单分布q(x)所得到的样本全部接受。但是以此得到的样本肯定不满足分布p(x),因此需要对每一个样本附加相应的重要性权重。在重要性采样中,以p(x0)/q(x0)的值作为每个样本的权重。这样,当样本和分布p(x)相近时,对应的权重大;与分布p(x)相差过多时,对应的权重小。这个方法采样得到的是带有重要性权重的服从q(z)分布的样本,这个权重乘以样本之后的结果其实就是服从p(z)分布的。

通过上述公式,我们可以知道重要性采样可以用于近似复杂分布的均值。
四、吉布斯采样
假设有一个例子:E:吃饭、学习、打球;时间T:上午、下午、晚上;天气W:晴朗、刮风、下雨。样本(E,T,W)满足一定的概率分布。现要对其进行采样,如:打球+下午+晴朗。
问题是我们不知道p(E,T,W),或者说,不知道三件事的联合分布。当然,如果知道的话,就没有必要用吉布斯采样了。但是,我们知道三件事的条件分布。也就是说,p(E|T,W), p(T|E,W), p(W|E,T)。现在要做的就是通过这三个已知的条件分布,再用Gibbs sampling的方法,得到联合分布。
具体方法:首先随便初始化一个组合,i.e. 学习+晚上+刮风,然后依条件概率改变其中的一个变量。具体说,假设我们知道晚上+刮风,我们给E生成一个变量,比如,学习→吃饭。我们再依条件概率改下一个变量,根据学习+刮风,把晚上变成上午。类似地,把刮风变成刮风(当然可以变成相同的变量)。这样学习+晚上+刮风→吃饭+上午+刮风。同样的方法,得到一个序列,每个单元包含三个变量,也就是一个马尔可夫链。然后跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取1个)。这样sample到的单元,是逼近联合分布的。
五、蓄水池采样
蓄水池抽样(Reservoir Sampling ),即能够在o(n)时间内对n个数据进行等概率随机抽取,例如:从1000个数据中等概率随机抽取出100个。另外,如果数据集合的量特别大或者还在增长(相当于未知数据集合总量),该算法依然可以等概率抽样。
算法步骤:
- 先选取数据流中的前k个元素,保存在集合A中;
- 从第j(k + 1 <= j <= n)个元素开始,每次先以概率p = k/j选择是否让第j个元素留下。若j被选中,则从A中随机选择一个元素并用该元素j替换它;否则直接淘汰该元素;
- 重复步骤2直到结束,最后集合A中剩下的就是保证随机抽取的k个元素。