Pessimistic Error Pruning example of C4.5

This example is from 《An Empirical Comparison of Pruning Methods
for Decision Tree Induction》
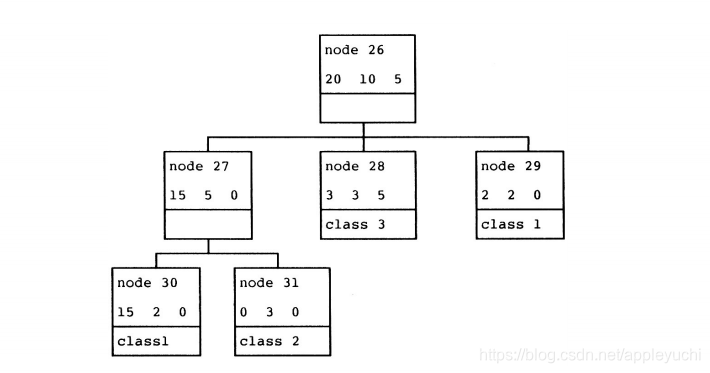
在这里插入图片描述
How to read these node and leaves?
For example:
node 30:
15 are classified as “class1”
2 are mis-classified as “class1”
you can reduce the rest nodes or leaves from above

criterion :
$n'(T_t)+SE(n'(Tt))<n'(t)①$
where
$SE(n'(Tt))=\sqrt{\frac{n'(T_t)·（N(t)-n'(T_t)）}{N(t)}}$
Be short :
Errors when unpruned<Errors after pruned

when ① is satisfied ,the current tree remains,
otherwise, it will be pruned.

The principle why above Algorithm always take effect
B(n,p)->N( np,np(1-p) )
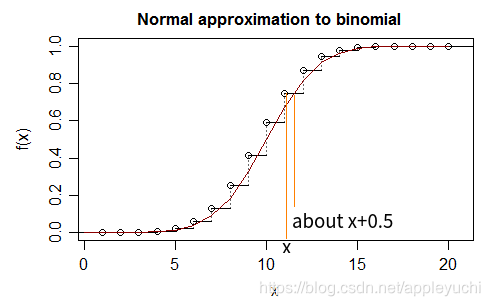
在这里插入图片描述
Picture Reference
:https://stats.stackexchange.com/questions/213966/why-does-the-continuity-correction-say-the-normal-approximation-to-the-binomia/213995

when in reverse,we set a continuity corretion for binomial distribution:
we use “x+0.5” to make these two curse closer(of course this is not accurate enough)，then you can use theory of Normal distribution with x+0.5
of course 0.5 is not rigorous,here is just approximation

Why the standard error occur in the criterion?
$n'(T_t)+SE(n'(Tt))<n'(t)$
$<=>n'(T_t)+\sqrt{\frac{n'(T_t)·（N(t)-n'(T_t)）}{N(t)}}<n'(t)$
Let’s see an example:
$Y=X_1+X_2+X_3+X_4$
$X_i$ will fluctuate and Y will fluctuate(I mean they are all variables,Not Constant).
then ,when does Y reach maximum?
Now if we have 4 values Y ever have produced.
1,2,1,1 ②
then average Y̅= $\frac{1}{4}(1+2+1+1)=1.25$
Standard Deviation= $\sqrt{\frac{1}{4}\{(1-1.25)^2+(2-1.25)^2+(1-1.25)^2+(1-1.25)^2\}}$ =0.43
so when
Y̅+Standard Deviation=1.25+0.43=1.68≈2.0

Conclusion 1：
All above means that when Y̅+Standard Deviation,we’ll get a value nearest to the maximum in②
------------------------------------------
Let’s come back to Errors we focus just now:
regard Y as the total number of Errors of un-pruned Tree:
Assume（Such Assumption is of course Not rigorous～！）:
Y̅= $n'(T_t)$
$X_i$ :Error number of the $i_{th}$ leaf
Standard Deviation: $SE(n'(Tt))$

just like the conclusion 1:
$n'(T_t)+SE(n'(Tt))$ means that:
we’ll get a value nearest to the maximum number among possible values of “errors of un-pruned tree”.
Attention please that we assume “errors of un-pruned tree” as a variable,Not constant,
which is used to get the " maximum possible error numbers".
The reason why we call it"pessimistic" is just from $SE(n'(Tt))$
this item means:“pessimistic Error counts”

Note:
There’s a complaint from part2.2.5 of《An Empirical Comparison of Pruning Methods for Decision Tree Induction》for PEP that:
"The statistical justification of this method is somewhat dubious"☺
So the principle of PEP is Not rigorous.

After Principle ，Computation comes:
For pruned-tree,Error counts: $n'(t)=15+0.5$
For un-pruned-tree,Error counts:
$n'(T_t)+SE(n'(Tt))$
$n'(T_t)=2(node 30)+0(node 31)+6(node 28)+2(node 29)+continuation\ Errors=10+4（node 30,node31,node28,node29）·0.5=12$
$pessmistic\ error \ counts=SE(n'(Tt))=\sqrt{\frac{12·（35-12）}{35}}=2.8$
then
$n'(T_t)+SE(n'(Tt))=12+2.8=14.8<15.5=n'(t)$
So,this tree should be kept and Not pruned

tools for print overline of texts:
https://fsymbols.com/generators/overline/

Pessimistic Error Pruning example of C4.5

猜你喜欢