Principal Components Analysis,PCA

主成分分析：对数据进行有损压缩。对于每个点 $x^{(i)} \in \mathbb{R}^{n}$ ，会有一个对应的编码向量 $c^{(i)} \in \mathbb{R}^{l}$ 。如果l比n小，就是压缩编码。

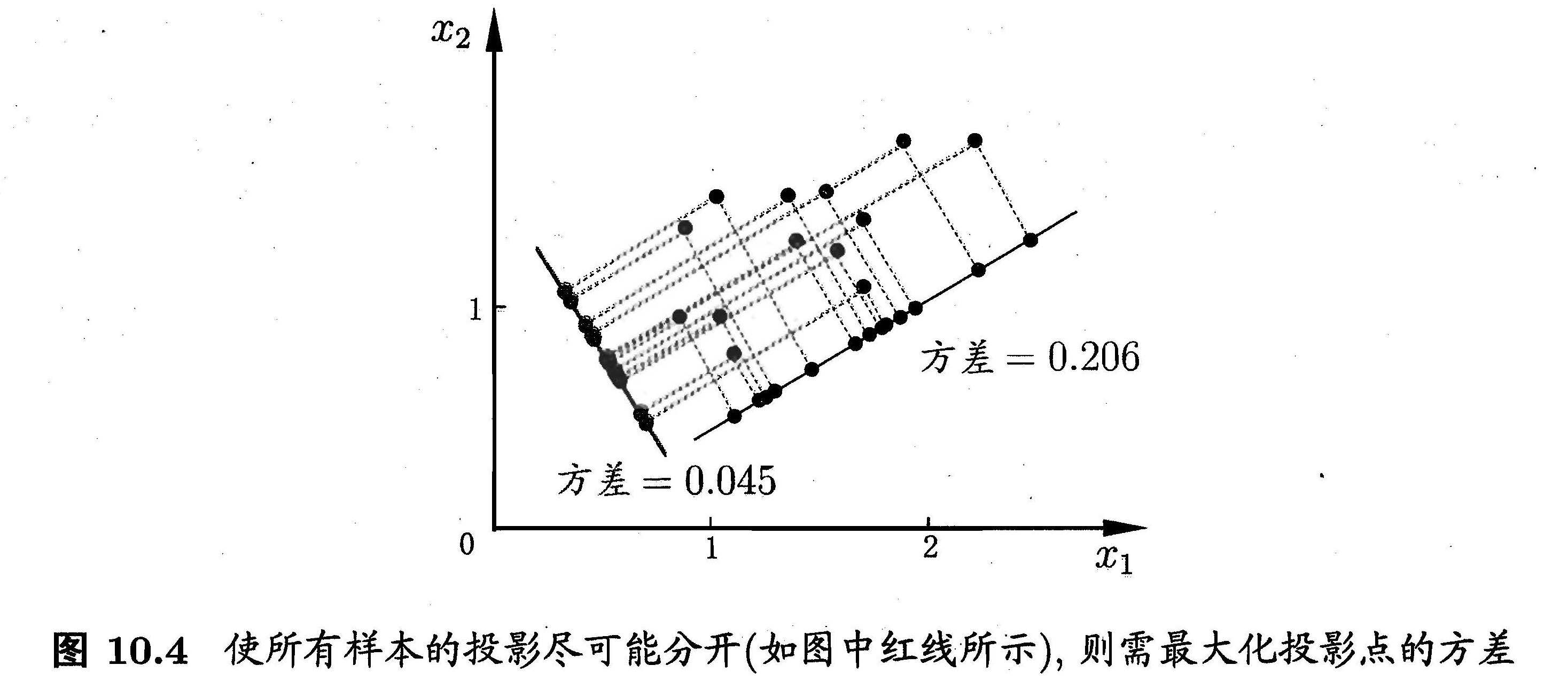
样本点 $x_{i}$ 在新空间中超平面上的投影为 $W^{T}x_{i}$ ，为了使所有样本点的投影尽可能分开，则应该使投影后的样本点方差最大。投影后的样本点方差为

$\sum_{i}W^{T}x_{i}x_{i}^{T}W$

于是优化目标写为

$\max_{W} tr(W^{T}XX^{T}W),\quad s.t.W^{T}W = I$

对上式进行拉格朗日乘子法可得

$XX^{T}W = \lambda W$

于是只需要对协方差矩阵 $XX^{T}$ 进行特征值分解，将求得的的特征值排序： $\lambda _{1}\geq \lambda _{2}\geq \geq ...\geq \lambda _{d}$ 。在取前 $d'$ 个特征值对应的特征向量构成 $W = (\omega _{1}, \omega _{2},...,\omega _{d'})$ ，这就是主成分分析的解。

输入：数据集 $D = \left \{ x_{1},x_{2},...,x_{m} \right \}$ ，

数据预处理：中心化 $x_{i} \leftarrow x_{i} - \frac{1}{m}\sum_{i=1}^{m}x_{i}$ 、均值归一化、特征缩放

目标：从n 维的数据降到 k 维。

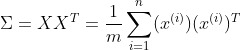
计算出协方差矩阵 $\Sigma =X X^{T}= \frac{1}{m}\sum_{i=1}^{n}(x^{(i)})(x^{(i)})^{T}$

计算矩阵的特征向量(奇异值分解)： [W,S,V] = svd(Sigma);

其中W就是特征向量矩阵，其列向量对应着投影方向。 $W = [w^{(1)}, w^{(2)},...,w^{(n)}] \quad W \in \mathbb{R}^{n\times n}$

我们选取前k项作为投影方向即可 $W_{reduce} = [w^{(1)}, w^{(2)},...,w^{(k)}] \quad W \in \mathbb{R}^{n\times k}$

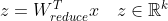
我们就得到数据集D的低维表达 $z = W_{reduce}^{T}x \quad z \in \mathbb{R}^{k}$

PCA仅需保留W与样本的均值向量。对应的最小的n-k个特征向量被舍弃，一方面，舍弃的这些信息后能使样本的采样密度增大；另一方面，当数据受到噪声影响时，最小的特征值所对应的特征向量往往与噪声有关，将它们舍弃能在一定程度起到去噪效果。

代码

去除平均值  
计算协方差矩阵  
计算协方差矩阵的特征值和特征向量  
将特征值从大到小排序  
保留最上面的N个特征向量  
将数据转换到上述N个特征向量构建的新空间中

def pca(dataMat, topK = 9999):
    meanVals = np.mean(dataMat,axis=0)

    meanRemoved = dataMat - meanVals
    covMat = np.cov(meanRemoved,rowvar=0)               #协方差cov
    eigVals,eigVects = np.linalg.eig(np.mat(covMat))    #计算矩阵特征向量
    eigValInd = np.argsort(eigVals)

    eigValInd = eigValInd[:-(topK +1):-1]
    redEigVects = eigVects[:,eigValInd]

    lowDDataMat = meanRemoved*redEigVects
    reconMat = (lowDDataMat*redEigVects.T)+meanVals
    return lowDDataMat, reconMat

Linear Discriminant Analysis,LDA

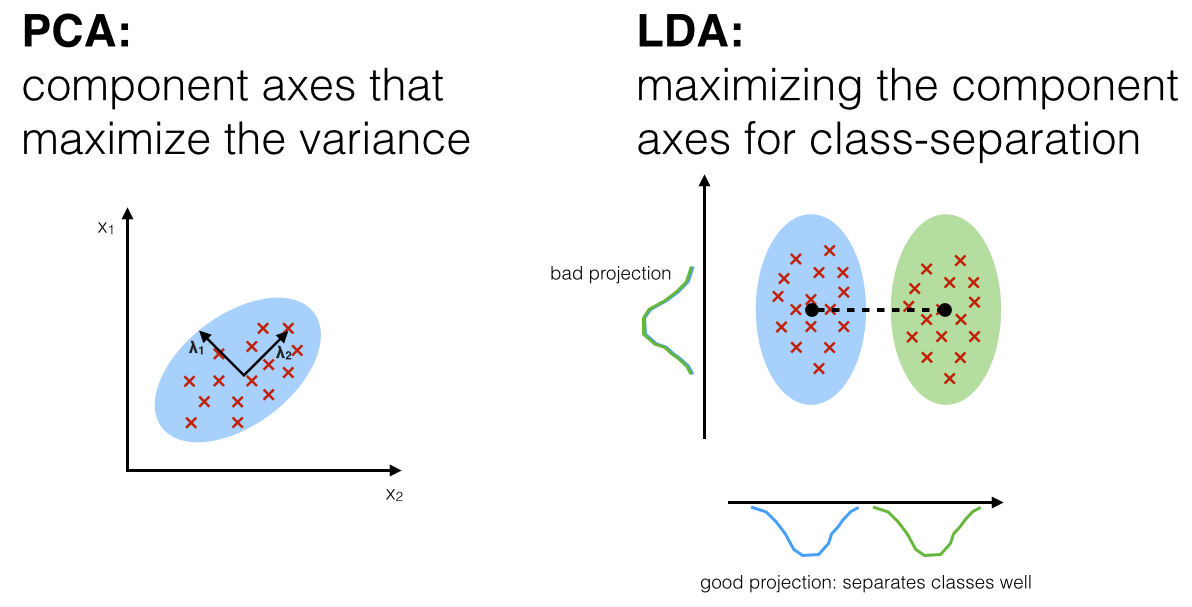
LDA是一种受监督的降维技术。目标是将数据集投影到具有良好类可分性的低维空间，以避免过度拟合（“维数灾难”）并且还降低计算成本。思路：给定训练数据集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能的近、异类样例的投影点尽可能远离；在对新样本分类时，将其投影到此直线上，再根据投影点的位置来确定类别。

给定二分类任务数据集，令 $X_{i}$ 、 $\mu_{i}$ 、 $\Sigma _{i}$ 分别代表第i类示例的集合、均值向量、协方差矩阵。若将数据投影到直线 $\omega$ 上，则两类样本的中心在直线上的投影为 $\omega^{T}\mu_{0}$ 和 $\omega^{T}\mu_{1}$ ；将所有样本点都投影到直线上，则两类样本的协方差分别为 $\omega^{T}\Sigma _{0}\omega$ 和 $\omega^{T}\Sigma _{1}\omega$ 。上述几个均为实数。

我们想让同类样例投影点的协方差尽可能小，即 $\omega^{T}\Sigma _{0}\omega+\omega^{T}\Sigma _{1}\omega$ 尽可能小；而使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大，即 $\left \| \omega^{T}\mu_{0}-\omega^{T}\mu_{1} \right \|_{2}^{2}$ 尽可能大。最大化目标

$J = \frac{\left \| \omega^{T}\mu_{0}-\omega^{T}\mu_{1} \right \|_{2}^{2}}{\omega^{T}\Sigma _{0}\omega+\omega^{T}\Sigma _{1}\omega}=\frac{\omega^{T}(\mu_{0}-\mu_{1})(\mu_{0}-\mu_{1})^{T}\omega}{\omega^{T}(\Sigma _{0}+\Sigma _{1})\omega}$

定义“类内散度矩阵: $S_{w} = \Sigma _{0}+\Sigma _{1}$ “类间散度矩阵” $S_{b}=(\mu_{0}-\mu_{1})(\mu_{0}-\mu_{1})^{T}$

$J = \frac{\omega^{T}S_{b}\omega}{\omega^{T}S_{w}\omega}$

这就是LDA的最大化目标。其中参数 $\omega$ 的求解公式为（证明略）

$\omega = S_{w}^{-1}(\mu_{0}-\mu_{1})$

当两类数据同先验、满足高斯分布且协方差相等时，LDA可达到最优分类。在多类分类中，假设N个类，第i类示例数位 $m_{i}$ 。其中 $\mu$ 是所有示例的均值向量。将类内散度矩阵 $S_{w}$ 重定义为每个类别的散度矩阵之和

$S_{w} = \sum_{i=1}^{N}S_{w,i}, S_{w,i}=\sum_{x \in X_{i}}(x-\mu_{i})(x-\mu_{i})^{T}$

$S_{b} =\sum_{i=1}^{N} m_{i}(\mu_{i}-\mu)(\mu_{i}-\mu)^{T}$

采用优化目标

$\max_{W} = \frac{tr(W^{T}S_{b}W)}{tr(W^{T}S_{w}W)}$

其中 $W\in \mathbb{R}^{d\times (N-1)}$ ， $tr(\cdot )$ 表示矩阵的迹:主对角线元素乘积。可通过如下广义特征值问题求解: $S_{b}W = \lambda S_{w}W$

W的闭式解是 $S_{w}^{-1}S_{b}$ 的N-1个最大广义特征值所对应的特征向量组成的矩阵。若将W视为投影矩阵，LDA将样本投影到N-1维空间，因此LDA也是经典的监督降维技术

算法流程

输入：数据集D,其中任意样本 $x_{i}$ 为n维向量， $y \in (C_{1},...,C_{k})$ 降维到的维度d。

输出：降维后的样本集 ${D}'$

计算类内散度矩阵 $S_{w}$

计算类间散度矩阵 $S_{b}$

计算矩阵 $S_{w}^{-1}S_{b}$

计算 $S_{w}^{-1}S_{b}$ 的最大的d个特征值和对应的d个特征向量 $\left ( \omega_{1},\omega_{2},...,\omega_{d} \right )$ ,得到投影矩阵W

对样本集中的每一个样本特征 $x_{i}$ ,转化为新的样本 $z_{i} = W^{T}x_{i}$

得到输出样本集

计算来自数据集的不同类的d维平均向量，其中d是特征空间的维度
计算类内 $S_{w}$ 和类间散射矩阵 $S_{b}$ .
计算散射矩阵的特征向量和相应的特征值.
选择对应于顶部k个本征值的k个本征向量，以形成维度d x k的变换矩阵
通过变换矩阵将d维特征空间X变换为k维特征空间X_lda


#  计算每个类别的均值向量
class_mean_vec = []
for i in df["class"].unique():
    # pd.mean()返回每一列的均值
    class_mean_vec.append(np.array(df[df["class"]==i].mean()[:4]))

# 计算Sw和Sb
Sw = np.zeros((4,4))
for i in range(2):
    per_class_sc_mat = np.zeros((4,4))                                      # 每个类别的协方差矩阵
    for j in df[df["class"]==i].index:
        row, mv = np.array(df.loc[j,:"entropy"]).reshape(4,1),class_mean_vec[i].reshape(4,1)
        per_class_sc_mat += np.dot((row-mv),((row-mv).T))
    Sw += per_class_sc_mat                                                  #每个类别协方差之和
print('within-class Scatter Matrix:\n', Sw)
feature_mean_vec = np.array(df.drop("class", axis=1).mean())
Sb = np.zeros((4,4))
for i in range(2):
    n = df[df["class"]==i].shape[0]
    mv = class_mean_vec[i].reshape(4,1)
    overall_mean = feature_mean_vec.reshape(4,1)
    Sb += np.dot(n*(mv-overall_mean),(mv-overall_mean).T)
print('between-class Scatter Matrix:\n', Sb)

# 求解Sw^{-1}Sb的广义特征值问题，以获得线性判别式。
e_vals, e_vecs = np.linalg.eig(np.linalg.inv(Sw).dot(Sb))

eig_pairs = [(np.abs(e_vals[i]), e_vecs[:,i]) for i in range(len(e_vals))]
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)



# 选择对应于top-k特征值的top-k特征向量
W = np.hstack((eig_pairs[0][1].reshape(4,1), eig_pairs[1][1].reshape(4,1)))

#W = np.stack((e_vecs[0],e_vecs[1]))
print('Matrix W:\n', W.real)

X = df[["var","skewness","curtosis","entropy"]]
X_lda = X.dot(W)

LDA总结

优点:

LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

缺点：

LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
LDA可能过度拟合数据。

LDA vs PCA

相同点：

两者均可以对数据进行降维
两者在降维时均使用了矩阵特征分解的思想
两者都假设数据符合高斯分布

不同点:

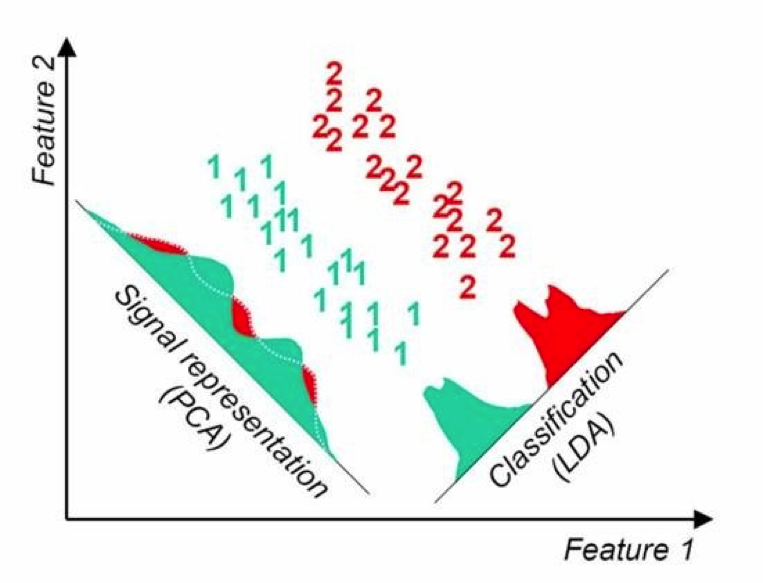
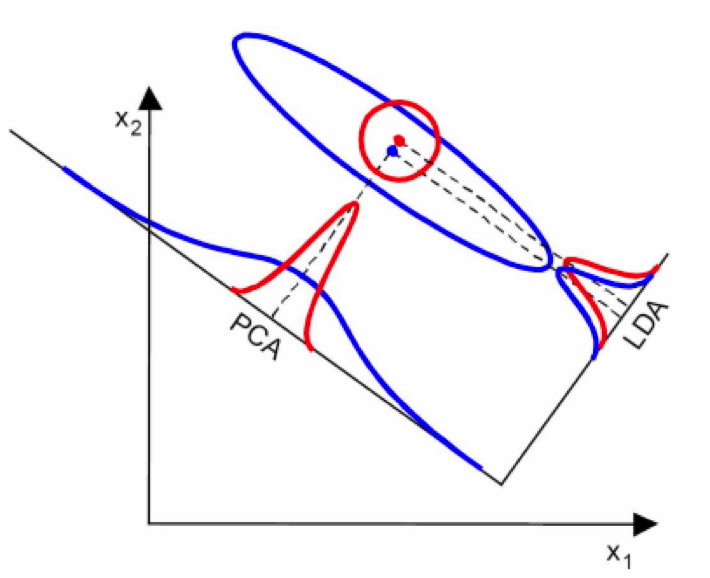
LDA是有监督的降维方法，而PCA是无监督的降维方法。在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识（PCA默认假设是：方差越大信息量越多，完全不在乎对于最后分类任务的影像。但是信息（方差）小的特征并不代表表对于分类没有意义，可能正是某些方差小的特征直接决定了分类结果，所以PCA会导致一些关键但方差小的分类信息被过滤掉. 所以LDA对PCA的附加优势是解决过度拟合问题）
LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。
LDA除了可以用于降维，还可以用于分类。
LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向
与PCA不同，LDA不需要标准化数据，因为它不会影响输出。标准化对LDA主要结果没有影响的原因是LDA分解了在协方差之间的比率，而不是具有其幅度的协方差本身（如PCA所做的那样）。

Feature

Principal Components Analysis,PCA

代码

Linear Discriminant Analysis,LDA

算法流程

LDA总结

LDA vs PCA

猜你喜欢