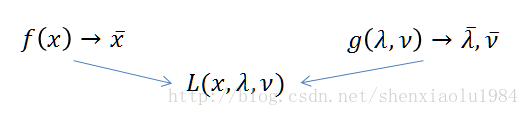【优化】对偶上升法(Dual Ascent)超简说明

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/shenxiaolu1984/article/details/78175382

本文从便于理解的角度介绍对偶上升法，略去大部分数学推导，目的是帮助大家看懂论文中的相关部分。

阅读本文前，请先参看这篇博客《共轭函数超简说明》。

对偶函数1

也称为拉格朗日对偶函数(Lagrange dual function)。

拉格朗日量

考虑定义域$D$上的最小化问题：

$$minimize\ f_0(x), x\in D$$

有$m$个不等式约束，以及$p$个等式约束：

$$f_i(x)\leq0, i=1,2...m$$

$$h_i(x)=0, i=1,2...p$$

这个最优化问题的拉格朗日量(Lagrangian)为：

$$L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^m\lambda_if_i(x) + \sum_{i=1}^p\nu_ih_i(x)$$

其物理意义参见这篇博客《拉格朗日乘子法超简说明》。

其中$\lambda, \nu$称为拉格朗日乘子(Lagrange multiplier)或者对偶变量(dual variable)，$x$称为原变量(primal variable)。

拉格朗日量是关于$x,\lambda, \nu$的函数。

拉格朗日对偶函数

对于定义域$D$上$x$的所有取值，拉格朗日量的最小值即为拉格朗日对偶函数(dual function)：

$$g(\lambda, \nu)=\inf_{x\in D}L(x,\lambda, \nu)$$

拉格朗日对偶函数是关于对偶变量$\lambda, \nu$的函数

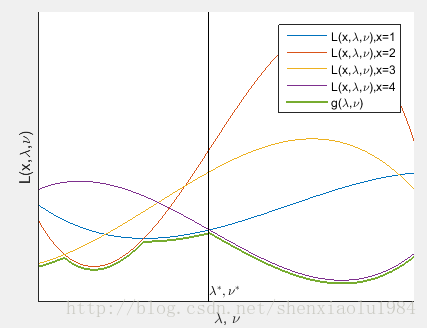
拉格朗日对偶函数可以看做是$x$取不同值时一族曲线的下界（绿线）。

当$\lambda\geq0$时，对于最优化问题的解$\bar x$，两个约束条件都非正：

$$\lambda_i f_i(\bar x)<=0, \ \nu_i h_i(\bar x)=0$$
于是，该解对应的曲线不超过原问题最优解：
$$L(\bar x,\lambda,\nu)\leq f_0(\bar x)$$
进一步，所有曲线的下界不超过原问题最优解：
$$g(\lambda, \nu)\leq f_0(\bar x)$$

换言之

$\lambda>0$时，拉格朗日对偶函数是最优化值的下界。

对偶函数与共轭函数

考虑线性约束下的最优化问题

$$minimize\ f_0(x), x\in D$$

$$Ax\leq b,Cx=d$$

其对偶函数：

$$g(\lambda, \nu)=\inf_x \left( f_0(x)+\lambda^T(Ax-b) + \nu^T(Cx-d)\right)$$

提取和$x$无关的项，凑出共轭函数形式：

$$g(\lambda, \nu)=-\lambda^Tb - \nu^Td + \inf_x \left( f_0(x)+\lambda^TAx + \nu^TCx\right)$$

$$=-\lambda^Tb - \nu^Td - \sup_x \left( (-A^T\lambda-C^T\nu)^Tx - f_0(x)\right)$$

$$=-\lambda^Tb - \nu^Td - f^*(-A^T\lambda-C^T\nu)$$

线性约束下的对偶函数可以用共轭函数表示。
其自变量为拉格朗日乘子的线性组合。

对偶问题2

上图绿线上的最高点，是对于最优化值下界的最好估计：

$$maximize\ g(\lambda,\nu)$$

$$subject\ to\ \lambda \geq0$$
这个问题称为原优化问题的拉格朗日对偶问题(dual problem)。

如果

• 强对偶条件成立3
• 对偶问题存在最优解$\bar \lambda,\bar \nu$

则：原问题$f_0(x)$的最优解$\bar x$也是$L(x,\bar \lambda,\bar \nu)$的最优解4

$L(x,\bar \lambda,\bar \nu)$是关于$x$的函数，相当于在图中$[\lambda,\nu] = [\bar \lambda,\bar \nu]$对应的竖线上，查找值最小曲线对应的$x$。

换言之：

原问题和对偶问题通过拉格朗日量联系了起来。

如果$f(x)$复杂，而$g(\lambda, \nu)$简单， 可以通过如下方式求解原问题：

• 求解 $\max g(\lambda, \nu)$得到$\bar \lambda, \bar \nu$
• 求解$\min L(x,\bar \lambda, \bar \nu)$得到$\bar x$

对偶上升法5

利用原问题和对偶问题的上述关系，有如下推论：

设第$k$次迭代得到原问题解$x^k$，对偶问题解$\lambda^k,\nu^k$

• 假设$\lambda^k,\nu^k$已经为对偶问题最优解
• 根据上述等价性，最小化$L(x,\lambda^k,\nu^k)$能得到原问题最优解$x^{k+1}$
  $$x^{k+1}=\arg \min_xL(x,\lambda^k,\nu^k)$$
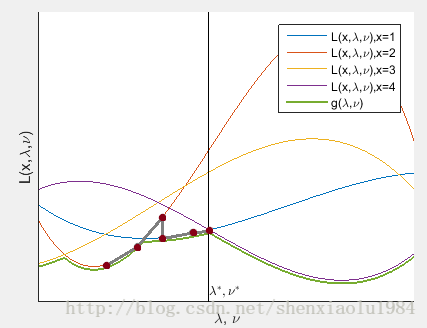
• $L(x,\lambda^k,\nu^k)$是$\lambda^k,\nu^k$位置上，不同$x$对应的$L$取值
• 所以，$x=x^{k+1}$的曲线处于所有曲线最下面。即$g(\lambda^k,\nu^k)=L(x^{k+1},\lambda^k,\nu^k)$
• 在该位置使用梯度上升法更新对偶问题解
  $$\lambda^{k+1}=\lambda^k + \alpha \cdot \frac{\partial L(x,\lambda,\nu)}{\partial \lambda} |_{x=x^{k+1},\lambda=\lambda^{k}, \nu=\nu^{k}}$$

$$\nu^{k+1}=\lambda^k + \alpha \cdot \frac{\partial L(x,\lambda,\nu)}{\partial \nu} |_{x=x^{k+1},\lambda=\lambda^{k}, \nu=\nu^{k}}$$

这一方法称为对偶上升法。下图的灰线示出解的变化：

---

1. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004. $\S$ 5.1 ↩
2. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004. $\S$ 5.2 ↩
3. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004. $\S$ 5.5.5 ↩
4. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004. $\S$ 5.5.5 ↩
5. S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2011. $\S$ 2.1 ↩