什么是拓扑排序?
拓扑排序顾名思义是一种排序算法,它用于给有向图排序。
有向图是由一组顶点和一组有方向的边组成的图,每条有方向的边都连接着有序的一对顶点,因此A -> B代表A可以到达B,并不代表B就能到达A。
拓扑排序的结果就是一个有向图的顶点序列(或称为拓扑序列)。
举例:计算机课程的安排
想要学习《C++程序设计》就需要先学习《计算机导论》
想要学习《数据结构和算法》就需要先学习《C++程序设计》
想要学习《网络操作系统》就需要先学习《计算机导论》
由此可以看出,这些活动都是有序的,每门课程就是图中的顶点,而有向边便是学习的顺序。你不能先学习《C++程序设计》,再学习《计算机导论》。就好比你不能先脱内衣,再脱外套一样。
那么,有向图是否就能拓扑排序呢?答案是不一定的。当图中存在环路时,比如学习A之前要学习B,学习B之前又要学习A,那么顺序就不可控了(到底A在前还是B在前?),故拓扑排序的充要条件是它是有向无环图。AOV网(顶点活动网)就是一种有向无环图。
同时,拓扑排序有时是不唯一的,如上图,学习顺序可以是:
《计算机导论》 -> 《C++程序设计》 -> 《网络操作系统》 ->《数据结构和算法》
也可以是:
《计算机导论》 -> 《网络操作系统》 ->《C++程序设计》 -> 《数据结构和算法》
由此可见,图中存在A->B的有向边,那么拓扑排序结果A必在B前面(从左指向右)。
拓扑排序两大步骤
1. 遍历顶点,找到入度为 0 的顶点(没有后继)
2. 删除该顶点及其相连的边,重复第一步,直到所有点都删除,由此构成的顺序就是拓扑序列
应用场景
拓扑排序不适用简单的计算环境,而在中大型的复杂环境中就显得重要了。
在Linux操作系统中,安装软件都是自动完成的,比如我安装A,需要依赖B和C,安装B需要依赖D、E和F,那么用拓扑排序就可以很好解决顺序问题:
D -> C -> E -> F -> B -> A
实现算法
基于入度的Kahn算法
伪代码
L <- 存放排序结果的集合
S <- 入度为0的顶点集合
while(S非空)
{
node n = S中的元素;
S.pop();
L.push(n);
for(n的邻接点m)
{
删除边n->m;
if(m的入度 == 0)
S.push(m);
}
}
if(图还有边)
return Error of 存在环路;
else
return L;
算法分析
1.计算所有顶点的入度
2.将入度为0的顶点加入集合
3.从图中删除该顶点及其相连的边,并将相邻顶点的入度-1
4.重复上述步骤
5.当集合为空检查是否还有边,有说明存在环路;否则排序结束
复杂度
遍历所有的顶点和边,因此时间复杂度为O(V+E)
基于DFS的算法
伪代码
L <- 存放排序结果的集合
S <- 出度为0的顶点集合
for(S中的所有顶点)
dfs(n)
void dfs(node n)
{
if(!vis[n]) //没有访问过
{
vis[n] = true;
for(所有满足m -> n的顶点m)
dfs(m);
}
L.push(n);
}
DFS是一种递归的方法,从出度为 0 的顶点开始,最先调用dfs却是最后加入集合中的,排在序列的最后面。
代码(C++实现)
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
#include <map>
using namespace std;
int V, E;
map< int, vector<int> > G;
bool visited[100]; // 已访问
queue<int> postorder; // 后序序列
void dfs(int v)
{
visited[v] = true;
for(vector<int>::iterator i = G[v].begin(); i != G[v].end(); i++)
{
int w = *i;
if(!visited[w]) dfs(w);
}
postorder.push(v);
}
void topological()
{
for (int v = 0; v < V; v++)
if (!visited[v])
dfs(v);
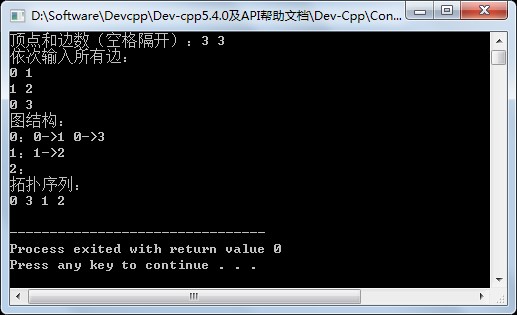
cout << "拓扑序列:" << endl;
stack<int> reverse;
while(!postorder.empty())
{
reverse.push(postorder.front());
postorder.pop();
}
while(!reverse.empty())
{
cout << reverse.top() << " ";
reverse.pop();
}
cout << endl;
}
void getData()
{
cout << "顶点和边数(空格隔开):";
cin >> V >> E;
cout << "依次输入所有边:" << endl;
for(int i = 0 ; i < E ;i++)
{
int v, w;
cin >> v >> w;
G[v].push_back(w);
}
}
void show()
{
cout << "图结构:" << endl;
for(int v = 0; v < V; v++)
{
cout << v << ":";
for(vector<int>::iterator i = G[v].begin(); i != G[v].end(); i++)
cout << v << "->" << *i << " ";
cout << endl;
}
}
int main(void)
{
getData();
show();
topological();
return 0;
}
复杂度
和Kahn算法一样,时间复杂度为O(V+E)