模块度Q——复杂网络社区划分评价标准

　　对复杂网络进行社区划分，需要有一些评价指标，来评判算法对网络划分结果的好坏优劣。如果我们预先知道网络的真实划分结果，那么我们可以用NMI（归一化互信息）去衡量算法划分结果和真实结果的重合程度，这个会在以后的文章中具体介绍。大多数情况下，我们是不知道网络的真实划分的，尤其是对于大型网络来说更是如此，复杂网络的命名明确的说明了这种现实情况。但是我们依然有方法可以量化或评判我们的社区划分水平，也就是今天要介绍的模块度（Modularity）概念，也称Q值。
　　从网上看到其他同学写的博客，首先对这方面介绍的不多，仅有的一些文章也是有好有坏，所以决定自己梳理一下，也是对其他人的分享。

资料

　　这次，先贴链接：
　　wiki：https://en.wikipedia.org/wiki/Modularity_(networks) 一定要搜英文的，中文版的并没有什么信息量。
　　原定义作者论文：Finding and evaluating community structure in networks (1)
　　　　　　　　　　Modularity and community structure in networks　(2)
　　一篇认为介绍的比较好的文章：Community Detection – Modularity的概念
　　建议是：看一下那篇博客，再看一下wiki，然后看一下原作者论文定义。
　　当然，也可以只看我的文章~O(∩_∩)O哈哈~。
　　之所以选择那篇博客是因为该作者从历史演进角度介绍了模块度概念的由来及变化，从方法论上来说，认识历史可以更好的认识现在，这几乎可以套用在对任何事物的认识上面。。。扯远了
　　

定义

　　我这里大概以通俗的语言翻译一下，严格的定义还是要看论文的，
　　定义一：
　　最早由Newman在文章(1)中给出的模块度的概念：
　　 Consider a particular division of a network into k communities. Let us define a k ×k symmetric matrix e whose element eij is the fraction of all edges in the network that link vertices in community i to vertices in community j.
　　 假设网络被划分为 $k$ 个社区，那么定义一个 $k \times k$ 的对称矩阵 $e$，它的元素 $e_{ij}$ 表示社区 $i$ 和社区 $j$ 之间的边的数量。
　　
　　The trace of this matrix $Tr e = \sum_{i}e_{ii}$ gives the fraction of edges in the network that connect vertices in the same community, and clearly a good division into communities should have a high value of this trace.
　　矩阵的迹$Tr e = \sum_{i}e_{ii}$，也就表示了在相同社区内节点之间的边集合。显然，社区划分的好，也就是社区内部节点之间联系密集，那么该值就越高，这与我们通常对社区的认识是一致的。
　　作者也指出，仅通过矩阵的迹这个值不能完全反应社区结构，因为如果把网络仅划分成1个社区的话，那么会导致$Tr e=1$。

　　So we further define the row (or column) sums $a_i = \sum_{j}e_{ij}$ , which represent the fraction of edges that connect to vertices in community $i$。
　　因此又定义了一个值 $a_i = \sum_{j}e_{ij}$，表示所有连接到社区$i$的边数量。
　　于是，作者定义了第一版模块度的概念：
　　

$$Q = \sum_{i}(e_{ii} - a_{i}^2) = Tr e - ||e^2||$$
　　 $||x||$ 表示矩阵 $x$ 的所有元素的和。
　　简单展开一下上面的公式会更清晰：
　　 $$Q = \sum_{i}(e_{ii} - a_{i}^2) = \sum_{i}e_{ii} - \sum_{i}a_{i}^2 = Tr e - ||e^2|| \qquad(1)$$

　　例如下面的网络，10个节点，12条边，被分成３个社区：
　
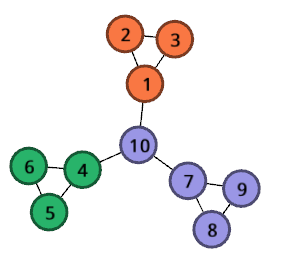
　　根据上述定义生成的社区矩阵为：
　　
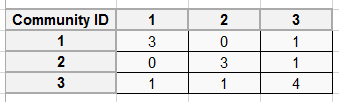
　　模块度$Q = \frac{3+3+4}{12} - (\frac{7}{2 \times 12})^2 - (\frac{7}{2 \times 12})^2 - (\frac{10}{2 \times 12})^2 = 0.49$

　　定义二：
　　再来看第二版定义：
　　Newman在论文(2)中更新了模块度Q的定义，增加了矩阵的表达，感觉更不直观了。
　　个人感觉从wiki里的定义理解更清楚一些，下面是一些定义及推导：
　　Modularity is the fraction of the edges that fall within the given groups minus the expected such fraction if edges were distributed at random.
　　模块度 = （落在同一组内的边的比例） 减 （对这些边进行随机分配所得到的概率期望）
　　为了说明上述公式，对定义如下内容：
　　假设网络有$n$个节点，有$m$条边，节点$v$的度表示为$k_v$。
　　将网络的邻接矩阵表示为$A$，$A_{vw}=0$ 表示节点$v$和$w$之间没有边，$A_{vw}=1$ 表示有边。
　　定义变量$s$，$s_{vw}=1$表示$v$和$w$属于同一社区，$s_{vw}=-1$表示不在同一社区，那么可以用$δ_{vw}=\frac{1}{2}(s_{vw}+1)$量化表示$v$和$w$是否在同一社区，如果是则等于1，不是则等于0.
　　那么上述模块度定义就可以表示为：
　　

$$Q=\frac{1}{2}\frac{\sum_{vw}A_{vw}}{m}δ_{vw} - （对这些边进行随机分配所得到的概率期望）$$
　　 $\sum_{vw}A_{vw}δ_{vw}/m$ 表示在同一社区内的边的数量占所有边数量的比例， 乘以 $1/2$，是因为对每条边计算过两次。
　　
　　以上这部分计算很清楚，下面主要看那个期望值如何计算。
　　这里面用到了Configuration Models，大体意思就是，对网络的边进行随机分配，需要将每条边切断一分为二，切断的点我们称作末梢点(stub)，这样 $m$条边就会产生 $l_{n}=2m=\sum_{v=1}^nk_{v}$个末梢点，随机的将这 $l_n$个末梢点进行连接，包括同一节点拥有的末梢点的自连接。这样可以保持每个节点原有的度不变的条件下，可以得到一个完全随机网络。
　　在该随机网络下，任意两点 $v、w$连接边数的期望值是： $exp_{vw}=\frac{k_{v}k_{w}}{l_{n}}=\frac{k_{v}k_{w}}{2m}$
　　因此，节点 $v$和 $w$的实际边数与随机网络下边数期望之差为： $A_{vw}-\frac{k_vk_w}{2m}$
　　模块度最终可表示为： $$Q=\frac{1}{2m}\sum_{vw}(A_{vw} - \frac{k_{v}k_{w}}{2m}) δ_{vw} \qquad (2)$$
　　定义 $e_{ij}$表示连接社区 $i$ 和 $j$ 的边的总数， $e_{ij}=\sum_{vw}\frac{A_{vw}}{2m}δ_{vi}δ_{wj}$， $a_i$表示连接 社区 $i$的边的总数， $a_i=\sum_je_{ij}=\frac{k_i}{2m}$，那么模块度可以表示为： $$Q=\frac{1}{2m}\sum_{vw}A_{vw}δ_{vw}-\frac{1}{2m}\sum_{vw}\frac{k_{v}k_{w}}{2m}δ_{vw}=\sum_{i=1}^c(e_{ii}-a_{i}^2)$$
　　
　　可以看到，虽然初始含义不同，但经过推导，模块度的公式(1)和公式(2)具有一致的表现形式，而且最终的结果非常简单。
　　应当注意，模块度的取值范围为： $[-1/2, 1)$，有可能得到负值。
　　

代码实现

　　虽然推导过程非常复杂，但是最终形式非常简单，代码自然也清晰易懂。

#python2.7
#type(graph) = networkx.Graph
def Q(graph, cluster):
    e = 0.0
    a_2 = 0.0
    cluster_degree_table = {}
    for vtx, adj in graph.edge.iteritems():
        label = cluster[vtx]
        for neighbor in adj.keys():
            if label == cluster[neighbor]:
                e += 1
        if label not in cluster_degree_table:
            cluster_degree_table[label] =0
        cluster_degree_table[label] += len(adj)
    e /= 2 * graph.number_of_edges()

    for label, cnt in cluster_degree_table.iteritems():
        a = 0.5 * cnt / graph.number_of_edges()
        a_2 += a * a

    Q = e - a_2
    return Q