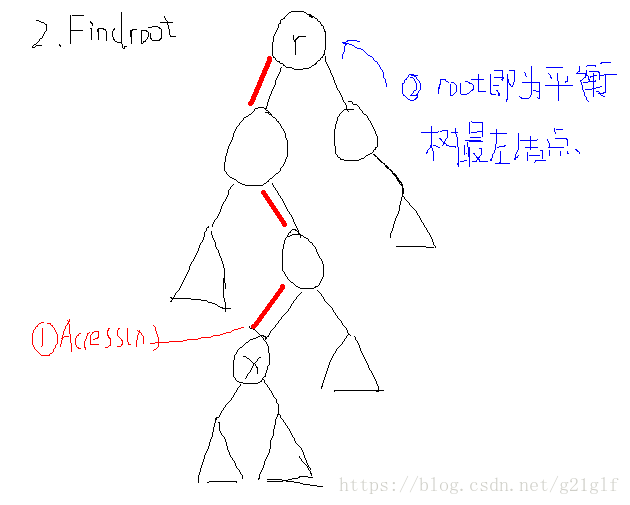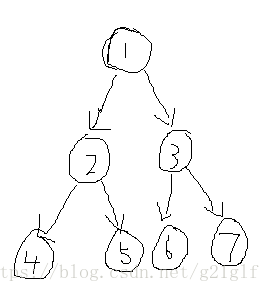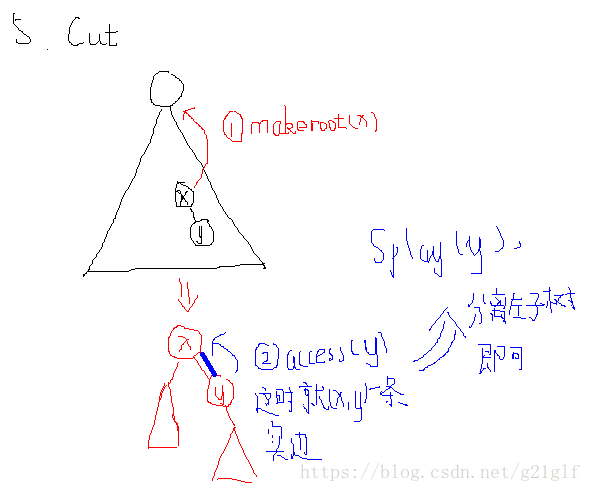什么是动态树?
动态树(Dynamic Tree)问题是指在树上动态维护相关信息的问题。
一般的动态树问题中,会要求我们维护一个由若干棵子结点无序的有根树组成的森林。并且要求这个数据结构支持对树的分割(删边),合并(加边),对某个点到它的根的路径的某些操作(路径操作)。有时,动态树问题还会涉及对某个点的子树进行的某些操作(子树操作),而涉及子树操作问题的动态树问题更加复杂,需要用到更加复杂的数据结构。然而蒟蒻并不会做这种高级的题目,所以就讲讲简单的几种操作。
关于LCT的一些笔记
LCT(Link-Cut Trees)是解决这类动态树问题的一种数据结构。这个数据结构可以在均摊O(log n)的时间内实现上述动态树问题。
LCT 的详细介绍,大家可以参考杨哲的《QTREE 解法的一些研究》,这里贴文库链接:https://wenku.baidu.com/view/75906f160b4e767f5acfcedb.html
简单来说,LCT 与树链剖分一样,会对节点的儿子进行划分。树链剖分中根据节点子树大小来划分轻重儿子,并用数据结构维护重链;而 LCT 则会将儿子划分为虚、实两种儿子,相应的边称为虚边或实边,且任意时刻一个节点最多只会有一个实儿子(可能没有)。由于树的形态会改变,因此 LCT 不是严格的划分虚实儿子,而是动态地改变,它同样使用了数据结构来维护实链(连续的实边),并且用的是更加灵活的 Splay.
关于LCT的一些基本定义:
1.深度:深度越大(小),到根节点路径的距离越长(短)。
2.实边:一个非叶节点,向它的儿子中的一个连一条特殊的边,称为实边;该非叶节点向它的其他儿子所引的边均为虚边。注意,对于某些非叶节点,它与它儿子们所连的边可能全部是虚边。
3.实路径(链):由若干条实边首尾相连而成的、不可伸长的路径称为实路径。由实边的定义可知,实路径上的点深度各不相同且为连续自然数。其中,不可伸长指的是,设一个实路径上最浅节点为 u,则 u 和 u 的父节点之间的边不能是实边;设一个实路径最深节点为 v,则 v和它儿子们所连的边全是虚边。
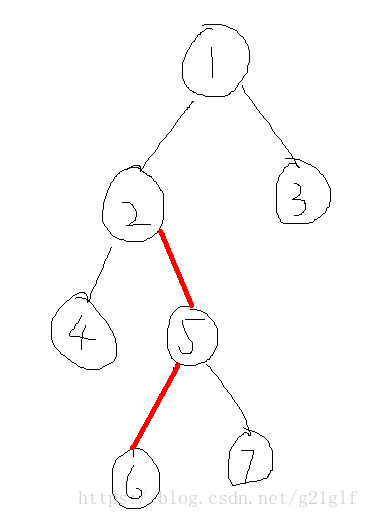
4.实路径的父亲:可以得出各条实路径之间是由虚边连接,对于一条实路径,我们定义它的实路径父亲(Path_Parent)为它的最浅的节点的父亲,如下图:
其中红色路径为实路径,那么对于2-5-6这条实路径,它的实路径的父亲就为2的父亲,即为1。
关于与LCT的一些基本操作
用 Splay维护实路径:由于每条实路径是由首尾相连的实边构成的,因此实路径上任意两个点都是祖先与子孙的关系。换句话说,如果用深度作为关键字给结点排序,那么我们将得到一个唯一的有序结点序列。
基于这个思想,我们将这个结点序列用平衡树维护,平衡树中每个结点的左子树中结点在实路径中的深度都小于该结点,右子树中的都大于该结点,因此平衡树的最左结点对应该路径的头部,最右结点对应该路径的尾部。
一些基本操作(注意:在操作过程中并不需要考虑Splay的形态,而是只用考虑当前树的形态):
1.Access(x):以x为起点一直到根节点构造出一条链。
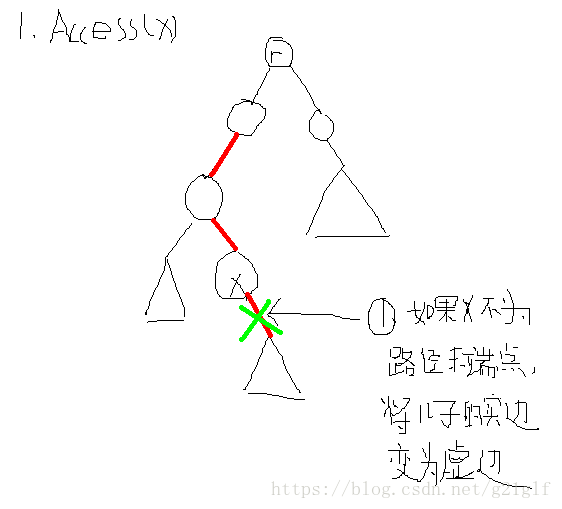
这是针对某个结点 x 的操作, 该操作将 x 到根结点的路径上的所有边都变为实边, 当然,为了保持实边、虚边划分的性质,一部分原来的实边也要相应变为虚边。注意该操作会将 x下方的实边变为虚边。该操作的步骤如下:
(1):如果结点 x 不是其所在实路径的尾部, 即 x有子结点与之用实边相连, 那么需要 “断开”这条边(断开并不是将这条边删除,而只是将其转变为虚边)。方法是首先将结点 x用 Splay操作旋转到所在平衡树的根结点,然后 x 肯定有右子树,故将 x 与 x的右子树分离,同时将 x 的右子树的 Path_Parent 设置为 x。
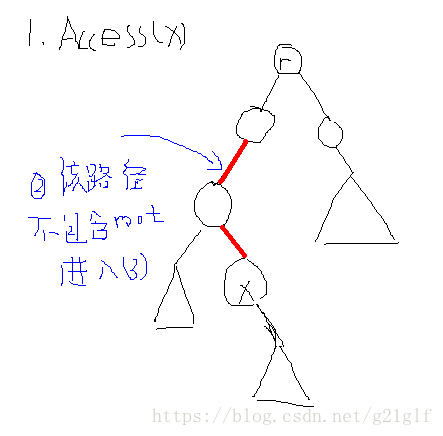
(2):如果结点 x所在的平衡树包含根结点,那么该过程结束;否则,转步骤(3);
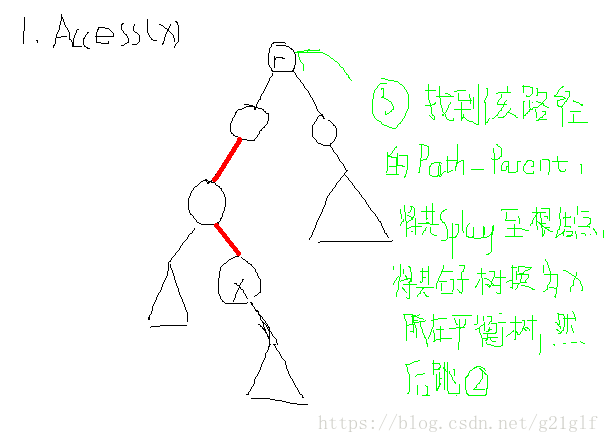
(3):设 y 为 x 所在平衡树的 Path_Parent。将 y 用 Splay 操作旋转到其所属平衡树的根结点,并且用 x 所在的平衡树替换 y的右子树,这样就实现了实路径的向上延伸。当然到这里还没有结束,我们需要分离原来 y 的右子树,y原来的右孩子记为 P。此时 P 的 Path_Parent就为 y了,然后继续转步骤(2)。
实际实现时, 我们并不需要显示维护出 Path_Parent, 我们可以稍微更改 Splay中的实现,即我们考虑 Splay中根节点的 fa,我们并不需要将其置为 0,而是将其置为 Path_Parent,这样每个点的父亲,要么是实路径上的点,要么是它所处实路径的 Path_Parent,特别地,这棵树的根节点的 Path_Parent 为 0。这样的话一个点,它的 fa的左右儿子可能都不为它,因此判断根节点的条件也需要稍微修改一下。下面给出具体实现过程的图示(红边表示实边,帕金森晚期患者):
因为维护的关键字为深度,所以删除前Splay上肯定有x的子树那一段,所以将x通过Splay旋转到根节点处,直接将x的右子树与它分离,并把右子树的Path_Parent改为x(实际操作并不需要)
需要注意的是,将y的右子树换成x所在平衡树后,原右子树的Path_Parent就变成了y。
2.Findroot(x):找到节点x所在树的根节点。
有了 Access(x)操作,寻找树根的操作就So easy了。我们只要对结点 x 执行Access(x),便使得 x 与要找的根结点在同一棵平衡树中了。然后,要找的根结点一定是实路径的头部(因为深度最小),即平衡树中的最左结点。
图示:
3.Makeroot(x):使节点x成为所在树的根节点。
首先我们观察下面这个图:
对于一棵有根树而言,它的父子关系是确定了的,图中由父亲指向儿子。
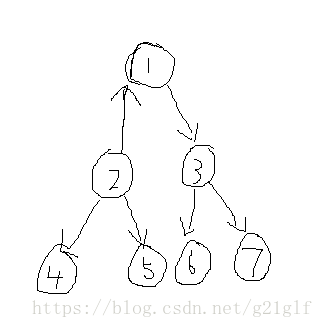
那么如果我们把2作为整棵树的根呢?那么它就会长这样:
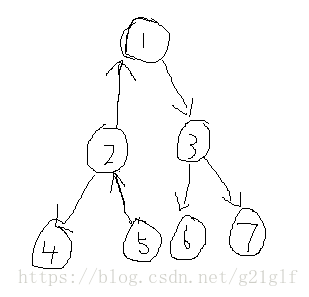
如果还没发现规律的话,我们再以5为整棵树的根:
没错,以谁为根,就是将该点到根节点路径父子关系取反,所以该操作等价于将从结点 x到当前根结点的路径上的所有树边的方向取反。首先执行 Access(x),我们便已经将该路径取出了。由于路径是用平衡树维护,所以需要执行的是平衡树的区间翻转操作,我们可以借鉴线段树的打标记(懒操作)思想,给平衡树结点也用打标记的方式来完成反序操作。这里由于是对整棵平衡树反序,所以标记应该打在平衡树的根结点处。打标记后注意在其他操作的地方(例如旋转后)及时下传以及更新。
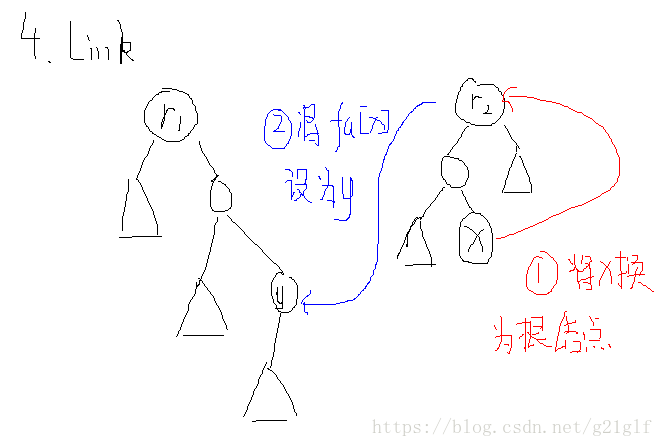
4.Link(x,y):使x成为y的子节点,也就是连一条(x,y)的边
这只需要执行一次 MakeRoot(x)操作,随后将x的fa置为y即可。
图示:
5.Cut(x,y):删除树中(x,y)这条边
该操作执行时,首先将 x 置为有根树的根结点,从而保证 y一定是 x 的子结点。再对 y执行 Access 操作,我们便将 x 和 y 合并到同一平衡树中了。此时对 y 执行 Splay 操作使其成为所在平衡树的根结点,同时分离 y和 y 的左子树,便完成了边的删除操作。(此时若树中存在(x,y)这条边,则 y的左子树一定只有 x 这一个节点)。
图示:
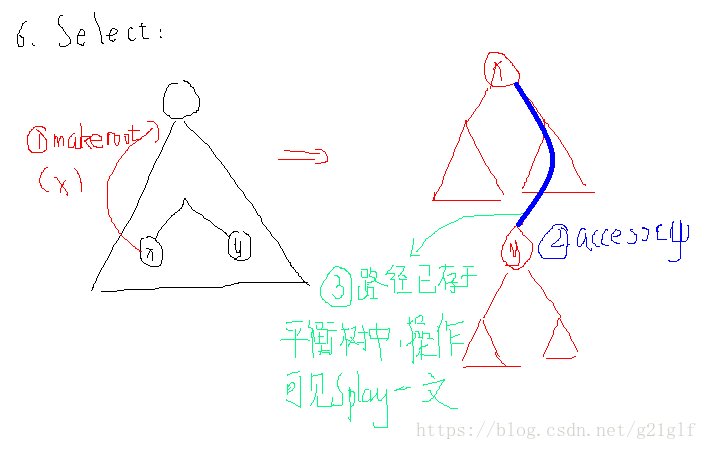
6.Select(x,y):取出(x,y)在树中的路径从而进行区间操作。
执行一次 MakeRoot(x)将 x 置为其所在树的根,再执行一次 Access(y)操作,就将 x 与 y以及它们路径上的所有点整合至同一棵平衡树中了。 此时我们在平衡树的根节点上打上标记或者直接查询信息即可。
图示: