机器学习算法——岭回归

转载自：http://blog.csdn.net/google19890102/article/details/27228279

一、一般线性回归遇到的问题

    在处理复杂的数据的回归问题时，普通的线性回归会遇到一些问题，主要表现在：

• 预测精度：这里要处理好这样一对为题，即样本的数量和特征的数量
  • 时，最小二乘回归会有较小的方差
    
  • 时，容易产生过拟合
    
  • 时，最小二乘回归得不到有意义的结果
    
• 模型的解释能力：如果模型中的特征之间有相互关系，这样会增加模型的复杂程度，并且对整个模型的解释能力并没有提高，这时，我们就要进行特征选择。

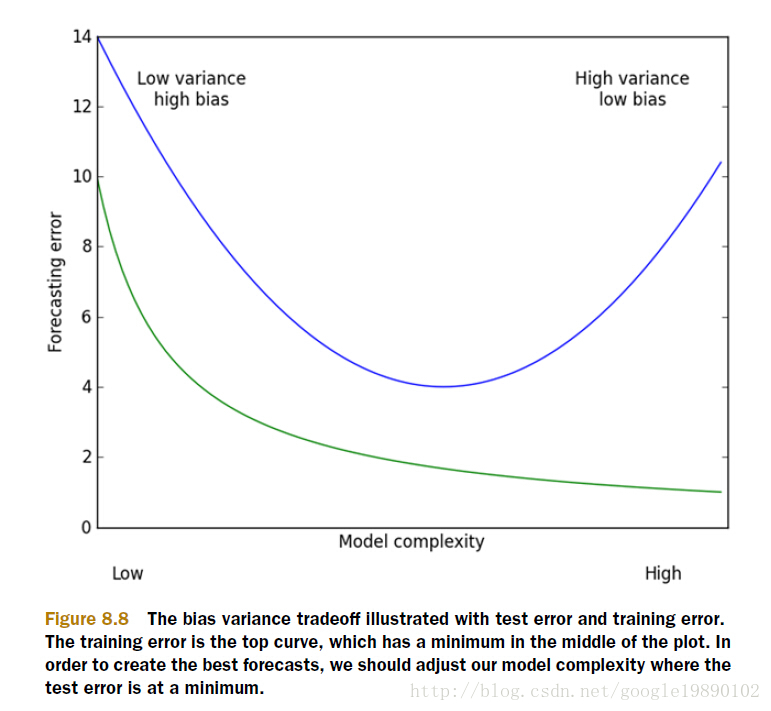
以上的这些问题，主要就是表现在模型的方差和偏差问题上，这样的关系可以通过下图说明：

（摘自：机器学习实战）

方差指的是模型之间的差异，而偏差指的是模型预测值和数据之间的差异。我们需要找到方差和偏差的折中。

二、岭回归的概念

    在进行特征选择时，一般有三种方式：

• 子集选择
• 收缩方式(Shrinkage method)，又称为正则化(Regularization)。主要包括岭回归个lasso回归。
• 维数缩减

    岭回归(Ridge Regression)是在平方误差的基础上增加正则项

,

通过确定的值可以使得在方差和偏差之间达到平衡：随着的增大，模型方差减小而偏差增大。

    对求导，结果为

令其为0，可求得的值：

三、实验的过程

    我们去探讨一下取不同的对整个模型的影响。

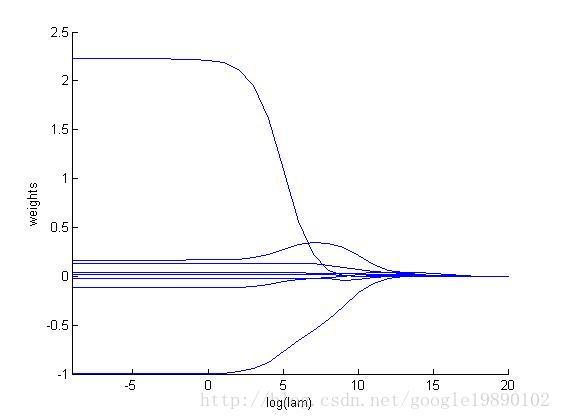
那么这个图什么意思呢？

(横轴是循环次数就是相关岭系数 纵轴是回归系数) 从图像中可以看出，在这八个系数中有两个距离0比较远，所以数据的主要预测就可以依靠这两个系数

MATLAB代码

主函数

[plain]  view plain  copy

1. %% 岭回归(Ridge Regression)  
2.   
3. %导入数据  
4. data = load('abalone.txt');  
5. [m,n] = size(data);  
6.   
7. dataX = data(:,1:8);%特征  
8. dataY = data(:,9);%标签  
9.   
10. %标准化  
11. yMeans = mean(dataY);  
12. for i = 1:m  
13.     yMat(i,:) = dataY(i,:)-yMeans;  
14. end  
15.   
16. xMeans = mean(dataX);  
17. xVars = var(dataX);  
18. for i = 1:m  
19.     xMat(i,:) = (dataX(i,:) - xMeans)./xVars;  
20. end  
21.   
22. % 运算30次  
23. testNum = 30;  
24. weights = zeros(testNum, n-1);  
25. for i = 1:testNum  
26.     w = ridgeRegression(xMat, yMat, exp(i-10));  
27.     weights(i,:) = w';  
28. end  
29.   
30. % 画出随着参数lam  
31. hold on  
32. axis([-9 20 -1.0 2.5]);  
33. xlabel log(lam);  
34. ylabel weights;  
35. for i = 1:n-1  
36.     x = -9:20;  
37.     y(1,:) = weights(:,i)';  
38.     plot(x,y);  
39. end  

代码的数据集可以网上搜，github上就有。

岭回归求回归系数的函数

function [ w ] = ridgeRegression( x, y, lam )  
    xTx = x'*x;  
    [m,n] = size(xTx);  
    temp = xTx + eye(m,n)*lam;  
    if det(temp) == 0  
        disp('This matrix is singular, cannot do inverse');  
    end  
    w = temp^(-1)*x'*y;  
end

补充一些总结：

4. 正则化

对较复杂的数据建模的时候，普通线性回归会有一些问题：

（1） 稳定性与可靠性 : 当X列满秩的时候，使用线性回归有解析解，

如果n和m比较接近，则容易产生过拟合；如果n  是奇异的，最小二乘回归得不到有意义的结果。因此线性回归缺少稳定性与可靠性。

（2）模型解释能力的问题 包括在一个多元线性回归模型里的很多变量可能是和响应变量无关的；也有可能产生多重共线性的现象：即多个预测变量之间明显相关。这些情况都会增加模型的复杂程度，削弱模型的解释能力。这时候需要进行变量选择（特征选择）。

4.1 Ridge Regression （岭回归或脊回归）

代价函数

即在线性回归的代价函数后面加上一个惩罚项，对拟合函数进行平滑，防止过拟合。同样求导可得

岭回归通过引入2范数的惩罚项，损失了拟合的无偏性，但是此时在任何条件下都有解析解，换取了稳定性。

概率解释

上面对线性回归进行概率解释的时候，通过求解最大似然估计，得到普通线性回归的代价函数，如果不采用最大似然估计方式，如通过最大后验概率估计，引入合适的先验函数就可以得到岭回归的概率解释。

记训练集合，则后验概率

通过最大后验概率求参数，即

假设,则类似线性回归的推到可得到岭回归的代价函数。

4.2 Lasso

代价函数

与岭回归不同的是，Lasso采用的惩罚项是1范数，因为1范数不可导，因此没有解析解，采用迭代求解，其求解方法有很多，如最小角回归，其形式和sparse coding中的编码过程一致，因此sparse coding常用的方法如 

feature-sign search算法。

Lasso得到的结果是稀疏的，因此相比于岭回归，Lasso还有特征选择的作用，从下图可以看出

概率解释

与岭回归相同，采用极大后验概率估计的方法，只是此时的先验概率为：

即参数是独立的，且先验为拉普拉斯概率。

4.3 Elastic net 

代价函数

Elastic net 将岭回归和Lasso的代价函数组合到一起。

5 三种正则化方式对比

Ridge Regression：

• 岭回归能防止线性回归的过拟合，相对于普通的线性回归虽然估计的精度降低，但是通过损失无偏性，换取了稳定性，模型的泛化能力增强。

Lasso：

• 岭回归得到的系数是稠密的，即系数都为非零值，因此做预测时，所有的特征都会用到，模型的可解释性不强
• Lasso得到的系数是稀疏的，因此相对于岭回归，Lasso还有特征选择的作用

Elastic net：

• 当n>m时，即特征的数目远大于样本的数目时，Lasso最多选择n个特征，即特征选择的数量受样本数量的限制
• 在一组相似的特征中，Lasso只会选择其中一个，但是有时特征虽然相关但是对于模型都很重要，此时应采用Elastic net
• Elastic net通过l1范数产生稀疏，l2范数来消除特征选择数量的限制，鼓励相似的特征组具有同样的稀疏性，类似于group sparse coding

[plain]  view plain  copy

1. function [ w ] = ridgeRegression( x, y, lam )  
2.     xTx = x'*x;  
3.     [m,n] = size(xTx);  
4.     temp = xTx + eye(m,n)*lam;  
5.     if det(temp) == 0  
6.         disp('This matrix is singular, cannot do inverse');  
7.     end  
8.     w = temp^(-1)*x'*y;  
9. end