Bayes估计

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/wzgbm/article/details/51734266

1) 统计推断的基础

　　在统计推断中有三种信息:先验信息,样本信息,总体信息.
　　1) 总体信息：总体信息即总体分布或总体所属分布族提供的信息．总体信息是很重要的信息，只要有总体信息，就要想方设法在统计推断中使用,为了获取此种信息往往耗资巨大．

　　2) 样本信息：样本信息即抽取样本所得观测值提供的信息．没有样本就没有统计学可言．
　　
　　3) 先验信息：先验信息即是抽样（试验）之前有关统计问题的一些信息.一般说来，先验信息来源于经验和历史资料（比如我们总能识别自己亲朋好友的声音，从而给出不同的声音对应的人，这样对判断的概率还是很有影响的）．先验信息在日常生活和工作中是很重要的．

---

2) Bayes统计的三个基本假设

　　假设1：任一未知量θ都可看作随机变量，可用一个概率分布去描述，这个分布称为先验分布；即样本分布中的参数不是常数,而是随机变量.这个随机变量的分布可从先验信息中归纳出来，这个分布称为先验分布，其密度函数用$\pi(\theta)$表示。
　　假设2： 任一未知量θ先验分布是已知的；
　　假设3： 样本分布是样本在给定θ时的条件分布.

---

3) 贝叶斯公式

　　1) 离散型

$$P({B_i}|A) = \frac{{P({B_i}A)}}{{P(A)}} = \frac{{P(A|{B_i})P({B_i})}}{{\sum\limits_{j = 1}^n {P(A|{B_j})P({B_j})} }}$$
　　2) 连续型
　　在获得样本 $x$后, $\theta$的后验分布就是在给定 $X=x$的条件下 $\theta$的条件分布,记为 $\pi(\theta|x)$.对于有密度的情形,它的密度函数为: $$\pi (\theta |x) = \frac{{\pi (x,\theta )}}{{\pi (x)}} = \frac{{p(x|\theta )\pi (\theta )}}{{\int_\theta {p(x|\theta )\pi (\theta )d\theta } }}$$
其中, $\pi (x,\theta ) = p(x|\theta )\pi (\theta )$为X和θ的联合分布,而 $\pi (x) = \int_\theta {p(x|\theta )\pi (\theta )d\theta }$为X的边缘分布.

---

4) 贝叶斯学派的基本观点

$先验信息 \oplus 抽样信息 \Rightarrow 后验信息$

　　贝叶斯学派的基本观点是：后验分布中集中了先验分布和样本两部分信息.因此所有关于参数θ的推断(估计)都应该从后验分布出发．应理解为贝叶斯公式.

---

５) 分步族

分布族可以理解为具有相同形式的分布函数.比如不同参数的正态分布,都是正态分布族.

---

6) 先验分布的选取

　　先验分布有不同的类型,比较重要的两个概念是无信息先验和共轭先验分布.

a. 同等无知

　　在没有先验信息的情况下，对未知的参数$\theta$的所有可能取值同等对待。

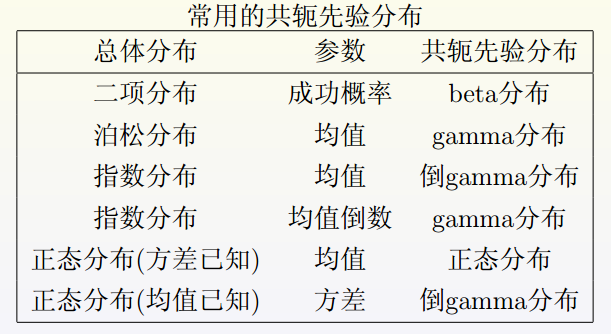
b.共轭先验分布

定义：设$\Psi$表示由$\theta$的先验分布$\pi(\theta)$构成的分布族.如果对任取的$\pi\in\Psi$及其样本值$x$,后验分布$\pi(\theta|x)$仍属于$\Psi$,那么称Ψ是一个共轭先验分布族(conjugate prior distribution family).而此时先验分布$\pi(\theta)$称为θ的共轭先验分布.

具体参考（http://www.duzelong.com/wordpress/201506/archives541/）

---

7) 贝叶斯估计

　　如何从后验分布出发来构造参数估计?有两种不同的,但往往是殊途同归的思路可循.

a. 直观统计法

由后验分布$\pi(\theta|x)$估计$\theta$有三种常见的方法：
　　使用后验分布的众数作为$\theta$的点估计的众数后验估计；
　　使用后验分布的中位数作为$\theta$的点估计的后验中位数估计；
　　使用后验分布的期望作为$\theta$的点估计的后验期望估计。
使用最多的后验期望估计，它也被简称为贝叶斯估计。

b. 度量法

　　第二种思路就是提出适当的准则,用一定的量来度量估计的优劣,并在可能的场合下寻找最优估计.

　这里介绍在”统计决策理论”的框架内用于度量估计优劣的两个概念:损失函数与风险.
　　决策就是对一件事要作决定.它与推断的差别在于是否涉及后果.统计学家在作推断时是按统计理论进行的,很少考虑结论在使用后的损失.可决策者在使用推断结果时必需与得失联系在一起,能带来利润的就会用,使他遭受损失的就不会被采用,度量得失的尺度就是损失函数.它是著名的统计学家A.Wald(1902-1950)在40年代引入的一个概念.从实际归纳出损失函数是决策的关键.
　　贝叶斯决策:把损失函数加入贝叶斯推断就形成贝叶斯决策论,损失函数被称为贝叶斯统计中的第四种信息.

　　当损失函数$L(\theta,a)$和$\theta$的一个估计$\hat{\theta}$都给出来后，损失$L(\theta,\hat{\theta})$是随机变量。评估一个估计量$\hat{\theta}$的好坏，不能仅根据它在一时一地的表现，而应该根据它在$\theta$取任何可能的值，及样本取任何可能的值时的平均表现来判断，我们定义$\hat{\theta}$的“风险”为：

$$R_{\theta} = E(L(\theta,\hat{\theta}))$$
　　E的含义是对 $\theta$和 $\hat{\theta}$的联合概率的数学期望，风险的概念就是平均损失，平均计算是即针对与样本又针对于参数计算的，风险越小则估计越好。
　　我们再定义一个估计量的后验风险： $$r_{\hat\theta(X)} = E(L(\theta,\hat{\theta})|X)$$
　　后验风险 $r_{\hat\theta}(X)$是在给定样本 $X$的时， $\hat{\theta}$的条件平均损失。由数学期望的性质有： $$R_{\hat\theta} = E(r_{\hat\theta}(X))$$
　　因此，求风险 $R_{\hat\theta}$分为两步。第一步，固定样本，求出损失函数对 $\theta$的条件期望；第二步，求出风险。