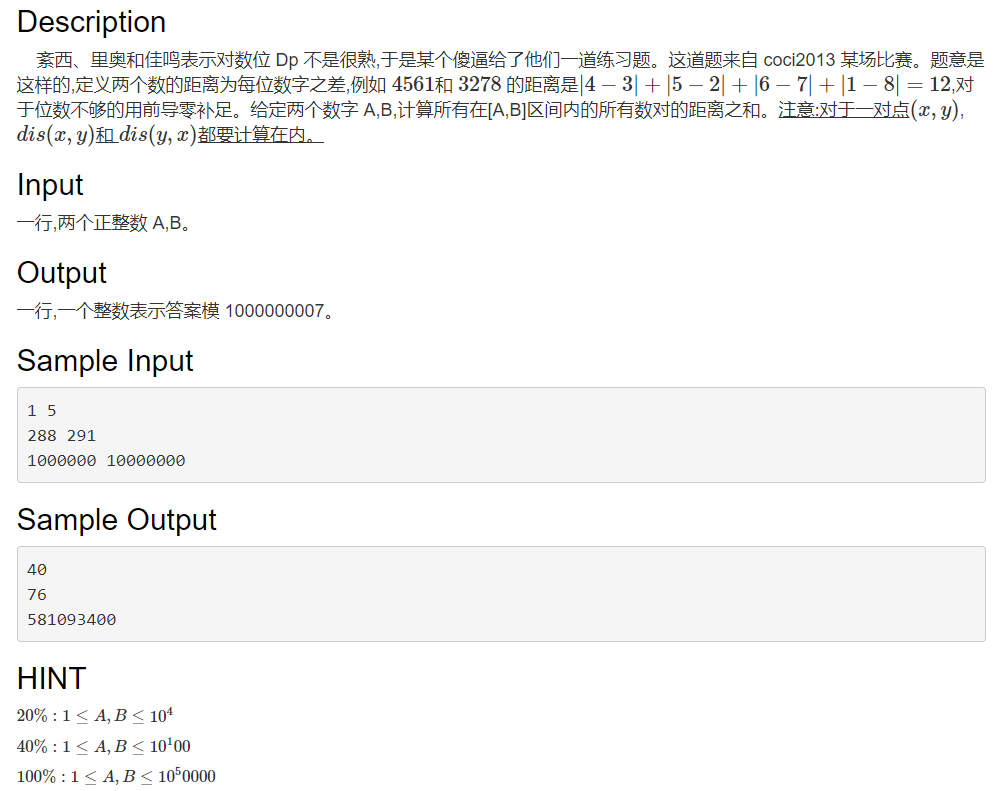
这题是显然的数位$dp$,然而我居然写了一个下午!!!
我们不难想到差分,令$solve(x,y)$表示从第一个数字在区间$[0,x]$,第二个数字在区间$[0,y]$的答案。
不难发现题目中给了你一对$A$,$B$,答案显然为$solve(B,B)-2solve(A-1,B)+solve(A-1,A-1)$。
考虑如何求解$solve(x,y)$函数,令$n=max(len(x),len(y))$,其中$len(p)$表示数字$p$在十进制下的长度(以下的位均代表十进制位)。
令$f[i]$表示数字$x$在模意义下前$i$位的值,令$F[i]$表示数字$x$在模意义下后$n-i+1$位的值。
同理,我们处理出$g[i]$和$G[i]$。
令$mi[i]$表示模意义下$10^i$的值,$Mi[i]$表示模意义下$10^(n-i+1)$的值。
令$ans[i][j][k]$表示第一个数字的第$i$位为$j$,第二个数字的第$i$位为$k$时的答案。
设第一个数字第$i$位为$j$的数字个数为$mul1$,第二个数字第$i$位为$k$的个数为$mul2$。
下面考虑如何求$mul1$,设$x[i]$为数字$x$的第i位,$num[i]$为数字$x$前$i$位构成的数,$Num[i]$为数字$x$后$i$位构成的数。
当$x[i]<j$时,$mul1=(f[i-1]+1)\times Mi[i+1]$,这里可以理解为前$i$位填一个数不大于$num[i-1]$的数,或者全填$0$,后$n-i$个数随便填的方案数。
当$x[i]==j$时,$mul1=f[i-1]\times Mi[i+1]+F[i+1]+1$ ,这里可以理解为前$i$位填一个小于$num[i-1]$的数,后$n-i$个数随便填的方案数,加上前$i$个数和$x$的前i个数相同,后n-i个数填写不大于F[i+1]的方案数。
当x[i]>j时,$mul1=f[i-1]\times Mi[i+1]$,这里可以理解为前$i$位填一个小于$num[i-1]$的数,后$n-i$位随便填的方案数。
求$mul2$同理
那么显然,$ans[i][j][k]=mul1\times mul2$。$solve(x,y)=\sum_{i=1}^{n}\sum_{j=0}^{9}\sum_{k=0}^{9}ans[i][j][k]$。
最终的答案为$solve(B,B)-2solve(A-1,B)+solve(A-1,A-1)$。考虑到$A$跟$B$的位数可能很大,这个减法需要用高精度。
完结撒花,注意细节。
1 #include<bits/stdc++.h> 2 #define MOD 1000000007 3 #define M 100005 4 #define LL long long 5 using namespace std; 6 char c[M]={0}; 7 struct bign{ 8 LL a[M+1],len; bign(){memset(a,0,sizeof(a));} 9 void rd(){ 10 scanf("%s",c); len=strlen(c); 11 for(LL i=0;i<len;i++) a[M-i]=c[len-i-1]-'0'; 12 } 13 void jian(){ 14 for(LL i=M,g=1;i&&g;i--){ 15 LL s=a[i]-g; 16 if(s>=0) a[i]=s,g=0; 17 else a[i]=s+10,g=1; 18 } 19 for(LL i=0;i<=M;i++) 20 if(a[i]!=0){ 21 len=M-i+1; 22 return; 23 } 24 } 25 }A,B,L,R; 26 LL f[M]={0},g[M]={0},F[M]={0},G[M]={0},mi[M]={0},Mi[M]={0},a[M]={0},b[M]={0},n; 27 28 LL solve(){ 29 n=max(A.len,B.len); LL res=0; 30 mi[0]=1; for(LL i=1;i<=n;i++) mi[i]=mi[i-1]*10%MOD; 31 F[n+1]=G[n+1]=0; 32 for(LL i=1;i<=n;i++) a[i]=A.a[M-n+i],b[i]=B.a[M-n+i]; 33 for(LL i=1;i<=n;i++) f[i]=(f[i-1]*10+a[i])%MOD,g[i]=(g[i-1]*10+b[i])%MOD; 34 for(LL i=n;i;i--) F[i]=(F[i+1]+a[i]*mi[n-i])%MOD,G[i]=(G[i+1]+b[i]*mi[n-i])%MOD; 35 Mi[n+1]=1; for(LL i=n;i;i--) Mi[i]=Mi[i+1]*10%MOD; 36 37 for(LL i=1;i<=n;i++){ 38 for(LL num1=0;num1<10;num1++) 39 for(LL num2=0;num2<10;num2++){ 40 LL cha=abs(num1-num2),mul1=0,mul2=0; 41 if(num1<a[i]) mul1=(f[i-1]+1)*mi[n-i]%MOD; 42 if(num1==a[i]) mul1=(f[i-1]*Mi[i+1]%MOD+F[i+1]+1)%MOD; 43 if(num1>a[i]) mul1=f[i-1]*Mi[i+1]%MOD; 44 45 if(num2<b[i]) mul2=(g[i-1]+1)*mi[n-i]%MOD; 46 if(num2==b[i]) mul2=(g[i-1]*Mi[i+1]%MOD+G[i+1]+1)%MOD; 47 if(num2>b[i]) mul2=g[i-1]*Mi[i+1]%MOD; 48 49 res=(res+mul1*mul2%MOD*cha)%MOD; 50 } 51 } 52 return res; 53 } 54 55 int main(){ 56 L.rd(); R.rd(); 57 LL ans=0; 58 A=R; B=R; 59 ans=solve(); 60 A=L; A.jian(); 61 ans=(ans-2*solve()+2*MOD)%MOD; 62 B=L; B.jian(); 63 ans=(ans+solve())%MOD; 64 cout<<ans<<endl; 65 }