Support Vector Machine(支持向量机详细解读)
I warm both hands before the fire of life.
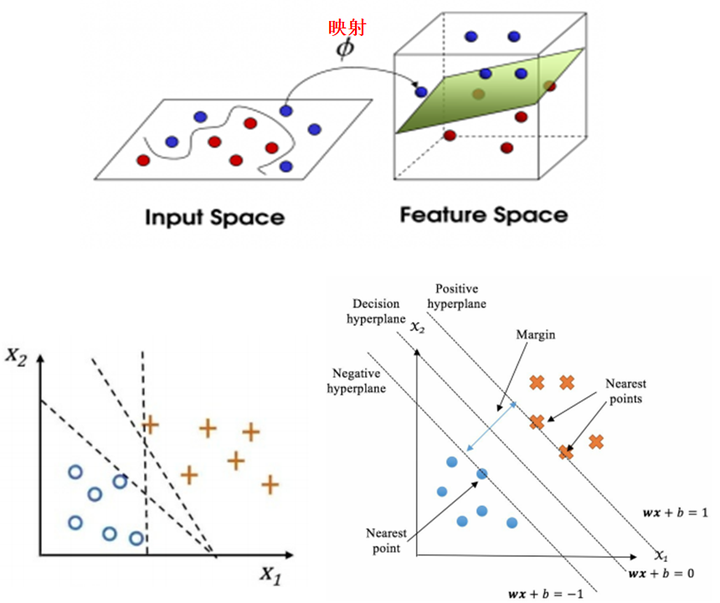
支持向量机:寻找最佳分隔的超平面;什么是最佳分隔?有两层意思,分别是高效映射(映射到可以分隔得“更好”的高纬空间)和分隔的间隔最大;
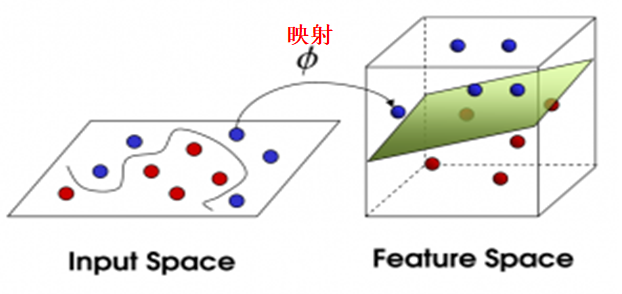
高效映射:原始数据在原空间中,不同样本混合程度高,不容易分隔,而将原数据高效映射到新空间,数据混合程度低,容易分隔,可以分隔得“更好”,如上图所示;

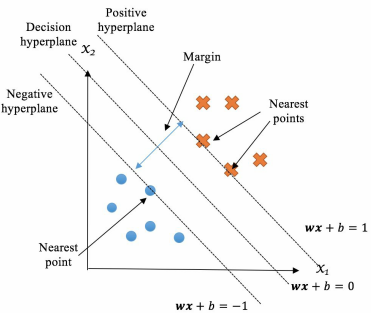
分隔的间隔最大:如上左图,样本中有两类点,分别是篮色O和黄色+;有很多条“线”可以将这两类点分开,但最佳的分隔只有一条如右上图,实现了最大间隔Margin;右上图中的最佳分隔wx+b=0其实是一个超平面(w是一个向量),支持向量机就是求解构成该超平面的w和b,其中离wx+b=0这个超平面最近的点代表的向量称为支持向量,即|wx+b|=1这两个超平面上所有的点代表的向量;
1. 高效映射
支持向量机做映射实现将原数据从原空间变换到新空间的新数据;此过程涉及两个问题,即映射和高效;
1.1 映射
假设原训练样本S是一个3X1000的矩阵,每一列代表一个训练样本,每个训练样本有2个特征值,则S=[S1,S2,...,S1000],其中Si是一个2维向量;映射后,新训练样本S'是一个1000X1000的矩阵,每一列是一个新样本点,每个新样本点有1000个特征,则S'=[ S'1,S'2,...,S'1000],其中S'i是一个1000维向量;
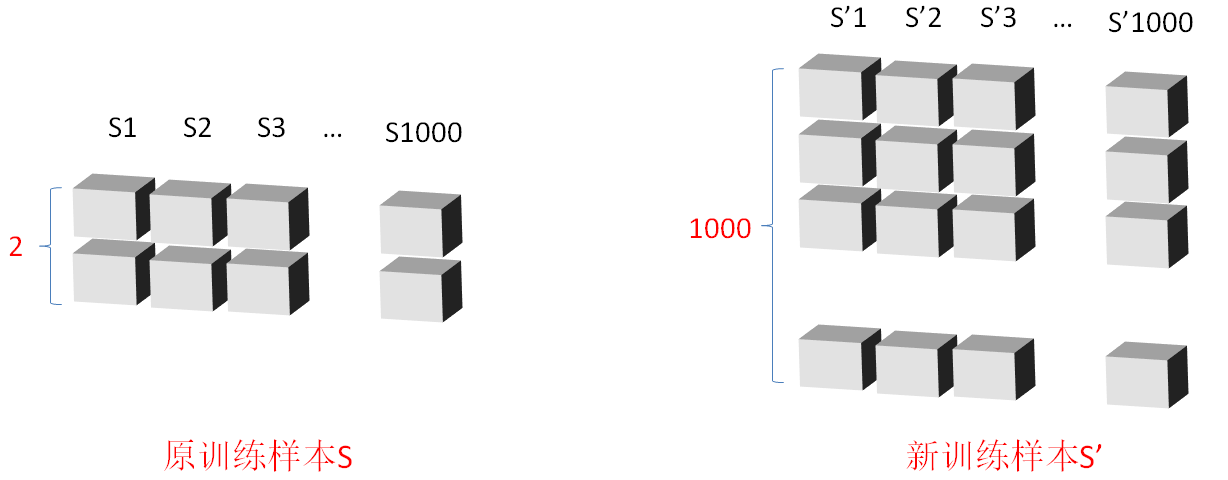
新训练样本的1000个特征是如何获得的?
取S'10=[x'1,x'2,x'3,...,x'1000]为例,其中x'1是原训练集中的S10和原训练集中的S1经过“特定运算”获取到的,x'2是S10和S2经过“特定运算”获取到的,以此类推,直到S'1000;
1.2 高效
如何实现高效?使用核函数;核函数有多种(仅列出如下几种),最常用的是高斯核函数;
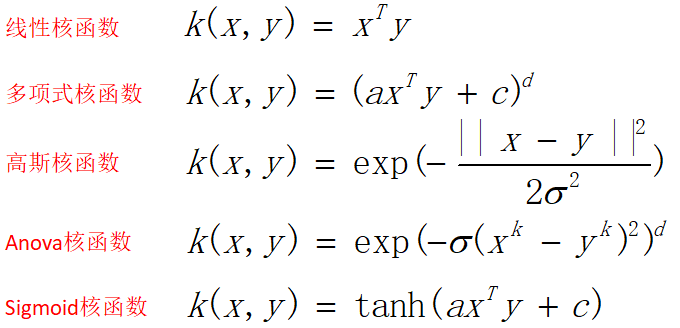
核函数是如何实现高效运算的?
以1.1中S'10的第一个元素x'1为例,x'1是由S10和S1经过“特定运算”获得的,S10=[x1,x2],S1=[y1,y2],有如下映射函数ø:
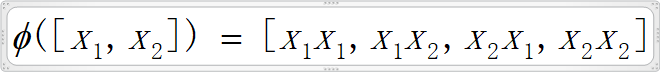
假设该“特定运算”是这样的:

即用映射函数ø实现该“特定运算”分为两步,首先是实现高纬映射(由2维映射到4维,每次映射需要4次乘法),该过程需要4*2次乘法(即两次映射);然后是点乘,需要4次乘法和3次加法;总共需要12次乘法和3次加法;
而该“特定运算”如果用核函数,此处选择多项式核函数,且设定多项式核函数中的参数a=1,d=2,c=0,即
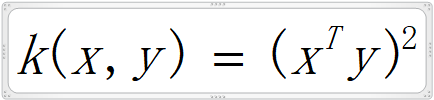
则由此核函数实现该“特定运算”如下:

该运算过程仅是点乘运算后平方,无映射过程;点乘需要2次乘法和1次加法;取平方需要1次乘法;总共需要3次乘法和1次加法;该运算量远小于上面通过映射函数ø映射到高纬空间后再点乘的运算量,而两者的结果是一样的;列举的样本数据仅仅是2维,如果是多维(即多个特征值),两种运算的差异会更明显;另外通过某些核函数如高斯核函数可以得到用普通映射函数需要升维到无限维后进行相关运算才能获得的特征值:
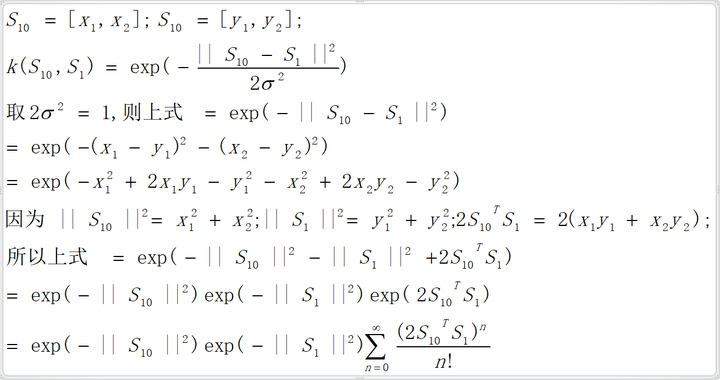
最后一步对exp(2S10TS1)泰勒级数展开,相当于普通映射函数对原2维数据映射到无穷维度后再累加;
2. 分隔的间距最大
2.1 间隔

取两个平行的超平面L+和L-使得这两个超平面之间没有训练样本点,但每个超平面上至少有一个训练样本点;则L+和L-两个超平面中间的超平面L;超平面L写为ax-c=0;则L-和L+可分别写为ax-c=-d和ax-c=d,且d>0;

在超平面L+:即wx+b=1上的一个点,对应的向量为X1;在超平面L-:即wx+b=-1上的一个点,对应的向量为X2;定义向量X3=X1-X2,如上图所示,X3在向量W方向上的投影即上图中的Margin;

现实分隔的间距最大,需要最大化Margin,即最小化||W||即可,且满足L+和L-两个超平面间没有样本点,L-超平面左下的样本点即蓝色O点加标值y=-1;L+超平面右上的样本点黄色+点加标值y=1;则对于每一个点的y(wx+b)的值应该大于等于1;则求分隔的间隔最大问题等价于以下优化问题--OptX:(其中||W||2=WTW):

2.2 求解OptX优化问题
两种方式:一种是通过凸二次规划直接求解;另一种是通过对偶问题转化求解;
2.2.1 通过凸二次规划直接求解
凸二次规划解决如下形式的问题,即如果需要求解的优化问题可以写成以下形式,则可带入求解器直接求解(python:cvxopt求解器):

设置上式中u、Q、t、ci、di的值如下:
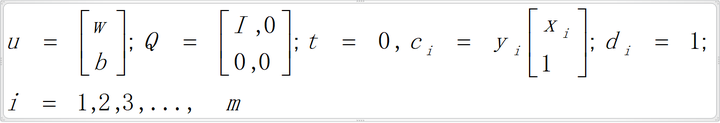
以上设置带入凸二次规划形式式子中即是优化问题OptX表达式,调用凸二次规划求解器可以直接求解,但是用对偶问题转化可以将问题简化;
2.2.2 通过对偶问题转化求解
2.2.2.1 拉格朗日函数
优化问题如下:
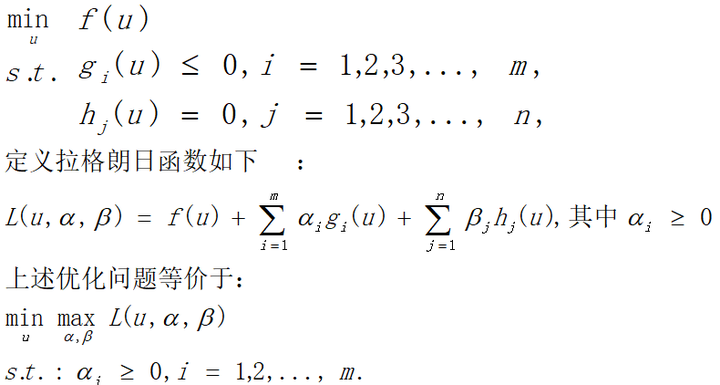
因为α≥0,调整参数α,β要使函数L可以取到max最大,则必满足g(u)≤0,否则α*g(u)的最大值将是正无穷(即无最大值);同样必须满足h(u)=0,否则β*h(u)最大值也将是正无穷(因为β可正可负);另外因为α≥0,且g(u)≤0,取α*g(u)要取最大值,则必须满足α*g(u)=0;所以要满足调整α,β要使函数L可取到最大除必定满足上述条件外,同时也使得函数L的后两项均为0,此时再调整参数u对函数L取最小,即相当于调整u对f(u)取min最小,即等价原优化问题;
2.2.2.2 对偶问题

当原优化问题为凸优化问题,即f和gi均为凸函数,hj为仿射函数,且可行域中至少有一点使不等式约束严格成立时,对偶问题等价于原问题;即函数L先调整α、β取最大再调整u取最小等价于函数L先调整u取最小再调整α、β取最大;
2.2.2.3 KKT条件(即拉格朗日函数在最优值处所满足的条件):

拉格朗日平稳性即朗格朗日函数对u的各个分量求偏导等于0;
2.2.2.3 支持向量机对偶型

该对偶问题即在满足α≥0时,先调整w、b使函数L取最小再调整α使函数L取最大;其中调整w、b使函数L取最小的过程没有限制条件约束(调整α使函数L取最大有α≥0约束),所以可以 通过L分别对w和b取偏导等于0实现消元;

将以上两个等式带入到函数L中,则对偶问题转化为新优化问题:


即新优化问题转换为以下形式:

2.2.2.4 支持向量机KKT条件
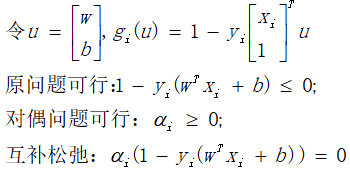
2.3 软间隔
以上2.2中针对的是训练样本可以完全分类,即wx+b=1超平面右上方没有任何蓝色O样本点,wx+b=-1超平面左下方没有任何黄色+样本点,且这两个超平面之间没有任何样本点;这种情况现实中很少出现,通常找到的超平面会存在分类错误的情况,这需要软间隔支持向量机,即允许在wx+b=-1超平面右上方出现蓝色O样本,允许在wx+b=-1超平面左下方出现黄色+样本;
2.3.1 软间隔支持向量机基本型
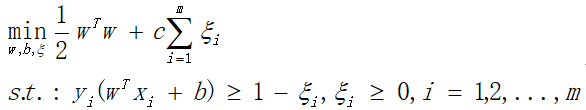
2.3.2 二次规划求解
以上优化问题属于二次规划问题,参数对应如下:
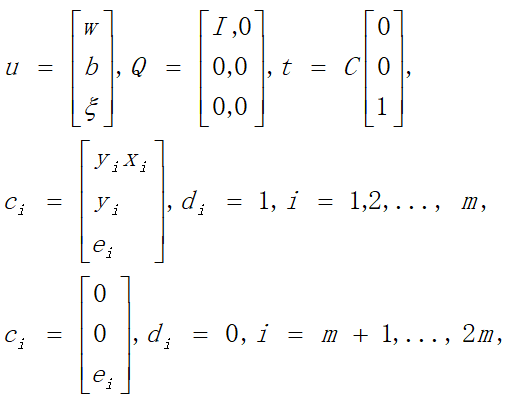
2.3.3 软间隔支持向量机拉格朗日函数
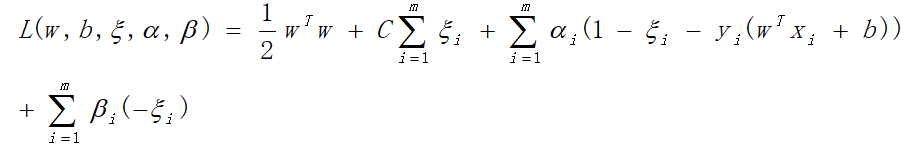
2.3.4 软间隔支持向量机对偶型


2.3.5 二次规划求解
以上软间隔支持向量机对偶型的优化问题属于二次规划问题,参数对应如下:
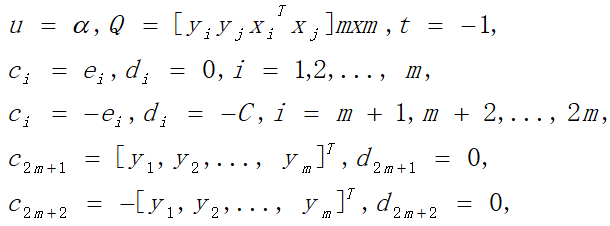
2.3.5软间隔支持向量机KKT条件

3. SMO优化算法
如上如果直接用凸二次规划求解器求解,特别面对训练样本很多时,其存储和计算开销很大,SMO序列最小化是一个利用支持向量机自身特性高效的优化算法;

该问题求解,即求满足约束条件情况下使软间隔支持向量机对偶型函数值最小的m个α值,其中m是样本数量;用凸二次规划求解器是一下求解所有α值,复杂度和计算量都很大,而SMO采用了一种启发式方法,每次只优化两个变量,将其它变量都视为常量(最小的可以每次只优化一个变量,但是受到
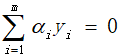
的限制,如果每次只优化一个变量,其它变量锁定,则该变量也是锁定的),假设选定的两个α分别是α1和α2,则最小化原函数等价于最小化原函数中仅与这两个α相关的项(其它项都是常数了),即:

针对上述两个限制条件,且y1和y2取值只能是1或者-1;这样α1和α2在[0,C]和[0,C]形成的盒子里面,并且两者的关系直线斜率只能是1或者-1;如下图:
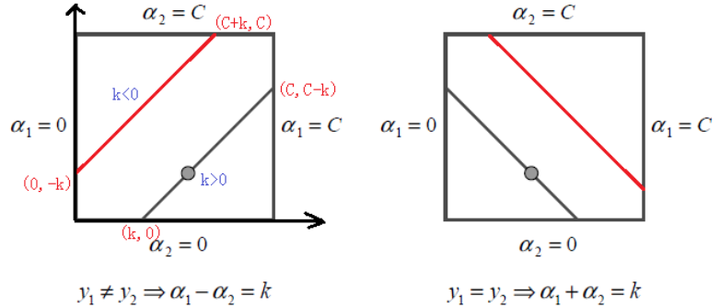
因为α1和α2两者有确定的线性关系
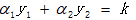
,所以可以用α1表示α2,则最终优化问题仅是关于一个参数(α2)的优化问题,则最终优化迭代出来的α2会有新的限制条件:L≤α2new≤H;

3.1 选择第一个α变量,即α1
SMO算法每次优化一对α变量,优化所有α变量对需要两层循环,其中第一个变量对应第一层循环,第二个变量对应第二层循环;
第一个变量α1选择训练集中违反KKT条件最严重的样本点,即违反以下条件:
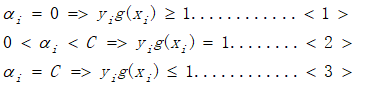
首先选择违反条件<1>的点,其次选择违反条件<2>和<3>的点;
3.2 选择第二个α变量,即α2
选择原则是与α1配对后在函数优化收敛过程中有最大的可修改范围;

3.3 求解选定的α对
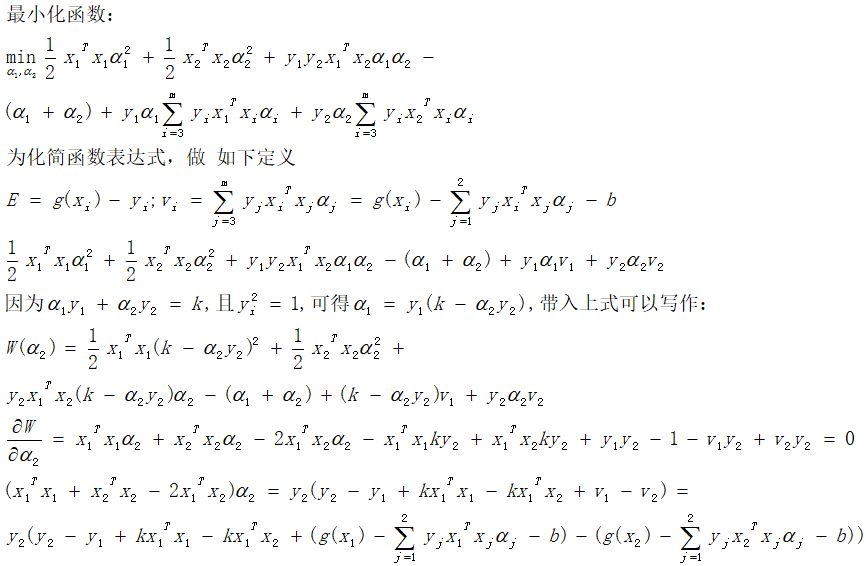
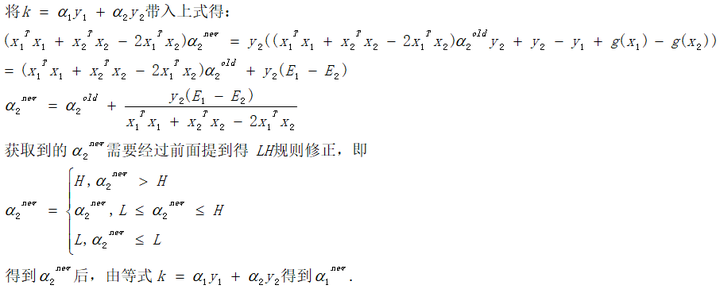
3.4 计算阈值b
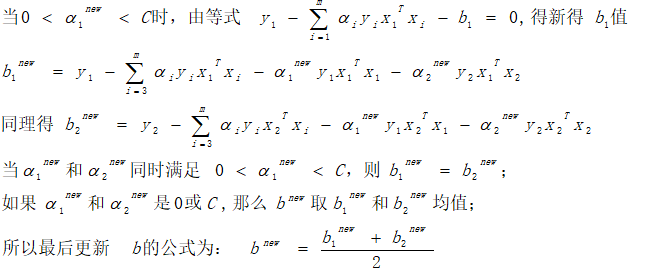
3.5总体优化:两层循环
初始化所有α变量值为0,第一层循环选定第一个变量,进入第二层循环选定第二个变量,开始计算两个变量及b的最新值,然后计算最小化函数值,如果选择的第二个点不能让最小化函数有足够的下降,则可以采用遍历支持向量点作为第二个点,直到最小化函数有足够的下降则跳出第二层循环;当在设定精度范围内满足如下条件,跳出第一层循环:

3.6 求解超平面

【转载】https://zhuanlan.zhihu.com/p/47100320
编辑于 19:21