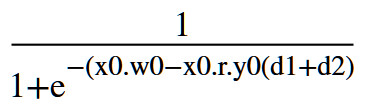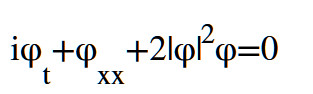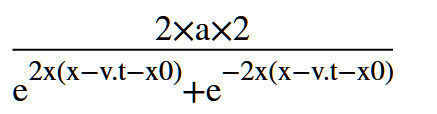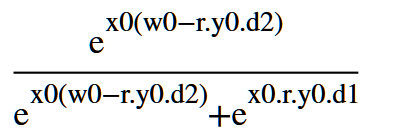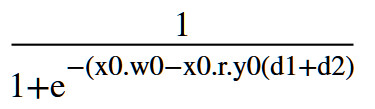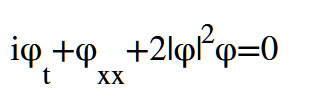神经网络有可能被公式化表达吗？

<用实验验证神经网络的节点是否可以看作弹性小球>中制作了一个1*1...1（共64个）的64层神经网络

for(inta=2 ;a<r-2 ;a++){          

d=x[a][0]*(x[a+1][0]-x[a+2][0])+x[a][0]*( x[a-1][0]-x[a-2][0]);

}

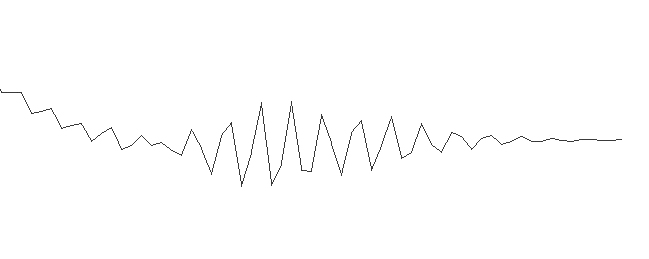
并让权重同时向前和向后收敛（首尾另做处理）得到的图像非常像水波

本文就由sigmoid的反向传导公式开始推导看看是否能和波函数有什么联系。

首先计算权重，以x5点为例，左边的w0可以看作是第二次传导的w5，右边的w0可以看作是第一次传导的w5，y3和y4对应图中的第一次正向传导得到的x6，x7。Y1，y2可以对应图中第一次正向传导得到的x4，x3。x0对应第一次正向时的初始的x5，y0对应第一次正向传导得到的x5

W0=w0-r[y0(y1-y2)+y0(y3-y4)]

W0=w0-r.y0[(y1-y2)+(y3-y4)]

Y1-y2=d1

Y3-y4=d2

W0=w0-r.y0(d1+d2)

r是学习率

由第一次反向传导得到的w0再一次计算y1

Y1=sigmoid[x0.w0-x0.r.y0(d1+d2)]

完整的写出来就是

式子可以化简成

 式A

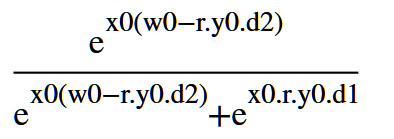
非线性薛定谔方程的最简单形式是

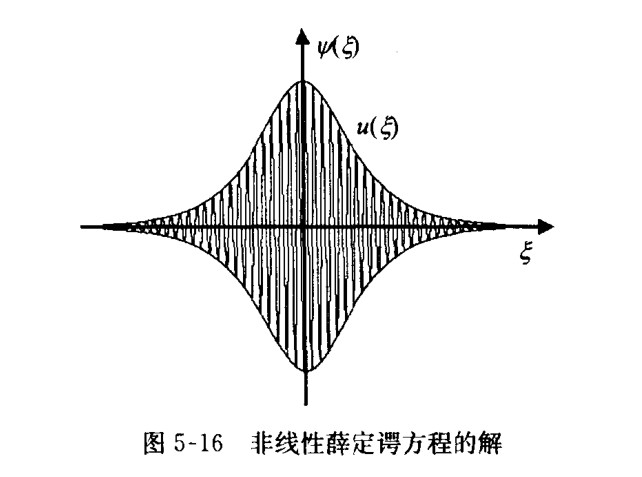
这个方程的解呈钟型

，解的方程是

a和x0是常数，是双曲正割曲线

展开

可以化简成

式B

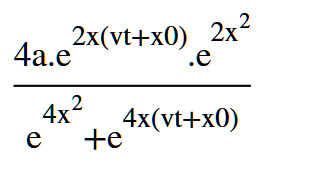
对比式A

假设可能有一种情况vt+x0无限接近x

也就是

让

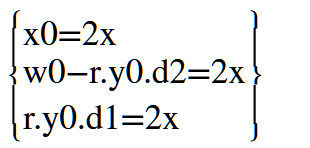
当满足

W0接近r.y0(d1+d2)

表达式

可以近似满足非线性薛定谔方程，

反向传导的sigmoid函数可能是非线性薛定谔方程的解。波幅越小越近似。