Manacher算法（求最长回文子串）

Manacher的主要用途是求一个字符串中包含的最长回文子串。

一、前期处理

1.原始字符串长度有奇有偶，为了方便处理字符串，我们使用了一种统一的处理方法。在每个字符两边都插入一个特殊字符（注意这个字符一定是原始字符串不包含的，否则就会混了）。
比如原始字符串是"abcba"，那增加特殊字符"#“之后就变成”#a#b#c#b#a#"；原始字符串是"abba"，增加特殊字符"#“之后就变成”#a#b#b#a#"。这样无论原始字符串长度是奇还是偶，处理之后都会变成奇数长度。
2.在增加特殊符号之后，为了方便地处理数组越界问题，我们在字符串头部再增加一个特殊字符（这个字符不在原始字符串内，也不能与初次添加的特殊字符相同），这样做的目的是在判定回文串时不可能越过0。
比如初次添加后字符串为"#a#b#c#b#a#"，我们可以再选用"@“作为二次特殊字符加到头部，这样字符串就变成”@#a#b#c#b#a#"。

为了讲解方便，我们先给出最终结果。
我们以字符串"12212321"为例，在前期处理之后字符串变为"@#1#2#2#1#2#3#2#1#"，记为S[i]，然后我们用一个数组P[i]来记录以i为中心的回文串的半径（包括i本身）。比如：

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
s[i]	@	#	1	#	2	#	2	#	1	#	2	#	3	#	2	#	1	#
P[i]	-	1	2	1	2	5	2	1	4	1	2	1	6	1	2	1	2	1

max(P[i]-1)就是最长回文子串的长度，我们下面来讲P[i]怎么求。

二、关于P[i]的说明

$\xi$ 记住P[i]就是以i为中心的回文半径!
首先P[i]的求解是从左到右的，也就是如果要求P[i]，那P[1]~P[i-1]已经求出来了，其中P[0]是越界指标不用考虑和计算。
P[i]指的是包括i本身在内的回文串半径，也就是说P[i]最小是1，因为只有一个字符也算回文串。比如检测到了回文串"#2#3#2#"，其中3为中心，那P[i]=4。

三、辅助变量

（1）id
id表示的是当前探测到的回文子串的中心点。
$id变换的条件是新检测到的回文串超出了当前回文串的范围。$
（2）mx
mx表示的是当前探测到的回文子串的右边界（不是边界本身，而是最右值+1）。
$mx的计算方法是mx=i+P[i]。$

我们来分析一下上图的示例。
当i=1时，令P[i]=1，然后看i+1和i-1是否相等，发现不等，判定结束。所以P[i]=1，此时id=1,mx=2。
当i=2时，令P[i]=1，然后看i+1和i-1是否相等，发现相等，P[i]+=1，然后看i+2和i-2是否相等，发现不等，判定结束。我们得到一个回文串"#1#"，P[i]=2，此时新的回文串右边界为4，超过了原来的mx，所以我们需要更新id=2，mx=4。
当i=3时，P[i]=1，此时新的右边界为4，没有超过mx，所以id和mx不更新。
当i=4时，我们检测到新的回文串"#2#"，P[i]=2，此时新的回文串右边界为6，超过了原来的mx，所以我们需要更新id=4，mx=6。
当i=5时，我们检测到新的回文串"#1#2#2#1#2#"，P[i]=6，此时新的回文串右边界为11，超过了原来的mx，所以我们需要更新id=5，mx=11。
…

四、核心方法

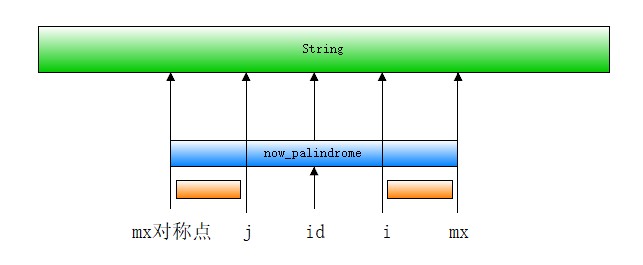
当你看上面的求解过程，你会觉得跟平常的回文串求解步骤是一样的。别急，下面就是Manacher的优化的地方了。先上图。
在这里插入图片描述

当前我们探测到的回文串为now_palindrome，中心点为id，右边界为mx，左边界为mx相对于id的对称点，即2*id-mx。当我们检测完id，i向后移动的过程中，我们可以利用回文串的对称性来缩减运算。图中i相对于回文串中心id的对称点是j，也就是i+j=2*id，即j=2*id-i。
所以可以知道的一个情况是:
$在now\_palindrome的范围内，i和j的回文半径是相同的。$
我们分情况来解释这句话：
（1）j是回文串中心，左半径在now_palindrome内。也就是说以j为中心的回文串最左边没有超过mx的对称点，即左半径在图中橙色方块内。这时候由对称性可知P[i]=P[j]，这样我们就不用对i进行逐个比较了。
（2）j是回文串中心，但左半径超出了now_palindrome。这时候我们只能确定的一件事是以i为中心的回文串右半径至少到达了mx。也就是P[i]>=mx-i。至于超过mx的部分是否仍然对称，就需要我们去逐个判断了。这样我们节省了mx之内的判断步骤。

用数学表达式来写就是：
（1）j的左半径越界
$j-P[j]<=2*id-mx$ $2*id-i-P[j]<=2*id-mx$ $即mx-i<=P[j]$
这时先令P[i]=mx-i，也就是i的半径至少从i到mx这么长。然后比较mx和2*i-mx是否相等，如果相等P[i]加1，然后接着比较mx+1和2*i-mx-1是否相等，如果相等P[i]加1，这样一直比较直到遇到两个不相等的数，P[i]计算完毕。
（2）j的左半径不越界
$即mx-i>P[j]$
此时P[i]=P[j]。当然这时候如果你接着从i+P[i]的位置比较一定不相等，因为P[j]已经证实了这一点。

看到这的时候我们必须要理解一个前提：
$一旦id变换，i的移动过程就会重置。$
也就是我们讨论的是当id固定的时候，i的移动情况，但是实际过程中有可能i移动两下id就换了，这样当然i又会从id+1的位置开始判定；但还存在一种情况就是i移动到mx了，id仍然保持不变。
我们上面说过了id更换的条件是新检测到的回文串超出了原来回文串的范围，而当i移动到mx时，此时检测到的回文串肯定超出了原来的范围了，所以是相当于自然重置了。所以当i>=mx时，我们应该先令P[i]=1，然后逐个比较i+1和i-1，i+2和i-2……一直比较到两个数不相等，这样就能够计算出P[i]。

总结起来就是：

if(mx>i)
{
	if(mx-i<=P[j])
	{
		P[i]=mx-i
		比较mx和2*i-mx，mx+1和2*i-mx-1
	}
	else
	{
		P[i]=P[j]
		比较i+P[i]和i-P[i]//其实不用比较，由P[j]可知一定不等
	}
}
else
{
	P[i]=1;
	比较i+1和i-1,i+2和i-2……
}

你会发现无论什么情况，开始比较的位置一定都是i+P[i]，因为P[i]已经告诉我们i的半径探到哪了，所以这就为我们节省了时间，把代码优化一下就变成:

P[i]=mx>i?min(mx-i,P[2*id-i]):1;
while(S[i+P[i]]==S[i-P[i]])
	P[i]++;

可以看到我们用min(mx-i,P[2*id-i])统一了mx-i<=P[j]和mx-i>P[j]的情况。其实仔细想一下就能知道，如果j左半径探出去了，那P[i]=mx-i，此时mx-i<P[j]；如果j没探出去，那P[i]=P[j]，P[j]<mx-i。

五、总体代码

void Manacher(string str)
{
    string s=str;
    if(s=="")
        return ;
    for(int i=0;i<s.length();i+=2)//前期处理
        s.insert(i,1,'#');
    s="@"+s+"#";
    int P[s.length()];
    int id=0,mx=0;
    int max_num=0;//记录最大半径
    int max_id=0;//记录最大半径下标
    for(int i=1;i<s.length();i++)
    {
       P[i]=mx>i?min(P[2*id-i],mx-i):1;//初始赋值
       while(s[i+P[i]]==s[i-P[i]])//继续搜索P[i]之外的地方
            P[i]++;
       if(i+P[i]>mx)//判定id是否更新
       {
           mx=i+P[i];
           id=i;
       }
       if(P[i]>max_num)
       {
           max_num=P[i];
           max_id=i;
       }
    }
    cout<<"最长回文子串长度为:"<<max_num-1<<endl;
    cout<<"最长回文子串为:"<<str.substr((max_id-P[max_id])/2,max_num-1);
}