也不知道是什么时候开始,对于曾经学过的算法都不太用了
遇到区间修改,区间最值就知道用线段树,什么树状数组啊,st表啊都忘得差不多了
最近几次模考被卡翻了,于是又想起这些老朋友
来填个坑
首先我们要明确一点,树状数组只能维护求和,不能维护区间最值
树状数组利用了分治的思想,层数为logn,所以查询和修改都是logn,总复杂度为询问次数m乘logn
也就是mlogn,最关键的是和线段树比起来,常数要小得多,跑的飞快
而空间复杂度则是n的,只用开一维,还不用结构体
但是树状数组的应用范围也相对较小
通常分为两种
(1)单点修改+取件查询
(2)区间修改+单点查询
具体为什么,我们一会儿会说到
首先来张图片吧
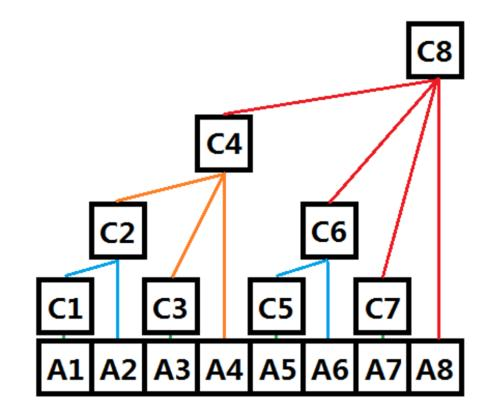
这是比较流行的一种图
显而易见,树状数组是上面的C数组,而下面的A则是全数组,练出来的线代表每个节点的值是由那几个点组成的
例如:C[4]=C[2]+C[3]+A[3]
而我们如何找到组成当前节点的每一个点呢,或者说如何找到当前点的父亲呢
这就引出了我们今天的重中之重
lowbit函数
来看一下这个函数长什么样子
int lowbit(int x){return x&(-x);}
对的,只要压一下行就只有一行的小小的函数,就是整个树状数组的核心了
虽然短,但是蕴含的内容却很不好理解,这个函数所求的是x化为二进制之后从末尾开始一共有几个零
x加上这个数之后,就得到了他的父亲节点的下标
减去这个数之后,就得到了上一个与x的子树不相交的根节点(因为建立是就是这样定义的)
具体的原因与二进制中的补码有关,我们在这里就不详细说了,当个模板来背即可
例如上图中,6+2=8 6-2=4
而这两种不同的运算也就对应了树状数组中的两种操作
操作一:单点修改
首先我们可以知道当前要修改的点在原数组中的下标i,同时知道要加上(减去)的值v
根据lowbit函数的定义我们可以知道,包含原数组中的值的节点的下标不可能小于原数组的下标
同时改变某个点的值只会对其父亲有影响,所以理所应当的加上lowbit(i),直到根节点
对于经过的每个节点,将权值加上v
void build(int i,int v){for(;i<=n;i+=lowbit(i)) c[i]+=v;}
同样是压行之后只有一行
操作二:区间查询
和树状数组的含义有关,当前的树状数组中存的是类似于前缀和的东西
所以我们很难得到一段区间的值,但是我们可以知道从1到x的值
假设要查询的区间为[x,y],我们可以得到a[1]+a[2]+……+a[x-1],也可以同理得1到y
做一下差会可以了
具体的实现流程就是从当前点开始,不断减去lowit(i),知道节点1,将路径上的每一个点的值累加
特别一题,树状数组中的下标不能为0,否则lowbit函数就会炸掉
放一下操作代码(同样很简洁,这也是树状数组的优点之一)
int solve(int i){ int sum=0; for(;i>=1;i-=lowbit(i)) sum+=c[i]; return sum; }
以上就是树状数组的单点修改和区间查询
来一道完整的题:树状数组模板1
附上AC代码:
#include<iostream> #include<cmath> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> using namespace std; inline int min(int a,int b){return a<b?a:b;} inline int max(int a,int b){return a>b?a:b;} inline int rd(){ int x=0,f=1; char ch=getchar(); for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1; for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0'; return x*f; } inline void write(int x){ if(x<0) putchar('-'),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); return ; } int n,m; int c[500006]; int lowbit(int x){return x&(-x);} void build(int i,int v){for(;i<=n;i+=lowbit(i)) c[i]+=v;} int solve(int i){ int sum=0; for(;i>=1;i-=lowbit(i)) sum+=c[i]; return sum; } int main(){ n=rd(),m=rd(); for(int i=1;i<=n;i++){ int x=rd(); build(i,x); } for(int i=1;i<=m;i++){ int f=rd(); int x=rd(),y=rd(); if(f==1) build(x,y); else write(solve(y)-solve(x-1)),puts(""); } return 0; }
然后就是一个小小的修改了
如何用树状数组来维护区间修改+单点查询
大家可以先自己想一想(反正我当时是没有想出来的)
不太会的同学不要担心
因为这里的树状数组和我们刚才讲的不太一样
哪里不一样呢,就是这里的C数组不是用来存和的
而是被用来存一个叫做差分的东西
什么是差分呢,就是对于一个数组
我们不维护每个地方的值,而是维护一个前缀和
使得从下标1加到下标x,就刚好可以得到原组的第x个元素
虽然查询变慢了,但是区间修改只需要O(1)的时间
为什么如此神奇呢,我们来举个例子
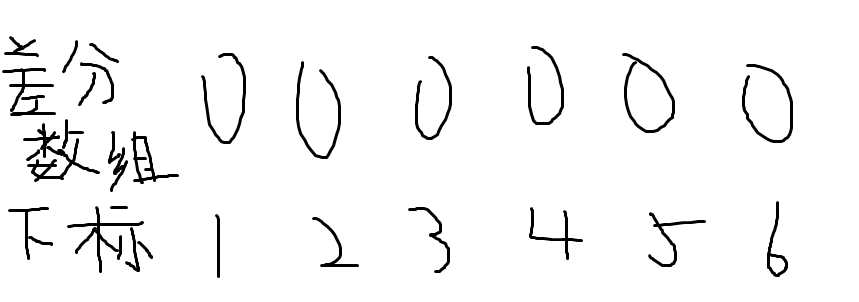
现在我们需要将2到4的区间加上1
我们就把差分数组下标为2的地方加1,下标为4+1的地方减1
就变成了:

计算前缀和,得到序列0 1 1 1 0 0 和原数组保持一致
是不是很神奇呢
而区间修改则是用树状数组来维护差分
虽然把修改变成了logn
但是相应的,单点查询也变成了logn
看似血亏,实则血赚
经过了上文的讲解,这里的具体操作我就不赘述了
再来一道题:树状数组模板2
附上AC代码:
#include<iostream> #include<cmath> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> using namespace std; inline int min(int a,int b){return a<b?a:b;} inline int max(int a,int b){return a>b?a:b;} inline int rd(){ int x=0,f=1; char ch=getchar(); for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1; for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0'; return x*f; } inline void write(int x){ if(x<0) putchar('-'),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); return ; } int n,m; int c[500006]; int lowbit(int x){return x&(-x);} void build(int i,int v){for(;i<=n;i+=lowbit(i)) c[i]+=v;} int solve(int i){ int sum=0; for(;i>=1;i-=lowbit(i)) sum+=c[i]; return sum; } int main(){ n=rd(),m=rd(); int set=0; for(int i=1;i<=n;i++){ int x=rd(); build(i,x-set); set=x; } for(int i=1;i<=m;i++){ int f=rd(); if(f==1){ int x=rd(),y=rd(),k=rd(); build(x,k);build(y+1,-k); } else{ int x=rd(); write(solve(x)),puts(""); } } return 0; }
总而言之,树状数组还是很好的一种数据结构
只要利用得当,每一种数据结构都能够焕发出耀眼的光芒,给代码带来无限生机