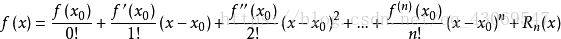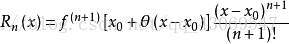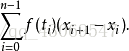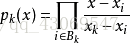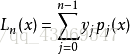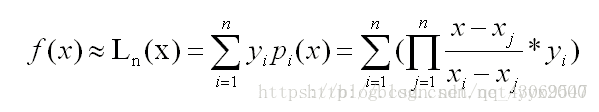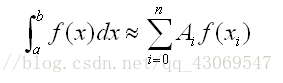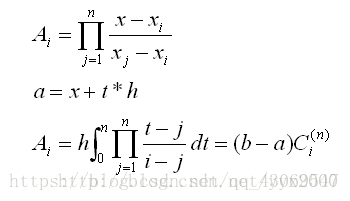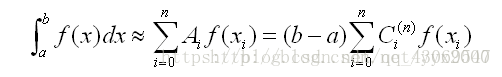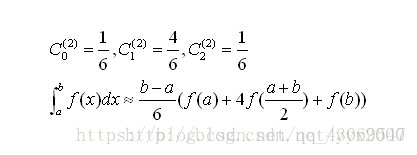数学分析中的泰勒公式告诉我们,对任何函数,我们都可以用多项式函数去逼近它的函数值,且对于解析性质很好的函数(例如任意阶可导+任意阶导函数有界),我们可以将误差缩小到任意小。
其中
那么,我们在求解析式复杂或者可能无法用初等函数表示原函数的积分问题时,能否也可以用多项式函数来代替呢?
辛普森公式就是用来做这样一件事情。
首先,我们先来确定用什么样的多项式函数去替换我们的原函数。由积分第一中值定理可得:
中值定理表明对于求定积分,我们可以用函数在区间中的某点函数值来乘以区间长度得到。事实上,定积分的定义也是类似的形式,只不过是一个无穷和的极限(黎曼和)
那么,如果我们已知区间中函数在若干点的函数值,我们怎样近似计算定积分呢?
一种朴素的思想是将函数值直接代入黎曼和,但这样的误差会很大。
其次,我们可以考虑一个多项式函数,用多项式函数的积分值来代替原函数的积分。而这样的多项式想要很好地逼近,自然是要在已知点的函数值与原来的函数相同。由拉格朗日插值公式可知,当次数与给定点数相同的情况下,这样的多项式是唯一确定的。
因此,对上述拉格朗日多项式求积分,即可得到原来函数的积分的近似值。而且,自然地,我们选取的点越多,其所得到的结果就越精确。(事实上,其代数精度至少为n,n为多项式次数)。
对上述多项式求积分后,可以发现,其积分恰好是原来的函数在给定点的函数值的线性组合,这样我们就达到了目的!接下来要做的是如何确定各函数值的系数。
对等式两边同时求积分得
将系数继续写出来:
(b-a)的系数叫做柯特斯系数。我们的到的定积分公式就是:
上述公式就是牛顿-柯特斯求积公式 。可是,虽然我们成功地用多项式函数的积分来替代原来函数的积分,并保持了满意的精度。但当n很大时,我们的得到的公式明显不易计算,为了兼顾精度与效率,可以取n=3,则x1=a,x2=(a+b)/2,x3=b。此时得到的就是辛普森公式,它拥有不错的精度(代数精度为3),而且方便记忆,易于计算。
辛普森公式本质上就是用二次曲线来逼近函数,在理论计算时我们可以将积分上下限分成若干个小区间,在每个区间内用辛普森公式来近似计算。编程时可以利用函数的递归调用,让计算机帮助我们自动划分区间,当检测到区间二分后的误差在精度范围内后就可对区间停止二分输出结果。最后的积分值就是所有小区间的近似值的和。
下面是代码。
double simpson(double a,double b)//辛普森公式
{
double c = a + (b − a)/2;
return (F(a) + 4*F(c) + F(b))*(b − a)/6;
}
double asr(double a,double b,double eps,double A)//A为本区间的辛普森公式计算的值
{
double c = a + (b − a)/2;
double L = simpson(a,c), R = simpson(c,b);
if(fabs(L + R − A) <= 15*eps)return L + R + (L + R − A)/15.0;//子区间的误差小于精度,停止递归。
return asr(a,c,eps/2,L) + asr(c,b,eps/2,R);
}
double asr(double a,double b,double eps)
{
return asr(a,b,eps,simpson(a,b));
}