【Leetcode】【DP】 72. Edit Distance / 编辑距离

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

Insert a character
Delete a character
Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

给定两个字符串，求编辑距离。编辑距离即是对字符串进行：删除一个字符，插入一个字符，替换一个字符的操作，每个操作计数1，从字符串1到字符串2的操作数即为编辑距离。

可画图分析：

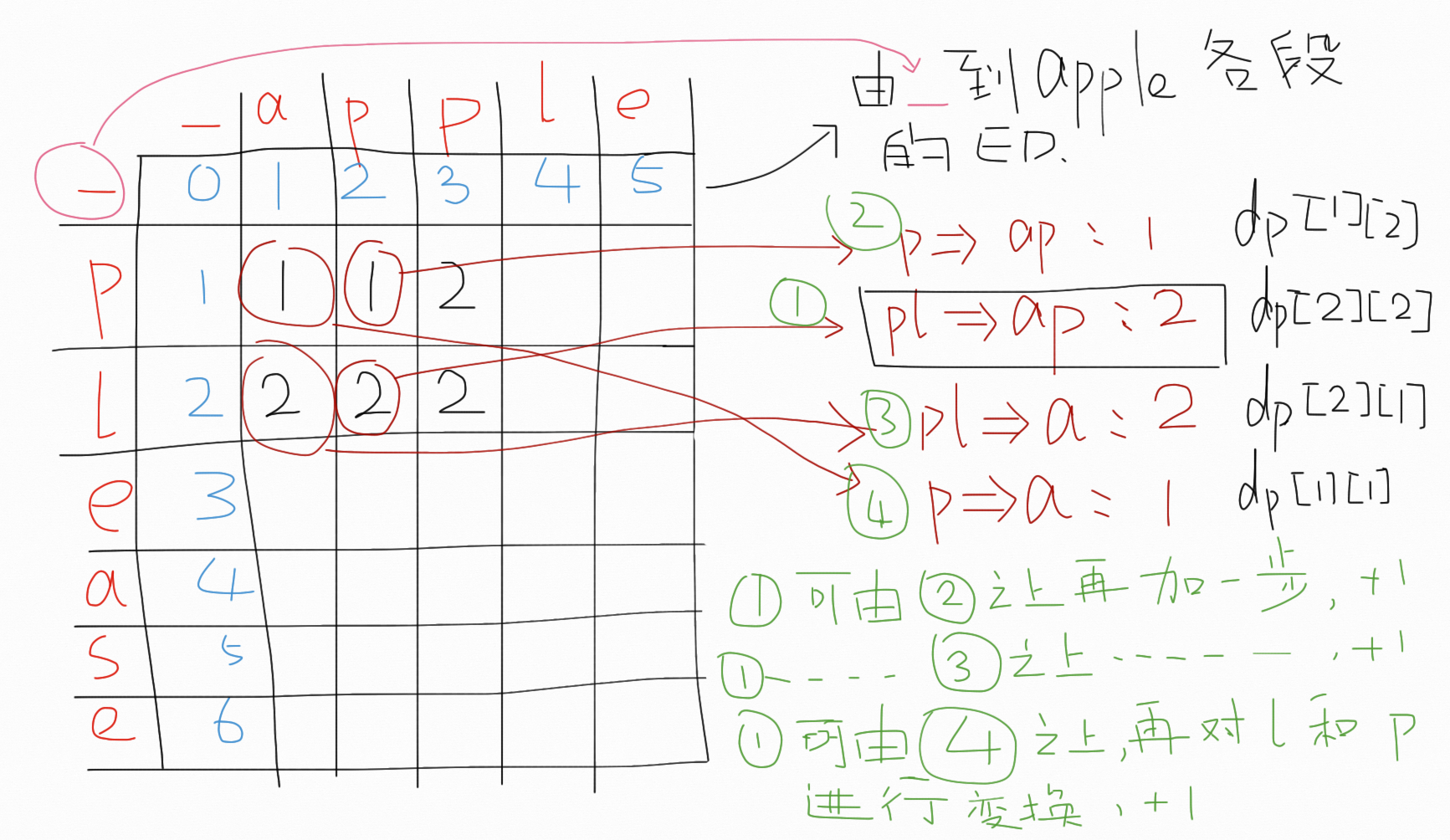
如，由字符串A：please 和字符串B：apple。长度为m和n。

首先构建一个 (m+1) x (n+1) 的二维数组，定义 dp [i][j] 表示字符串A的前i个组成的子字符串和字符串B的前j个组成的子字符串的编辑距离。

dp[i][j] （此处取dp[2][2]，即 pl 和 ap ）分析如下：

首先之前已经求得了dp [2-1] [2] （p和ap的编辑距离），dp [2] [2-1] （pl和a）, dp [2-1] [2-1] （p和a）。

pl -> ap 可先 ap -> p (等同于p->ap) ，再加上一个 插入l 的操作，即为 dp [1] [2] + 1 ,扩展为 dp [i] [j] = dp [i-1] [j] + 1
pl -> ap 可先 pl -> a ，再加上一个 插入p 的操作，即为 dp [2] [1] + 1 ,扩展为 dp [i] [j] = dp [i] [j-1] + 1
pl -> ap 可先 p -> a ，再加上一个 将 l 换为 p 的操作，即为 dp [1] [1] + 1 ,扩展为 dp [i] [j] = dp [i-1] [j-1] + 1。但如果替换操作中的A[2] = B[2]，如 pl -> al 的操作，p -> a ，再加上一个 将 l 换为 l 的操作，即无需操作，dp [1] [1] + 0 ,扩展为 dp [i] [j] = dp [i-1] [j-1] + 0。定义这个0/1操作数为cost，if A[i] == B[j] , cost = 0，否则cost = 1。dp [i] [j] = dp [i-1] [j-1] + cost

综上，欲得到最小编辑距离，dp = 三种情况的最小值。

故进行以下几步：

构建 (m+1) x (n+1) 的二维数组
初始状态：第一行（由A空字符串到B的编辑距离）/第一行。
由dp公式递推
返回最右下值

总公式:

    int minDistance(string word1, string word2) {
        int m = word1.size();
        int n = word2.size();
        if(m==0 || n==0)
            return m+n;
        vector<vector<int>> dp(m+1, vector<int>(n+1, 0));
        
        for(int i=0; i<=n; i++) {
            dp[0][i] = i;
        }
        for(int i=0; i<=m; i++) {
            dp[i][0] = i;
        }
        int cost = 0;
        for(int i=1; i<=m; i++) {
            for(int j=1; j<=n; j++) { 
                if(word1[i-1] == word2[j-1])    // 此处检查word1的当前字符和word2的当前字符是否相等
                    cost = 0;  // 相等则说明，当前段的编辑转换 等于 从word1的前一段转换到word2的前一段
                else 
                    cost = 1;  // 否则需要进行一次转换操作，即已知A和B的前一段转换需要x操作，则当前需要再对后面这个字母进行一次替换操作
                dp[i][j] = min(dp[i-1][j-1]+cost, min(dp[i-1][j]+1, dp[i][j-1]+1));
            }
        }
        return dp[m][n]; // 矩阵为 m+1 x n+1， 故最终返回dp[m][n]
    }

易错处：

dp初始化时需要先将第一行第一列初始化，因为后续递推式有 i-1 和 j-1 项。

dp长度时 m+1，n+1的，记住循环的边界在 i<=m，j<=n。以及最后返回值是dp[m][n]

求三项最小值应用两个min组合来得到

【Leetcode】【DP】 72. Edit Distance / 编辑距离

猜你喜欢