神经网络（三）：神经网络

版权声明：本文为作者唐亘的原创文章，欢迎转载，但请注明出处。 https://blog.csdn.net/weixin_39844018/article/details/82936318

一、 神经元到神经网络

在之前的文章中（《神经网络（一）》和《神经网络（二）》），我们讨论了如何为神经元搭建模型。虽然搭建模型的过程并不复杂，但得到的神经元模型也没有太多的新意，比如使用sigmoid函数作为激活函数，则得到的神经元模型就是逻辑回归。

在人体中，单个神经元能做的事情非常有限，但多个神经元相互交织在一起就组成了人类强大的神经系统。这启发我们需要将多个神经元模型联结起来组成复杂的神经网络，而这正是这篇文章讨论的重点。

二、 图形表示

将多个神经元联结起来最简单且最直观的方法就是将它们首尾相接形成一个没有环的网络（acyclic graph），在这个网络中，一个神经元的输出是另一个神经元的输入。这种类型的神经网络在学术上被称为人工神经网络（Artificial Neural Networks，ANN） ¹，它的模型拓扑结构如图1所示。

在神经网络中，神经元是按层（layer）组织的。每一层包含若干个神经元，层内部的神经元是相互独立的，也就是说它们之间并不相连；但相邻的两层之间是全连接的（fully-connected），也就是说任意两个神经元都是直接相连的（当然前提是这两个神经元分别来自相邻的两层）。

神经网络中不同的层按功能分为3类，分别是输入层（input layer）、隐藏层（hidden layer）以及输出层（output layer）。

1. 神经网络里只有一个输入层，其中的元素在图中标记1里用黑色的点表示：一个黑点表示一个模型的输入，也就是训练数据里的一个自变量，若训练数据有个特征，则输入层里一定有相应的个点。在模型中，输入层对数据不做任何处理，只负责将信息传递给后面的隐藏层（若网络里没有隐藏层，则将信息直接传递给输出层，这时候，神经网络其实就是逻辑回归）。

2. 神经网络可以有多个隐藏层，比如图1中就有两个隐藏层。隐藏层里的元素就是之前讨论的神经元模型（更具体一点，它们都是sigmoid神经元），因此在图中标记1里用圆圈表示。值得注意的是，一个圆圈包含了线性模型以及激活函数。在多层感知器里，隐藏层的作用是传输并分析数据。

3. 神经网络里只有一个输出层。输出层里的元素与隐藏层里的不同，它只包含线性模型，因此在图中标记1里用方块表示。虽然输出层的名字里有“输出”二字，但它并不是模型的最终输出，与《神经网络（二）》中的逻辑回归类似，输出层的结果经过softmax函数处理后，才能得到最终的模型结果（如果该神经网络解决的是分类问题）。

图1

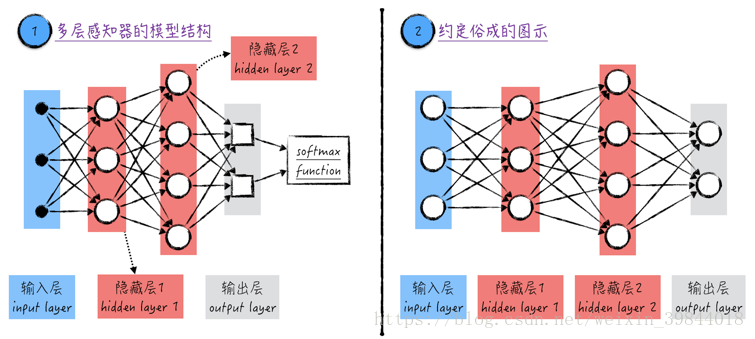
正如上面讨论的，不同层里的元素是不一样的，但对于神经网络领域，大家约定俗成地都用圆圈来表示它们，也将它们统称为神经元（虽然这样很容易给初学者造成误解），并将最后一步的softmax函数省略掉，如图1中标记2所示。

1. 图1中的标记1和标记2表示的同样的神经网络，其中标记2中的图示在神经网络领域是通用的，因此在之后的章节中我们将沿用这样的记号。

2. 对于神经网络，通常会以它所拥有的层数来命名，但这时输入层是不计算在内的，比如图1中的模型被称为3-层神经网络（3-layer neural networks）。当然这样的命名并不能唯一地标识一个神经网络，比如将图1中的隐藏层1增加到10个神经元，得到的仍然是一个3-层神经网络。

三、 数学基础

神经网络在图形上的表示是比较直观的，但它所代表的数学公式却是极其复杂的。为了更深入地理解神经网络，下面将讨论图形背后的数学基础。

为了讨论方便，我们来看一个非常简单的2-层神经网络（假设这个神经网络用于解决分类问题），如图2所示。

图2

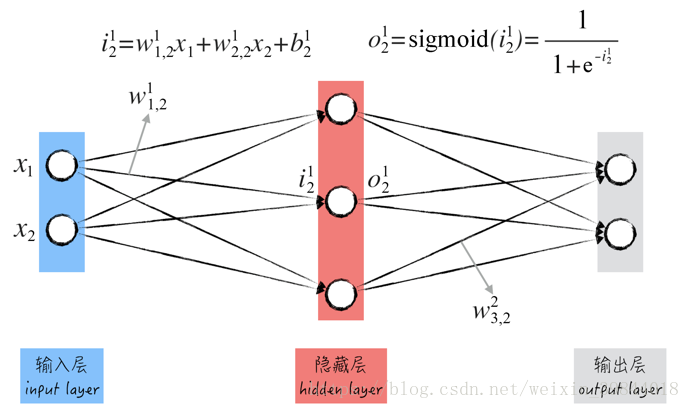
这个网络的输入层有两个圆圈，表示模型所用的两个自变量，分别用 $x_1, x_2$表示。

隐藏层里的圆圈表示神经元模型，它包含两个部分：线性模型和激活函数。

1. 对于第 $l$层（从左到右编号）里的第 $m$个神经元（从上到下编号），用记号 $i^l_m$表示相应的线性模型输出（圆圈输入的第一层加工），用记号 $o_m^l$表示激活函数的输出（也是圆圈的输出）。由于这个神经网络里都是sigmoid神经元，因此两者之间的关系如公式（1）所示。

$o^l_m = \frac{1}{1 + e^{-i^l_m}}\tag{1}$

2. 图中圆圈之间的箭头表示线性模型中的权重（这是神经网络的一部分模型参数），用记号 $w_{m, n}^l$表示从第 $l - 1$层里第 $m$个圆圈到第 $l$层里第 $n$个圆圈的箭头，比如图2中的 $w_{1, 2}^1$和 $w_{3, 1}^2$。值得注意的是，为了书写方便，我们将输入层记为第0层。

3. 除了权重之外，线性模型里还有一个截距项（这是神经网络的另一部分模型参数），用记号 $b_m^l$表示第 $l$层里第 $m$个圆圈所对应的截距。结合上面的记号，圆圈里线性模型的输出公式如下。值得注意的是， $o_m^0$表示输入层里第 $m$个自变量，也就是图中的 $x_m$。

$i_n^l = \sum_m w_{m, n}^lo_m^{l - 1} + b_n^l\tag{2}$

输出层的圆圈只表示线性模型，虽然圆圈里并没有激活函数，但为了书写简单，依然用记号 $o_m^2$表示图2里输出层圆圈的输出。

1. 与隐藏层有所不同，在输出层里，我们有 $i_m^l = o_m^l$（ $i_m^l$的计算公式与隐藏层中的一模一样，在此不再赘述）。

2. 针对分类问题，相应的损失函数如公式（3）所示。其中 $\sigma$为《神经网络（二）》中讨论过的softmax函数； $Z_i = (o_1^2, o_2^2)_i$表示针对第 $i$个数据的神经网络输出； $\theta_i$表示的第 $i$个数据的类别，如果是类别0，则 $\theta_i = (1, 0)$，否则 $\theta_i = (0, 1)$。

$L = \sum_i L_i = -\sum_i\theta_i\ln\sigma(Z_i)^T\tag{3}$

将上面的讨论总结一下，神经网络的模型参数分为两类：一类是线性模型的权重 $w_{m, n}^l$，在图2中，一共有 $3 \times 2 + 2 \times 3 = 12$个这样的参数；一类是线性模型的截距项 $b_m^l$，在图2中，一共有5个这样的参数。由此可见，神经网络的模型参数是很多的，而且与其他模型有所区别的是，它的模型参数是明显分层的。也就是说，从数学上来看，神经网络的模型参数是前后依赖的。这使得神经网络的训练变得十分复杂，需要使用比较特殊的算法来（反向传播算法）估算模型参数。这部分内容将在之后的文章中仔细讨论。

四、广告时间

这篇文章的大部分内容参考自我的新书《精通数据科学：从线性回归到深度学习》。

李国杰院士和韩家炜教授在读过此书后，亲自为其作序，欢迎大家购买。

另外，与之相关的免费视频课程请关注这个链接

---

1. 在有些文献中，这样的神经网络又被称为多层感知器（Multi-Layer Perceptron，MLP） ↩︎