如何判断一个点在三角形内部

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/pdcxs007/article/details/51436483

如何判断一个点在三角形内部

基本思路

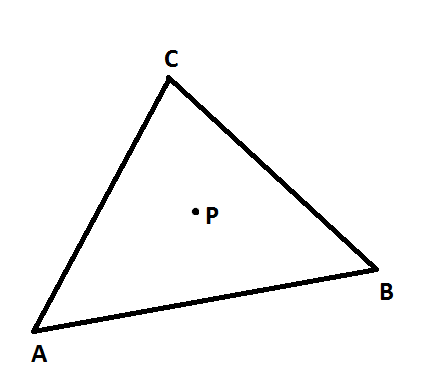
如图，点P在三角形ABC内部，可以通过以下三个条件判断：

1. 点P和点C在直线AB同侧
2. 点P和点B在直线AC同侧
3. 点P和点A在直线BC同侧

如果以上三个条件同时满足，则点P在三角形ABC内部。

下面将会用到叉乘这个数学工具来确定一个点在直线的哪一侧。

判断点在直线的哪一侧

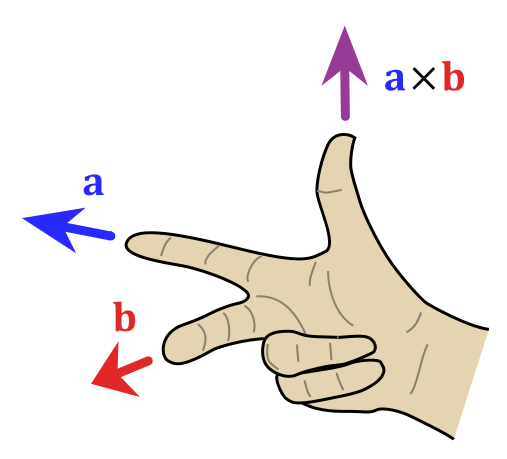
叉乘是一个判断点在直线哪一侧的数学工具。先看一下叉乘的定义：

$$\vec{a} \times \vec{b} = \| \vec{a}\| \| \vec{b} \| \sin \theta \vec{n}$$

其中，$\theta$为向量夹角，$\vec{n}$是一个向量，与$\vec{a}$和$\vec{b}$都垂直，方向满足右手螺旋法则，即下图所示：

于是，从第一个向量的方向看，如果第二个向量在左边，那个叉乘是正的，在右边，则是负的，在同一个方向上，则是0.叉乘的大小，则是两个向量组成的平行四边形的面积。

那么叉乘具体如何计算呢？先将x、y、z轴方向的单位向量分别记为$\vec{i}$、$\vec{j}$和$\vec{k}$，则如果有两个向量，分别为：

扫描二维码关注公众号，回复： 3381391 查看本文章

$$\vec{u}=u_1\vec{i}+u_2\vec{j}+u_3\vec{k} = (u_1, u_2, u_3) \\ \vec{v}=v_1\vec{i}+v_2\vec{j}+v_3\vec{k} = (v_1, v_2, v_3)$$
则有：
$$\vec{u}\times\vec{v}=(u_2v_3-u_3v_2)\vec{i}+(u_3v_1-u_1v_3)\vec{j}+(u_1v_2-u_2v_1)\vec{k}$$
可以用以下行列式来简记：
$$\vec{u}\times\vec{v}=\left| \begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ \end{matrix}\right|$$
如果叉乘的两个向量都是平面向量，则可以看作是第三个分量为0的三维向量。

以下Processing程序可以验证叉乘用于点在直线哪一侧的判断的正确性：

PVector a = new PVector(100, 200);
PVector b = new PVector(300, 300);
PVector c = PVector.sub(b, a);

void setup() {
  size(400, 400);
  fill(0);
}

void draw() {
  background(255);
  line(a.x, a.y, b.x, b.y);
  PVector d = new PVector(mouseX - a.x, mouseY - a.y);

  String side;
  if (c.cross(d).z > 0)
    side = "left";
  else if (c.cross(d).z < 0)
    side = "right";
  else
    side = "on";
  text(side, 40, 40);
}

有兴趣的读者也可以把cross方法展开试试。

算法实现

现在算法已经很明显啦！其中有一点小技巧，三角形的三个顶点是转着来的，算一次就行了。比如，在上图中，点C在直线AB左侧，点B在直线CA的左侧，点A在直接BC的左侧。所以，第一步是先计算三角形的方向：

float signOfTrig = (b.x - a.x)*(c.y - a.y) - (b.y - a.y)*(c.x - a.x);

注意这样一下子写出来不太容易看明白，但是如果看成向量AB和向量AC叉乘之后的Z坐标就好懂的多了。

再分别计算P在AB、CA、BC的哪一侧：

float signOfAB = (b.x - a.x)*(p.y - a.y) - (b.y - a.y)*(p.x - a.x);
float signOfCA = (a.x - c.x)*(p.y - c.y) - (a.y - c.y)*(p.x - c.x);
float signOfBC = (c.x - b.x)*(p.y - c.y) - (c.y - b.y)*(p.x - c.x);

最后判断它们是否在同一侧：

boolean d1 = (signOfAB * signOfTrig > 0);
boolean d2 = (signOfCA * signOfTrig > 0);
boolean d3 = (signOfBC * signOfTrig > 0);
println(d1 && d1 && d3);

这就是所有的算法了！最后来个程序验证一下。

验证程序

PVector[] trig;
float r = 150;
float t = 0;
float interval = 30;

void setup() {
  size(500, 500);
  trig = new PVector[3];
  ellipseMode(CENTER);
}

void draw() {
  translate(width/2, height/2);
  updateTrig();
  background(0);
  stroke(255);
  line(trig[0].x, trig[0].y, trig[1].x, trig[1].y);
  line(trig[1].x, trig[1].y, trig[2].x, trig[2].y);
  line(trig[0].x, trig[0].y, trig[2].x, trig[2].y);

  noStroke();
  for (float i = -width/2 + interval/2; i < width/2; i += interval) {
    for (float j = -height/2 + interval/2; j < height/2; j += interval) {
      if (inTrig(i, j)) {
        fill(255, 0, 0);
      } else {
        fill(255);
      }
      ellipse(i, j, 2, 2);
    }
  }
  t += 0.5;
}

void updateTrig() {
  for (int i = 0; i < 3; i++)
    trig[i] = new PVector(r * cos(radians(i * 120 + t)), r * sin(radians(i * 120 + t)));
}

boolean inTrig(float x, float y) {
  PVector a = trig[0];
  PVector b = trig[1];
  PVector c = trig[2];
  PVector p = new PVector(x, y);

  float signOfTrig = (b.x - a.x)*(c.y - a.y) - (b.y - a.y)*(c.x - a.x);
  float signOfAB = (b.x - a.x)*(p.y - a.y) - (b.y - a.y)*(p.x - a.x);
  float signOfCA = (a.x - c.x)*(p.y - c.y) - (a.y - c.y)*(p.x - c.x);
  float signOfBC = (c.x - b.x)*(p.y - c.y) - (c.y - b.y)*(p.x - c.x);

  boolean d1 = (signOfAB * signOfTrig > 0);
  boolean d2 = (signOfCA * signOfTrig > 0);
  boolean d3 = (signOfBC * signOfTrig > 0);

  return d1 && d2 && d3;
}

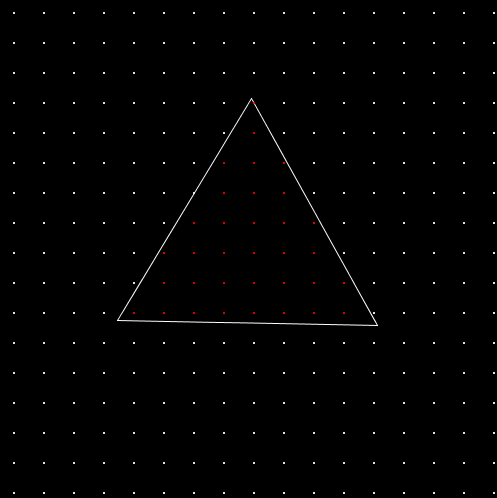
效果如下：