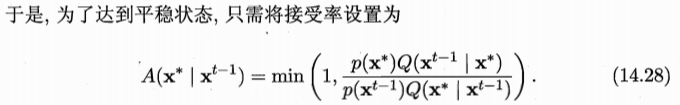题目:贝叶斯网络结构学习之MCMC算法(基于FullBNT-1.0.4的MATLAB实现)
有关贝叶斯网络结构学习的一基本概念可以参考:贝叶斯网络结构学习方法简介
有关函数输入输出参数的解释可以参考:贝叶斯网络结构学习若干问题解释
本篇所基于的马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)方法是一个通用的框架,其代表性的算法是Metropolis-Hastings(MH)算法,MH算法的特例Gibbs采样算法应用也很广泛。本文不具体探讨MCMC的细节,若想了解更多有关MCMC算法内容推荐参考【Bishop C M. Pattern Recognition and Machine Learning (Information Science and Statistics)[M]. Springer-Verlag New York, Inc. 2006.】(简称PRML)的11.2节(MarkovChain Monte Carlo),中文资料参考【周志华. 机器学习[M]. 清华大学出版社,2016.】(简称西瓜书)的14.5.1节(MCMC采样),Gibbs采样算法的细节可以参考PRML的11.3节(Gibbs Sampling),中文资料参考西瓜书的7.5.3节(推断),本文附录中会简要给出几个查阅文献时的关键点,但若想真正弄懂还须阅读推荐的文献资料。
将工具箱添加到matlab中的步骤参见上一篇《贝叶斯网络结构学习之K2算法(基于FullBNT-1.0.4的MATLAB实现)》的附录2,若仅想使用本文介绍的算法学得贝叶斯网络结构,可以在添加工具箱到Matlab中后,调用本文后面部分个人进行二次封装的函数:learn_struct_mcmc_basic.m,此函数仅需输入数据集,输出即为学得的网络结构。但是,建议大致浏览一遍全文。
据文献【胡春玲. 贝叶斯网络结构学习及其应用研究[D]. 合肥工业大学, 2011.】所述:将MH方法引入贝叶斯网络结构学习的文献有如下几篇:
[45] Friedman N, Koller D. Being Bayesianabout network structure. A Bayesian approach to structure discovery in Bayesiannetworks[J]. Machine learning, 2003, 50(1-2): 95-125.
[62] Laskey K B, Myers J W. Population markovchain monte carlo[J]. Machine Learning, 2003, 50(1): 175-196.
[101] Madigan D, York J, Allard D. Bayesiangraphical models for discrete data[J]. International Statistical Review/RevueInternationale de Statistique, 1995: 215-232.
[102] Giudici P, Castelo R. ImprovingMarkov chain Monte Carlo model search for data mining[J]. Machine learning,2003, 50(1-2): 127-158.
从页码可以看出,这几篇文献篇幅都比较长,就不去细究了。接下来重点说说基于工具箱FullBNT-1.0.4的实现。
函数文件路径:\FullBNT-1.0.4\BNT\learning\learn_struct_mcmc.m
例子文件路径:\FullBNT-1.0.4\BNT\examples\static\StructLearn\mcmc1.m
learn_struct_mcmc.m的代码如下:
function [sampled_graphs, accept_ratio, timing] = learn_struct_mcmc(data, ns, varargin)
% MY_LEARN_STRUCT_MCMC Monte Carlo Markov Chain search over DAGs assuming fully observed data
% [sampled_graphs, accept_ratio, num_edges] = learn_struct_mcmc(data, ns, ...)
%
% data(i,m) is the value of node i in case m.
% ns(i) is the number of discrete values node i can take on.
%
% sampled_graphs{m} is the m'th sampled graph.
% accept_ratio(t) = acceptance ratio at iteration t
% num_edges(t) = number of edges in model at iteration t
%
% The following optional arguments can be specified in the form of name/value pairs:
% [default value in brackets]
%
% scoring_fn - 'bayesian' or 'bic' [ 'bayesian' ]
% Currently, only networks with all tabular nodes support Bayesian scoring.
% type - type{i} is the type of CPD to use for node i, where the type is a string
% of the form 'tabular', 'noisy_or', 'gaussian', etc. [ all cells contain 'tabular' ]
% params - params{i} contains optional arguments passed to the CPD constructor for node i,
% or [] if none. [ all cells contain {'prior', 1}, meaning use uniform Dirichlet priors ]
% discrete - the list of discrete nodes [ 1:N ]
% clamped - clamped(i,m) = 1 if node i is clamped in case m [ zeros(N, ncases) ]
% nsamples - number of samples to draw from the chain after burn-in [ 100*N ]
% burnin - number of steps to take before drawing samples [ 5*N ]
% init_dag - starting point for the search [ zeros(N,N) ]
%
% e.g., samples = my_learn_struct_mcmc(data, ns, 'nsamples', 1000);
%
% Modified by Sonia Leach (SML) 2/4/02, 9/5/03
tic
[n ncases] = size(data);
% set default params
type = cell(1,n);
params = cell(1,n);
for i=1:n
type{i} = 'tabular';
%params{i} = { 'prior', 1};
params{i} = { 'prior_type', 'dirichlet', 'dirichlet_weight', 1 };
end
scoring_fn = 'bayesian';
discrete = 1:n;
clamped = zeros(n, ncases);
nsamples = 100*n;
burnin = 5*n;
dag = zeros(n);
lML = [];
args = varargin;
nargs = length(args);
for i=1:2:nargs
switch args{i},
case 'nsamples', nsamples = args{i+1};
case 'burnin', burnin = args{i+1};
case 'init_dag', dag = args{i+1};
case 'scoring_fn', scoring_fn = args{i+1};
case 'type', type = args{i+1};
case 'discrete', discrete = args{i+1};
case 'clamped', clamped = args{i+1};
case 'lML', lML = args{i+1};
case 'params', if isempty(args{i+1}), params = cell(1,n); else params = args{i+1}; end
end
end
% We implement the fast acyclicity check described by P. Giudici and R. Castelo,
% "Improving MCMC model search for data mining", submitted to J. Machine Learning, 2001.
% SML: also keep descendant matrix C
use_giudici = 1;
if use_giudici
[nbrs, ops, nodes, A] = mk_nbrs_of_digraph(dag);
else
[nbrs, ops, nodes] = mk_nbrs_of_dag(dag);
A = [];
end
num_accepts = 1;
num_rejects = 1;
T = burnin + nsamples;
accept_ratio = zeros(1, T);
num_edges = zeros(1, T);
sampled_graphs = cell(1, nsamples);
timing = zeros(1,T-burnin);
%sampled_bitv = zeros(nsamples, n^2);
for t=1:T
[dag, nbrs, ops, nodes, A, accept] = take_step(dag, nbrs, ops, ...
nodes, ns, data, clamped, A, ...
scoring_fn, discrete, type, params, lML );
num_edges(t) = sum(dag(:));
num_accepts = num_accepts + accept;
num_rejects = num_rejects + (1-accept);
accept_ratio(t) = num_accepts/(num_rejects+num_accepts);
if t > burnin
sampled_graphs{t-burnin} = dag;
%sampled_bitv(t-burnin, :) = dag(:)';
timing(t-burnin) = toc;
end
if mod(t, 1000)==0
fprintf('%i/%i %f\n', t, T, accept_ratio(t));
end
end
%%%%%%%%%
function [new_dag, new_nbrs, new_ops, new_nodes, A, accept] = ...
take_step(dag, nbrs, ops, nodes, ns, data, clamped, A, ...
scoring_fn, discrete, type, params, lML, prior_w )
use_giudici = ~isempty(A);
if use_giudici
[new_dag, op, i, j, new_A] = pick_digraph_nbr(dag, nbrs, ops, nodes,A); % updates A
[new_nbrs, new_ops, new_nodes] = mk_nbrs_of_digraph(new_dag, new_A);
else
d = sample_discrete(normalise(ones(1, length(nbrs))));
new_dag = nbrs{d};
op = ops{d};
i = nodes(d, 1); j = nodes(d, 2);
[new_nbrs, new_ops, new_nodes] = mk_nbrs_of_dag(new_dag);
end
bf = bayes_factor(dag, new_dag, op, i, j, ns, data, clamped, scoring_fn, discrete, type, params, lML);
%R = bf * (new_prior / prior) * (length(nbrs) / length(new_nbrs));
R = bf * (length(nbrs) / length(new_nbrs));
u = rand(1,1);
if u > min(1,R) % reject the move
accept = 0;
new_dag = dag;
new_nbrs = nbrs;
new_ops = ops;
new_nodes = nodes;
else
accept = 1;
if use_giudici
A = new_A; % new_A already updated in pick_digraph_nbr
end
end
%%%%%%%%%
function bfactor = bayes_factor(old_dag, new_dag, op, i, j, ns, data, clamped, scoring_fn, discrete, type, params, lML)
if isempty(lML)
u = find(clamped(j,:)==0);
LLnew = score_family(j, parents(new_dag, j), type{j}, scoring_fn, ns, discrete, data(:,u), params{j});
LLold = score_family(j, parents(old_dag, j), type{j}, scoring_fn, ns, discrete, data(:,u), params{j});
else
paNew = find(new_dag(:,j));
paOld = find(old_dag(:,j));
kNew = sum(2.^(paNew-1));
kOld = sum(2.^(paOld-1));
LLnew = lML(j, kNew+1);
LLold = lML(j, kOld+1);
end
bf1 = exp(LLnew - LLold);
if strcmp(op, 'rev') % must also multiply in the changes to i's family
if isempty(lML)
u = find(clamped(i,:)==0);
LLnew = score_family(i, parents(new_dag, i), type{i}, scoring_fn, ns, discrete, data(:,u), params{i});
LLold = score_family(i, parents(old_dag, i), type{i}, scoring_fn, ns, discrete, data(:,u), params{i});
else
paNew = find(new_dag(:,i));
paOld = find(old_dag(:,i));
kNew = sum(2.^(paNew-1));
kOld = sum(2.^(paOld-1));
LLnew = lML(i, kNew+1);
LLold = lML(i, kOld+1);
end
bf2 = exp(LLnew - LLold);
else
bf2 = 1;
end
bfactor = bf1 * bf2;
%%%%%%%% Giudici stuff follows %%%%%%%%%%
% SML: This now updates A as it goes from digraph it choses
function [new_dag, op, i, j, new_A] = pick_digraph_nbr(dag, digraph_nbrs, ops, nodes, A)
d = sample_discrete(normalise(ones(1, length(digraph_nbrs))));
%d = myunidrnd(length(digraph_nbrs),1,1);
i = nodes(d, 1); j = nodes(d, 2);
new_dag = digraph_nbrs(:,:,d);
op = ops{d};
new_A = update_ancestor_matrix(A, op, i, j, new_dag);
%%%%%%%%%%%%%%
function A = update_ancestor_matrix(A, op, i, j, dag)
switch op
case 'add',
A = do_addition(A, op, i, j, dag);
case 'del',
A = do_removal(A, op, i, j, dag);
case 'rev',
A = do_removal(A, op, i, j, dag);
A = do_addition(A, op, j, i, dag);
end
%%%%%%%%%%%%
function A = do_addition(A, op, i, j, dag)
A(j,i) = 1; % i is an ancestor of j
anci = find(A(i,:));
if ~isempty(anci)
A(j,anci) = 1; % all of i's ancestors are added to Anc(j)
end
ancj = find(A(j,:));
descj = find(A(:,j));
if ~isempty(ancj)
for k=descj(:)'
A(k,ancj) = 1; % all of j's ancestors are added to each descendant of j
end
end
%%%%%%%%%%%
function A = do_removal(A, op, i, j, dag)
% find all the descendants of j, and put them in topological order
% SML: originally Kevin had the next line commented and the %* lines
% being used but I think this is equivalent and much less expensive
% I assume he put it there for debugging and never changed it back...?
descj = find(A(:,j));
%* R = reachability_graph(dag);
%* descj = find(R(j,:));
order = topological_sort(dag);
% SML: originally Kevin used the %* line but this was extracting the
% wrong things to sort
%* descj_topnum = order(descj);
[junk, perm] = sort(order); %SML:node i is perm(i)-TH in order
descj_topnum = perm(descj); %SML:descj(i) is descj_topnum(i)-th in order
% SML: now re-sort descj by rank in descj_topnum
[junk, perm] = sort(descj_topnum);
descj = descj(perm);
% Update j and all its descendants
A = update_row(A, j, dag);
for k = descj(:)'
A = update_row(A, k, dag);
end
%%%%%%%%%%%
function A = old_do_removal(A, op, i, j, dag)
% find all the descendants of j, and put them in topological order
% SML: originally Kevin had the next line commented and the %* lines
% being used but I think this is equivalent and much less expensive
% I assume he put it there for debugging and never changed it back...?
descj = find(A(:,j));
%* R = reachability_graph(dag);
%* descj = find(R(j,:));
order = topological_sort(dag);
descj_topnum = order(descj);
[junk, perm] = sort(descj_topnum);
descj = descj(perm);
% Update j and all its descendants
A = update_row(A, j, dag);
for k = descj(:)'
A = update_row(A, k, dag);
end
%%%%%%%%%
function A = update_row(A, j, dag)
% We compute row j of A
A(j, :) = 0;
ps = parents(dag, j);
if ~isempty(ps)
A(j, ps) = 1;
end
for k=ps(:)'
anck = find(A(k,:));
if ~isempty(anck)
A(j, anck) = 1;
end
end
%%%%%%%%
function A = init_ancestor_matrix(dag)
order = topological_sort(dag);
A = zeros(length(dag));
for j=order(:)'
A = update_row(A, j, dag);
end
mcmc1.m的代码如下:
% We compare MCMC structure learning with exhaustive enumeration of all dags.
N = 3;
%N = 4;
dag = mk_rnd_dag(N);
ns = 2*ones(1,N);
bnet = mk_bnet(dag, ns);
for i=1:N
bnet.CPD{i} = tabular_CPD(bnet, i);
end
ncases = 100;
data = zeros(N, ncases);
for m=1:ncases
data(:,m) = cell2num(sample_bnet(bnet));
end
dags = mk_all_dags(N);
score = score_dags(data, ns, dags);
post = normalise(exp(score));
[sampled_graphs, accept_ratio] = learn_struct_mcmc(data, ns, 'nsamples', 100, 'burnin', 10);
mcmc_post = mcmc_sample_to_hist(sampled_graphs, dags);
if 0
subplot(2,1,1)
bar(post)
subplot(2,1,2)
bar(mcmc_post)
print(gcf, '-djpeg', '/home/cs/murphyk/public_html/Bayes/Figures/mcmc_post.jpg')
clf
plot(accept_ratio)
print(gcf, '-djpeg', '/home/cs/murphyk/public_html/Bayes/Figures/mcmc_accept.jpg')
end
首先来说函数learn_struct_mcmc.m,此函数必须设置的输入参数比较少,大部分可以默认。仅两个必须的输入参数如下:
data和ns,含义与learn_struct_K2.m相同(参见《贝叶斯网络结构学习之K2算法(基于FullBNT-1.0.4的MATLAB实现)》)
% data(i,m) is the value of node i in case m.
% ns(i) is the number of discrete values node i can take on.
再解释nsamples和burnin两个可选输入参数,因为例子当中用到了这两个参数:
因为MCMC本身就是通过多次迭代收敛到平稳状态,此时产出的样本近似服从分布p。也就是说必须经过多次迭代后产生的样本才是符合要求的,因此需要设定两个参数。第一个是从第几次迭代之后开始产生的样本认为符合要求,此即burnin参数;第二个是一共产生多少个合格的样本(诚然贝叶斯网络结构只需每次产生一个即可,但很多MCMC应用实际上是产生多个样本求期望),此即nsamples参数;因此总共迭代次数是nsamples+burnin,即前burnin次迭代产生的结果舍掉,保存后nsamples次迭代结果。
% nsamples - number of samples to draw from the chain after burn-in [ 100*N ]
% burnin - number of steps to take before drawing samples [ 5*N ]
以上注释中最后中括号内的值为此参数的默认值。其它参数含义详见函数注释。
值得注意的是,learn_struct_mcmc.m的第66~67行提到了一篇参考文献,个人认为应该是上面提到的四篇英文文献的最后一篇,即【Giudici P, Castelo R. Improving Markov chain Monte Carlo modelsearch for data mining[J]. Machine learning, 2003, 50(1-2): 127-158.】。
接下来说例子mcmc1.m,此例子的大致流程是:
(1)人工生成一个贝叶斯网络BN(含结构和参数)(前10行);
(2)根据贝叶斯网络BN生成数据集D(第12~16行);
(3)得到所有结点个数为N的贝叶斯网络结构并用评分函数进行依次评分(第18~20行);
(4)调用learn_struct_mcmc函数根据数据集D学习网络结构(第22行);
(5)对学得的所有网络结构进行统计,得到每种网络结构的比例(第23行)
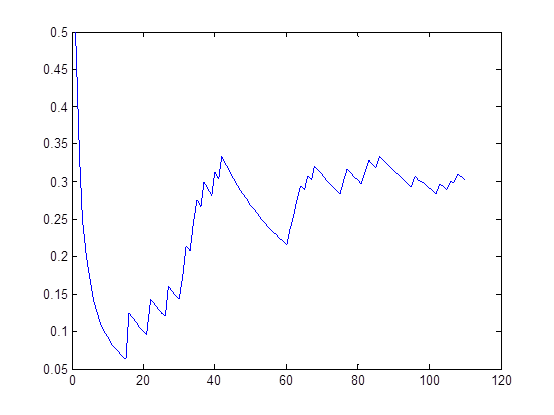
(6)画出第3步所有评分函数的柱状图和第5步学得各种网络结构比例的柱状图(第26~29行),以及接受概率曲线图(第33行)。
直接运行mcmc1.m,贴三张图,结合这三张图进一步解释整个例子细节:
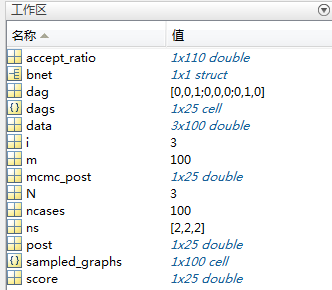
图1 工作区变量
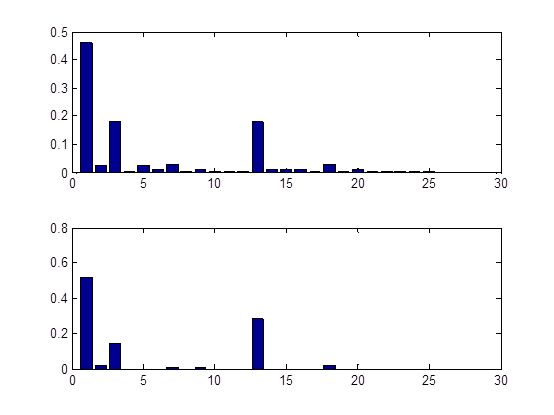
图3 接受概率曲线图
前两步没什么特别的,生成一个人工数据集供后面使用。
第3步先是得到所有结点个数为N的贝叶斯网络结构(第18行),从图1可以知道dags大小为25,也就是说共有25种合法的网络结构(有向无环图);此处节点个数N=3,任意两个节点A和B之间可以由A指向B,也可以由B指向A,也可以没有连接,因此共三种情况,而三个节点共有三对节点,因此共计3^3=27种可能的结构,但这里面有两种结构并不是有向无环图,如下图所示:

图4 两种非有向无环图
因此共计27-2=25种结构。得到所有结构之后,对每种结构用评分函数进行打分(第19行),可以执行“edit score_dags”命令打开score_dags.m文件看一下,其实就是调用评分函数score_family依次计算每种结构的评分,每种网络结构的评分是该结构中各节点评分之和。接下来,第20行对评分结果求指数并正规化(即所有评分结果之和为1),但是为什么要调用exp求指数我并不是很明白,第19行得到的score都是负数,用exp转换后就变为0和1之间的数,不知道是不是这个原因。
第4步调用learn_struct_mcmc函数,输入参数当中data即为前两部生成的数据集,ns为各个节点可能的取值个数(每个节点的取值是离散的,只有有限的几个值);接下来nsamples设置为100即得到100个采样结果(贝叶斯网络结构),burnin设置为10意思是舍弃最初的10次采样结果(贝叶斯网络结构)。输出参数有两个,sampled_graph存储着100个采样结果,accept_ratio存储着历史采样的接受概率。从图1中可以知道sampled_graphs大小为100,即采样个数,accept_ratio大小为110,即所有采样次数nsamples+burnin。
这里有一个最关键问题:我只是想调用learn_struct_mcmc函数根据数据集data学得一个最好的贝叶斯网络结果,但这个函数却输出了很多个(例子中sampled_graphs存储着100种结构,因为最多才25种结构,即100个结果肯定有相互一样的),到底选哪一个呢?是不是最后一次采样结果就是最好的结构呢?因为迭代次数越多结果应该越稳定呀。这应该是每一个使用者疑问,毕竟作为一个普通人,仅想调用某个结构学习函数根据数据集学到一个贝叶斯网络结构而已。答案很简单,选择在结果中出现次数最多的那一个结构!
第5步调用mcmc_sample_to_hist函数,对学得的所有网络结构进行统计,得到每种网络结构的比例。比如例子中共有25可能的结构,mcmc_sample_to_hist将sampled_graphs中的100种结构与25种可能的结构进行对比,统计每一种可能结构在sampled_graphs中的出现次数,再正规化,即分别计算出25种可能的结构在100个采样结果中出现的比例。
第6步是绘出显示工作,执行与否由第25行的if语句决定,默认不执行,若要执行则将if 0改为if 1即可。第27行将可能的25种结构的正规化评分结果(第20行所得)用柱状图显示,第29行将sampled_graphs正规化的统计结果(第23行所得)用柱状图显示,分别如图2的上图和下图所示。第33行绘出每次迭代的接受概率,因为Metropolis-Hastings算基于“拒绝采样”(reject sampling)来逼近平稳分布的。
比较图2中的两幅子图可以发现,它们很相识!是的,MCMC方法的关键就在于通过构造“平稳分布为p的马尔可夫链”来产生样本:若马尔可夫链运行时间足够长(即收敛到平稳状态),则此时产出的样本x近似服从于分布p(摘自西瓜书P333)。learn_struct_mcmc函数产生的样本x即为sampled_graphs中的网络结构,分布p即为第20行得到的正规化的各种结构评分结果。到此,应该明白选择sampled_graphs中的哪一个结构了吧,出现频率服从正规化评分结果,即出现次数越多的结构评分越好;因此,当然选择sampled_graphs中出现次数最多的那一个结构!
可能你会发现,第5行生成的dag并不是评分最好的结构。也就是说基于结构dag生成数据集D,但在此数据集D上用评分函数去评价各种可能的结构时有优于dag的结构!打个比方说,你(结构dag)生的孩子(数据集D)长的居然不是与你长的最像?!为什么呢?不是亲生的?稍安勿躁,孩子还是亲生的^_^,只是决定孩子长像的除了你(结构dag)之外还有你的另一半(网络参数),另外遗传过程除了crossover还有mutation,所以淡定淡定^_^
总结一下这个例子,首先人工生成数据集,然后对比MCMC结构学习结果正规化分布与所有可能结构的评分正规化分布。其实例子第1行的注释已经说明了:
% We compare MCMC structure learning withexhaustive enumeration of all dags.另外,特别注意一下learn_struct_mcmc函数的输入参数nsamples和burnin的设置,本例中分别设置为100和10,默认值分别是100*N和5*N(N为节点个数,本例中N=3),当在实际中应用该函数时节点个数一般大于3,所以就不要再使用本例中的100和10两个值了,其实最简单的办法就是不管这两个参数,直接使用默认值!
下面是我对learn_struct_mcmc进行了二次封装处理所得的learn_struct_mcmc_basic.m,输入参数只有数据集data,输出是评分结果最好的网络结构:
function [DAG] = learn_struct_mcmc_basic(data)
%调用工具箱FullBNT-1.0.4中的learn_struct_mcmc函数学习贝叶斯网络结构
%该函数主要是对learn_struct_mcmc进行二次封装
%输入仅有data,输出即为学得贝叶斯网络结构DAG
%节点个数
N = size(data,1);
%得到learn_struct_mcmc的输入参数ns
ns = zeros(1,N);
for nn=1:N
ns_temp = unique(data(nn,:));
ns(1,nn)=length(ns_temp);
end
%调用learn_struct_mcmc
[sampled_graphs, ~] = learn_struct_mcmc(data, ns);
%将sampled_graphs的所有结构矩阵展成一行存在sampled_bitvs
nsamples = length(sampled_graphs);%结构个数
sampled_bitvs = zeros(nsamples, N*N);
for nn=1:nsamples
sampled_bitvs(nn, :) = sampled_graphs{nn}(:)';
end
%找出sampled_graphs中共有多少种不同的结果(即去除重复的结构)
[ugraphs, I, J] = unique(sampled_bitvs, 'rows');
%统计每种结构的个数
num = zeros(1,length(I));
for nn=1:length(I)
num(nn) = sum(J==nn);
end
%根据统计结果找出出现次数最多的结构
[~,p] = max(num);
DAG = reshape(ugraphs(p,:),N,N);%恢得N*N矩阵
%DAG= reshape(sampled_bitvs(I(p),:),N,N)
end但是,我多次运行learn_struct_mcmc函数,发现对于同一数据集,每次的结果都是不同的,这也很正常,因为本身该函数使用了Metropolis-Hastings算法,里面的有一定的随机性。
最后总结一下基于MCMC的结构学习方法本质:该方法不同于K2算法直接搜索评分函数值最大的结构,而是通过构建一个马尔可夫链,使其收敛至平稳分布p(该分布即为每种贝叶斯网络结构的规格化评分函数值,即例子中的第20行得到的结果,该分布在真实应用中是未知的,因为当贝叶斯网络节点个数较多时不可能遍历每种结构求出其评分函数值,但通过MCMC方法却可以近似产生分布服从p的样本),依此马尔可夫链产生的样本(即网络结构)中出现次数最多(出现概率最大)的结构即为评分函数最好的结构。因此基于MCMC的结构学习方法本质上讲仍然是基于评分搜索的方法,只是这种搜索策略并不是直接搜索评分函数最优的网络结构,而是按各种结构的评分函数值大小为概率产生好多结构。所以一般文献也会将此方法归类到基于评分搜索的方法之中,例如:
【胡春玲. 贝叶斯网络结构学习及其应用研究[D]. 合肥工业大学, 2011.】

只是不清楚为何上图文献的作者在3.3.1节如此描述完之后(注意上图最后四个字“抽样算法”)又在3.3.3节单列一节专门讲述“基于随机抽样的贝叶斯网络结构学习”,可能正如3.3.3节第一段最后一句话所述,“将随机抽样的思想引入评分搜索学习方法的搜索过程是解决评分搜索算法收敛于局部最优的有效途径之一”,作者虽然在3.3.1节点明确了抽样算法是一种搜索策略,但可能又发现基于随机抽样的思想不同于普通的搜索策略,所以单列说明。

另外,从这个算法中可以进一步理解何为蒙特卡罗(Monte Carlo)仿真,蒙特卡罗仿真的确是通过大量仿真来说明问题的,但绝不是随机进行仿真的,而是按实际概率分布进行抽样得到样本后进行大量仿真分析。再回到MCMC方法,就是先通过构造马尔可夫链得到分布为p的样本(这是蒙特卡罗仿真的前提),然后再进行蒙特卡罗分析。
附录1:西瓜书中有关MCMC方法(MH算法和Gibbs采样)
由于MCMC是一种采样技术,所以首先说明为什么要研究采样技术:


介绍完了为什么要用采样法,开始转入MCMC方法,“概率图模型中最常用的采样技术是MCMC方法”,对MCMC简单介绍之后又转入一种MCMC具体算法——MH算法:

接受概率为什么等于式(14.28)呢?把式(14.28)代入式(14.27)立马就明白了,具体可参见英文书PRML中的式(11.45),附录2中也会有截图。
Gibbs采样在西瓜书中是在贝叶斯网络推断中讲述的:

这只是Gibbs采样在贝叶斯网络近似推断中的具体应用,更通用的表达参见PRML。
附录2:PRML中有关MCMC方法(MH算法和Gibbs采样)
PRML中并没有一个单独的MCMC方法或具体的MH算法的步骤,从11.2.2节开始讨论MH算法,给出了接受概率表达式(11.44):

其中文中提到的式(11.33)如下:

文中提到的式(11.40)如下:

为什么接收概率如此设置呢?证明如下:

有关Gibbs采样在PRML中有一个通用的描述:
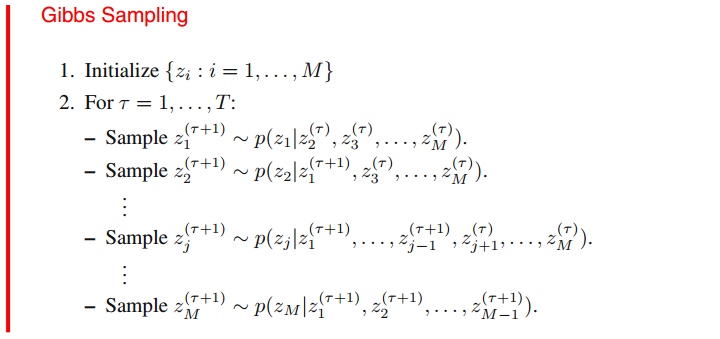
为什么说Gibbs采样可以看成是MH算法的一个特例呢?

即Gibbs采样相当于MH算法接收概率等于1的特殊情形。