1、消元知识点脑图
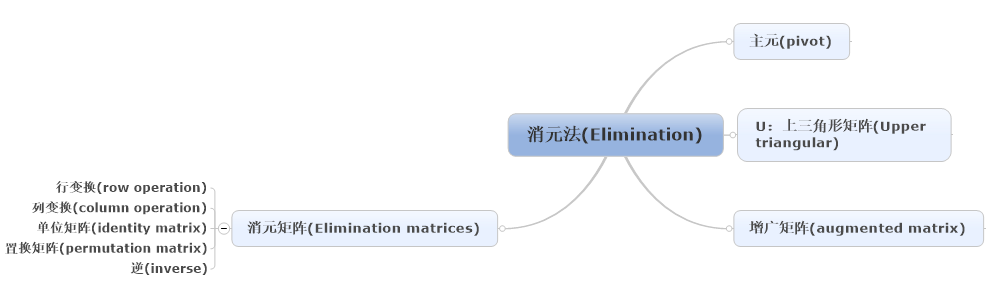
2、消元法
消元是求解方程组的过程。初中时期我们学习过通过方程之间的加减操作,消除某个变量的系数,简化方程,最终求出变量值。在线性代数里,将消元进一步系统化,因此引入了几个概念。我们以一组方程为例。
\[ \begin{cases} & \text x+ 2y + z = 2 & (1)\\ & \text 3x+8y+z=12 & (2)\\ & \text 4y+z=2 & (3) \end{cases} \]
我们用矩阵形式来表示该方程组。
\[ \begin{bmatrix} 1&2 &1 \\ 3&8 &1 \\ 0&4 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 2\\ 12\\ 2 \end{bmatrix} \]
简化后是
\[ AX=b \]
(1)组成增广矩阵
\[ \begin{bmatrix} 1&2 &1 &2\\ 3&8 &1 &12\\ 0&4 &1 &2 \end{bmatrix} \]
增广矩阵是系数矩阵A与b向量合并后的矩阵,下面我们通过这个增广矩阵来进行消元,使得方程左右两边同时变化。大家不理解的时候可以想想方程组的变化。
(2)消元(2,1)元素
这步消元是消除方程2的x变量。
\[ \begin{bmatrix} \underline{1}&2 &1 &2 \\ 3&8 &1 &12\\ 0&4 &1 &2 \end{bmatrix} \overset{(2,1)}{\rightarrow} \begin{bmatrix} 1&2&1 &2\\ 0&2&-2 &6\\ 0&4&1 & 2 \end{bmatrix} \]
首先选择(1,1)元素作为主元(图中画下划线),消元(2,1)元素。执行如下操作:
\[ Row2 = Row2 + Row1\times (-3) \]
(3)消元(3,1)元素
这一步是消除方程3的(3,1)元素,因为方程3的(3,1)元素为0所以不用继续,若不为0,可以参照步骤2。
(4)消元(3,2)元素
下面进一步消除第三行y的系数。先确定主元(2,2),大家可以思考下如果(2,2)是0如何操作?
\[ \begin{bmatrix} 1&2&1 &2\\ 0&{\underline{2}}&-2 &6\\ 0&4&1&2 \end{bmatrix} \]
执行消除(3,2)
\[ Row3 = Row3 + Row2\times(-2) \]
变化如下:
\[ \begin{bmatrix} 1&2&1 &2\\ 0&{\underline{2}}&-2 &6\\ 0&4&1 &2 \end{bmatrix}\overset{(3,2)}{\rightarrow} \begin{bmatrix} 1&2&1 &2\\ 0&2&-2 &6\\ 0&0&5&-10 \end{bmatrix} \]
(5)回代
经过上面步骤消元后的矩阵等式变成:
\[ \begin{bmatrix} 1&2&1 \\ 0&2&-2 \\ 0&0&5 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix}= \begin{bmatrix} 2\\ 6\\ -10 \end{bmatrix} \]
这里的系数矩阵左下角都是0,称为上三角矩阵(Upper triangular)简称U。
先求出z,代入第二行求出y,最后代入第一行求出x。
\[ \begin{cases} & x=2 \\ & y=1 \\ &z=-2 \end{cases} \]
主元:是指在消元过程中起主导作用的元素。
3、消元矩阵
上面的步骤我们还是按照传统求解方程组的形式进行消元,现在我们切换到矩阵形式,以矩阵的语言来表示上面的消元矩阵。
参考第一节的方式简化消元后的矩阵。
令
\[ U=\begin{bmatrix} 1&2&1 \\ 0&2&-2 \\ 0&0&5 \end{bmatrix} \]
\[ c=\begin{bmatrix} 2 \\ 6 \\ -10 \end{bmatrix} \]
矩阵方程可以简化为
\[ UX=c \]
那这样只要将A与某个矩阵相乘得到U,就能算出整个方程组的解了:
\[ ?A=U \]
按照上面的消元步骤,分两步变化:
\[ E_{32}(E_{21}A)=U \]
这里的E称为初等矩阵,乘法的结合律在这里依然适用(交换律不适用)于是整个式子就变成了:
\[ (E_{32}E_{21})A=U \]
这里要首先介绍下矩阵变换
令
\[ A=\begin{bmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{bmatrix} \\ B=\begin{bmatrix} b_{11}&b_{12}&b_{13} \\ b_{21}&b_{22}&b_{23} \\ b_{31}&b_{32}&b_{33} \end{bmatrix} \\ x = \begin{bmatrix} x_{11} \\ x_{21} \\ x_{31} \end{bmatrix} \\ y = \begin{bmatrix} y_{11} & y_{12} &y_{13} \end{bmatrix} \]
(1)列变换
\[ Ax= x_{11}Col1 + x_{21}Col2 + x_{31}Col3 \]
矩阵右乘向量就是A的列向量的线性组合。
(2)行变换
\[ yA= y_{11}Row1 + y_{12}Row2 + y_{13}Row3 \]
矩阵左乘向量就是A的行向量的线性组合。
(3)矩阵相乘
\[\small{C=AB \\ = \begin{bmatrix} c_{11}=a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}&c_{12}=a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}&c_{13}=a_{11}b_{13}+a_{12}b_{23}+a_{13}b_{33} \\ c_{21}=a_{21}b_{11}+a_{22}b_{21}+a_{23}b_{31}&c_{22}=a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32}&c_{23}=a_{21}b_{13}+a_{22}b_{23}+a_{23}b_{33} \\ c_{31}=a_{31}b_{11}+a_{32}b_{21}+a_{33}b_{31}&c_{32}=a_{31}b_{12}+a_{32}b_{22}+a_{33}b_{32}&c_{33}=a_{31}b_{13}+a_{32}b_{23}+a_{33}b_{33} \end {bmatrix} (1)\\ =\begin{bmatrix} col1=A\begin{bmatrix} b_{11} \\ b_{21} \\ b_{31} \end{bmatrix}& col2=A\begin{bmatrix} b_{12}\\b_{22}\\b_{32} \end{bmatrix} & col3=A\begin{bmatrix} b_{13}\\b_{23}\\b_{33} \end{bmatrix} \end {bmatrix} (2) \\ = \begin{bmatrix} row1=\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix}B \\ row2=\begin{bmatrix} a_{21} & a_{22} & a_{23} \end{bmatrix}B \\ row3=\begin{bmatrix} a_{31} & a_{32} & a_{33} \end{bmatrix}B \end {bmatrix} (3)} \]
可以看出A决定了C的行,B决定了C的列。从行的角度理解,C的每行就是B各行按照A对应行向量的线性组合;从列的角度理解,C的各列就是A各列按照B对应列向量的线性组合。
(4)计算E
根据上面提供的矩阵相乘(第二种)的思路。首先计算出
\[ E_{21}=\begin {bmatrix} 1&0&0 \\ -3&1&0 \\ 0&0&1 \end {bmatrix} \\ E_{32}=\begin {bmatrix} 1&0&0\\ 0&1&0\\ 0&-2&1 \end {bmatrix} \\ E = E_{32}E_{21} = \begin {bmatrix} 1&0&0\\ -3&1&0\\ 6&-2&1 \end {bmatrix} \]
大家可以代入式中计算下
\[ EA=U \]
是否成立。
4、逆
上面的E我们是依靠消元的步骤求出,并不是完全采用矩阵的形式。数学家们使用了另一种办法。
\[ EA=U \\ 只需 E^{-1}EA=E^{-1}U => A=E^{-1}U \]
也就是先求E的逆矩阵,再求E。关于逆会在后续介绍。
5、矩阵置换
有一类特殊矩阵,可以交换矩阵的行或列。这类矩阵就是置换矩阵。例如
\[I= \begin {bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end {bmatrix} \]
对角线为1,其余为0的矩阵为单位矩阵,任何矩阵有AI=IA=A。而将单位矩阵某些行或列交换形成的矩阵称为置换矩阵记为P。
(1)行交换
交换1,2行
\[ PA= \begin {bmatrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end {bmatrix} \begin {bmatrix} a&b&c\\ d&e&f\\ g&h&i \end {bmatrix}=\begin {bmatrix} d&e&f\\ a&b&c\\ g&h&i \end {bmatrix} \]
要交换行,只需先交换I的指定行,然后左乘矩阵。
(2)列交换
交换1,2列
\[ AP= \begin {bmatrix} a&b&c\\ d&e&f\\ g&h&i \end {bmatrix} \begin {bmatrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end {bmatrix} = \begin {bmatrix} b&a&c\\ e&d&f\\ h&g&i \end {bmatrix} \]
要交换列,只需先交换I的指定列,然后左乘矩阵。