回顾：二叉搜索树的定义与操作

二叉搜索树是指一颗空树或具有下列性质的树：

任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点

——from<维基百科>

二叉搜索树的操作包括：

查找，插入，删除；
查找小于X的元素个数/查找第k大的元素

treap的定义

treap(树堆)是一种随机二叉搜索树，相较于AVL树和红黑树等大部分二叉搜索树更加便于实现。树堆的结构并不由元素的添加顺序决定，而是随机的。因此，无论元素以何种方式添加到树堆，其树高的期望值总是一定的。

为了使树高的期望值总是一定的，每当树添加新值时，就会给此节点附加优先级(priority)。这种优先级与元素的大小和输入顺序无关，只通过随机数确定。treap总是会形成父节点的优先级高于子节点的二叉搜索树的形式。

由此可以得到treap的定义：

树堆是一种随机的二叉搜索树，但是和二叉搜索树有相同的性质
树堆的结构不由元素的添加顺序决定，而是随机的
添加新节点时，给这个节点附加优先级(priority)。这种优先结构与元素大小关系和输入顺序无关，值通过随机数确定。
树堆的条件：
- 二叉搜索树的条件：对所有节点而言，左侧子树的节点元素值小于根节点元素值，右侧子树的节点元素值大于根节点
- 堆的条件：所有节点的优先级都大于等于自身子节点的优先级

treap举例：

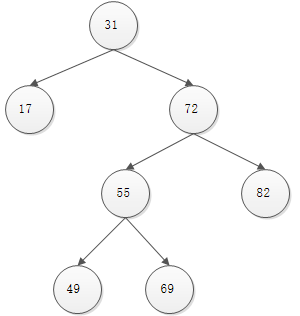
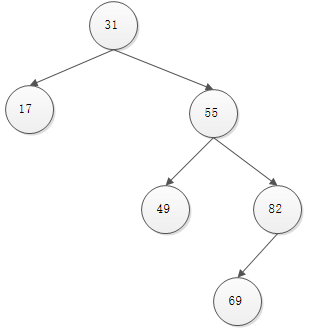
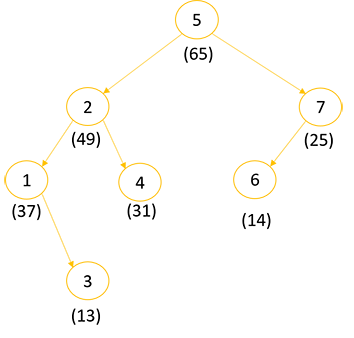
依序将1到7的整数插入到树结构中，并假设添加了随机生成的优先级，结果得到{37, 49, 13, 31, 65, 14, 25}。然后按照优先级从上到下重新排列节点得到第二张图。虽然保存元素相同，但在搜索第二张图中搜索时，因为树高更小，显然搜索地更快。

这里写图片描述
按顺序添加没有优先级限制

这里写图片描述
添加优先级，并按照优先级大小从上到下排列各节点

treap的实现

treap的实现主要有3个步骤，如下：

step1：定义结构体/对象

typedef int keyType;
//保存树堆节点
struct node{
    //保存节点的元素
    keyType key;
    //当前节点的优先级(priority)
    //将当前节点作为根节点的子树的大小(size)
    int priority, size;
    //两个子节点的指针
    node *left, *right;
    //生成器生成随机数后，初始化size和left/right指针
    node(const keyType &_key)
        : key(_key), priority(rand()), size(1), left(NULL), right(NULL){}

    void setLeft(node *newleft){left = newleft; calcSize();}
    void setRight(node *newRight){right = newRight; calcSize();}

    //更新size成员
    void calcSize()
    {
        size = 1;
        if(left) size += left->size;
        if(right) size += right->size;
    }
};

代码中首先需要注意查看树堆节点中的对象，它不仅拥有元素key，还拥有优先级priority。生成节点时，利用rand()函数返回赋值，还需要关注将自己用作子树的根，并保存子树节点个数的size()成员函数。此数值在每次left或right变更时自动更新，利用它就能够很容易地实现查找第k个元素或计算小于X的元素个数的运算。

step2：节点的添加和“分割”运算

向树堆中添加新节点的算法，主要在于保证其为二叉搜索树的条件下，还添加了优先级的相关制约条件。

扫描二维码关注公众号，回复： 3353648 查看本文章

假设现在向以root为根节点的树堆添加新节点node，先判断优先级

root更高，node添加至下一级，递归调用即可；
如果node优先级高于root，将node的元素值用作标准值，“分割”原来的树结构即split(root, key)函数，该函数将以root为根的子树分割成元素值小于key和大于key的节点。此时再用node替换掉原来的root，成为此树的新根，而split()得到的一对节点将成为node 的后代节点。

首先给出添加新节点的insert()函数，这里假设split()函数已经有定义，返回的是pair类型，first存储小于key的子树的根节点指针，second存储大于key的子树的根节点：

//向以root为根的树堆添加新节点node后，
//返回添加完毕后的新树堆的根
node* insert(node *root, node *po)
{
    if(root == NULL) return po;
    //需要用node替换根节点，将该子树一分为二
    //分别充当左右侧后代节点。
    if(root->priority < po->priority)
    {
        nodePair splitted = split(root, po->key);
        po->setLeft(splitted.first);
        po->setRight(splitted.second);
        return po;
    }
    else if(root->key < po->key)
        root->setRight(insert(root->right, po));
    else
        root->setLeft(insert(root->left, po));
    return root;
}

insert()函数向以root为根的子树添加node后返回新树的根，因为向子树添加新节点后，其根节点可能不同于原根节点。为此每次调用insert()时都会电泳setLeft()或setRight().

理解了insert的过程，下来再展示split的代码块：

typedef pair<node*, node*> nodePair;
//将以root为根的树堆分割成为所有元素值小于key的树堆
//以及大于key的树堆
nodePair split(node *root, keyType key)
{
    if(root == NULL) return nodePair(NULL, NULL);
    //如果更节点的元素值小于key，则分割右子树
    if(root->key < key)
    {
        nodePair rs = split(root->right, key);
        root->setRight(rs.first);
        return nodePair(root, rs.second);
    }
    //如果根节点的元素大于key，则分割左子树
    nodePair ls = split(root->left, key);
    root->setLeft(ls.second);
    return nodePair(ls.first, root);
}

如果有指向树堆根节点的指针root，就可以利用下列代码添加新值value:

root = insert(root, new node(value));

step3: 节点的删除和“合并”运算

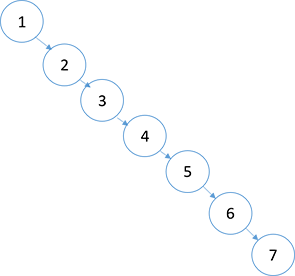
首先来介绍一下一般二叉搜索树的删除节点操作——“合并”。如果想要删除节点t，需要首先生成合并t的两个子树的树结构，然后利用此树结构替换将t用作根节点的子树。如下图所示：
删除前

删除前的二叉树如上，假设现在要删除值为72的节点，那么要将其子树合并，然后代替72成为31的右孩子。删除后的二叉树如下：

这里写图片描述

假设合并树结构A和B时，A的最大元素小于B的最小元素。A和B是节点t的左右子树，所以这种性质总是成立。那么可以将A的根节点a用作合并后的树的根节点以合并两个子树。此时，a的左侧子树中的元素都将小于a中的元素值，而右侧子树的元素和B的所有元素都大于a中元素值。因此，以递归方式合并右侧子树和B中所有元素后，将合并后的树结构用作a的右侧子节点即可。

由以上过程可知，删除节点的操作至少需要删除erase()和合并merge()两个函数的操作。

树堆节点的删除和上面所述类似，只不过合并两个子树时，将通过优先级决定哪个子树的根节点将成为树堆的根节点。

首先给出在树堆中merge()合并函数的代码，其返回a和b两颗子树合并后得到的根节点：

//a 和 b 是两个树堆，max(a) < min(b)时合并
node* merge(node *a, node *b)
{
    if(a == NULL) return b;
    if(b == NULL) return a;
    if(a->priority < b->priority)
    {
        b->setLeft(merge(a, b->left));
        return b;
    }
    a->setRight(merge(a->right, b));
    return a;
}

正如注释上所说，只有子树a中的最大元素小于子树b中的最小元素时才能合并，否则合并过程就会乱序。

下面是树堆中删除erase()操作的代码：

//以root为根的树堆中，删除key后返回树堆的根
node* erase(node *root, keyType key)
{
    if(root == NULL) return root;
    //删除root后合并两个子树并返回
    if(root->key == key)
    {
        node *ret = merge(root->left, root->right);
        delete root;
        return ret;
    }
    if(key < root->key)
        root->setLeft(erase(root->left, key));
    else
        root->setRight(erase(root->right, key));
    return root;
}

treap的操作

我们前面提到了treap的操作除了插入，删除，查找以外，还有求小于x的元素个数，按照大小顺序排序时查找第k个元素。利用二叉搜索树可以很容易实现这些运算。

但是大部分程序设计语言的标准库并不支持这些操作，所以就需要快速编写treap来实现，node类保存了其子树的大小size，所以实现这种操作并不难。

treap操作之一：查找第k个元素

以root为根的子树由左子树，右子树，root本身组成。只要知道各子树的大小，就能知道第k个节点在哪里。

这里假设左侧子树的大小为 L 时，可以分为如下三种情况考虑：

k ≤ L ：第k个节点属于左侧子树；
k = L + 1：根节点是第k个节点；
k > L + 1 : 右侧子树的第k - (L + 1)个接待你是第k个节点。

如下所示代码是算出第k个元素的kth()函数的源代码。kth()并没有特意考虑需要处理的树结构是树堆，所以此函数不仅适用于树堆，而且适用于能够得出各子树大小的二叉搜索树。

//返回 以root为根的树中第k个元素
node* kth(node *root, int k)
{
    int leftSize = 0;
    if(root->left != NULL)
        leftSize = root->left->size;
    if(k <= leftSize) return kth(root->left, k);
    if(k == leftSize + 1) return root;
    return kth(root->right, k - leftSize - 1);
}

kth()函数的时间复杂度和树高成正比。

treap操作之二：计算小于x的元素个数

搜索二叉树另一个操作是给出特定范围[a, b)时，算出此范围内所有元素个数。显然编写能够计算并返回小于x的元素个数的countLessThan(x)函数就能轻松实现此操作，因为[a, b)范围内元素个数可以用countLessThan(b) - countLessThan(a)算出。

而countLessThan(x)函数就是对查找函数的简单变形。首先判断root中的元素是否大于等于x：

如果是，则root和右侧子树中的元素全都大于x，递归左子树即可；
如果root中的元素小于x，则左侧元素都小于x。因此，左侧子树中的所有元素都要算入答案。而在右侧子树中，利用递归方式算出小于x的元素个数。最终将左右侧小于x的元素个数与根节点个数相加就能得到答案。

下面是countLessThan(x)函数的源代码，此代码也同样并不只是用于树堆，只要是节点中存储了子树大小的二叉搜索树，都能正确运行此函数。

//返回小于key的元素个数的源代码
int countLessThan(node *root, keyType key)
{
    if(root == NULL) return 0;
    if(root->key >= key)
        return countLessThan(root->left, key);
    int ls = (root->left ? root->left->size : 0);
    return ls + 1 + countLessThan(root->right, key);
}

总结与例题

以上两种实现查找第k小的元素、小于key的元素个数的操作的二叉搜索树的结构又被称为名次树(rank tree)。下面给出一道例题：
https://algospot.com/judge/problem/read/INSERTION (可能需要翻墙)
下面给出这道题的翻译：
翻转插入排序
此题的思路如下：

只要知道最后一个数值A[N-1]向左移动了几次，就能猜出A[N-1]中的数值。
例如{0,1,1,2,3}，最后一个数值A[4]向左移动3次，说明1~5的数值中，比A[4]大的数值有3个，由此得知A[4] = 2。已知2是A[4]中的数值，所以A[3]中的数值只能是1,3,4,5之一。这些数中，比A[3]大的数值有两个，可知A[3] = 3
按这种方法设计算法，需考虑能放入A[i]的各个数值如何保存。为实现此算法，必须迅速在候选集合中找出第k个元素并删除。利用二叉搜索树在O(logN)的时间内完成

具体代码就不在这里给出，如果要进一步了解此题的代码，可参考

具宗万《算法问题实战策略》22.8 解题：翻转插入排序

treap的题目还有2010天津区域赛题目Graph and Queries，这里同样给出链接
https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=393&page=show_problem&problem=3032

其实现解法与如何使用treap可参考

《算法竞赛入门经典训练指南》3.5.2节例题20

treap(树堆)

回顾： 二叉搜索树的定义与操作