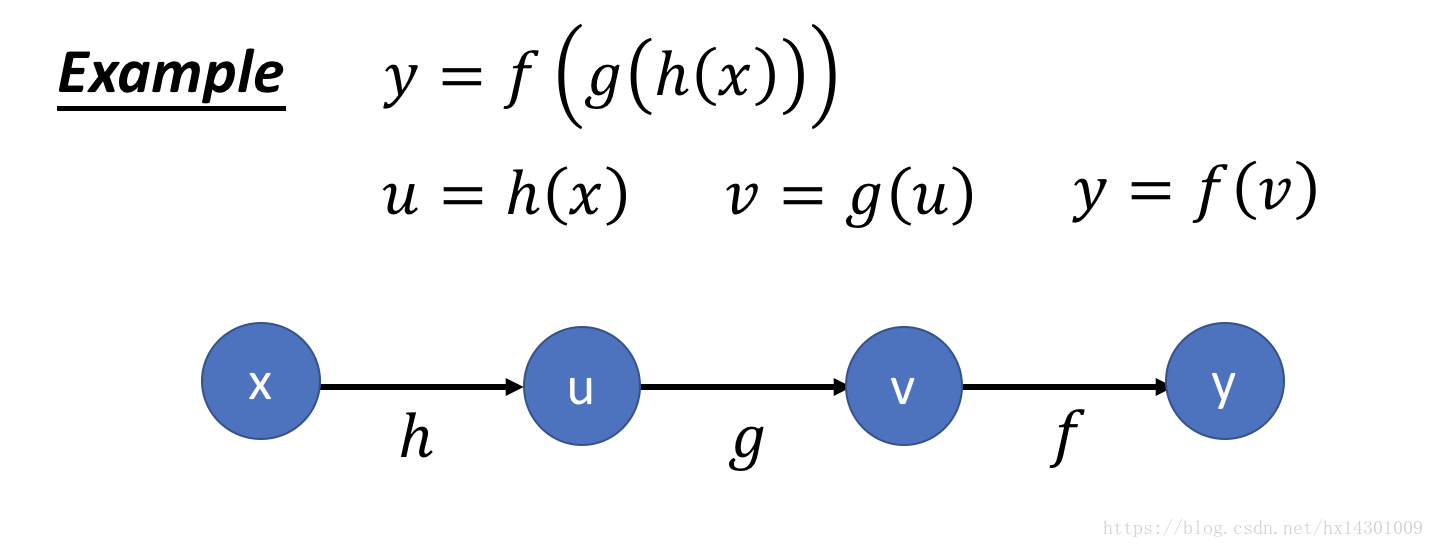最近看一些复杂网络的BP推导看的头疼,通过computational graph之后看起来会舒服很多,这里记录下:
1.准备工作
首先从最简单的图开始:
可以看到,节点表示数,可以是vector,tensor,scala等 ,连边表示一个函数操作,比如+ - * / 等等
下面画一个稍微多一点的小学计算题的计算图:
有了这个图了,我们要怎么进行BP计算梯度呢?
首先,通过正向传播,将各个节点的值计算出来,如上面那个图所示,
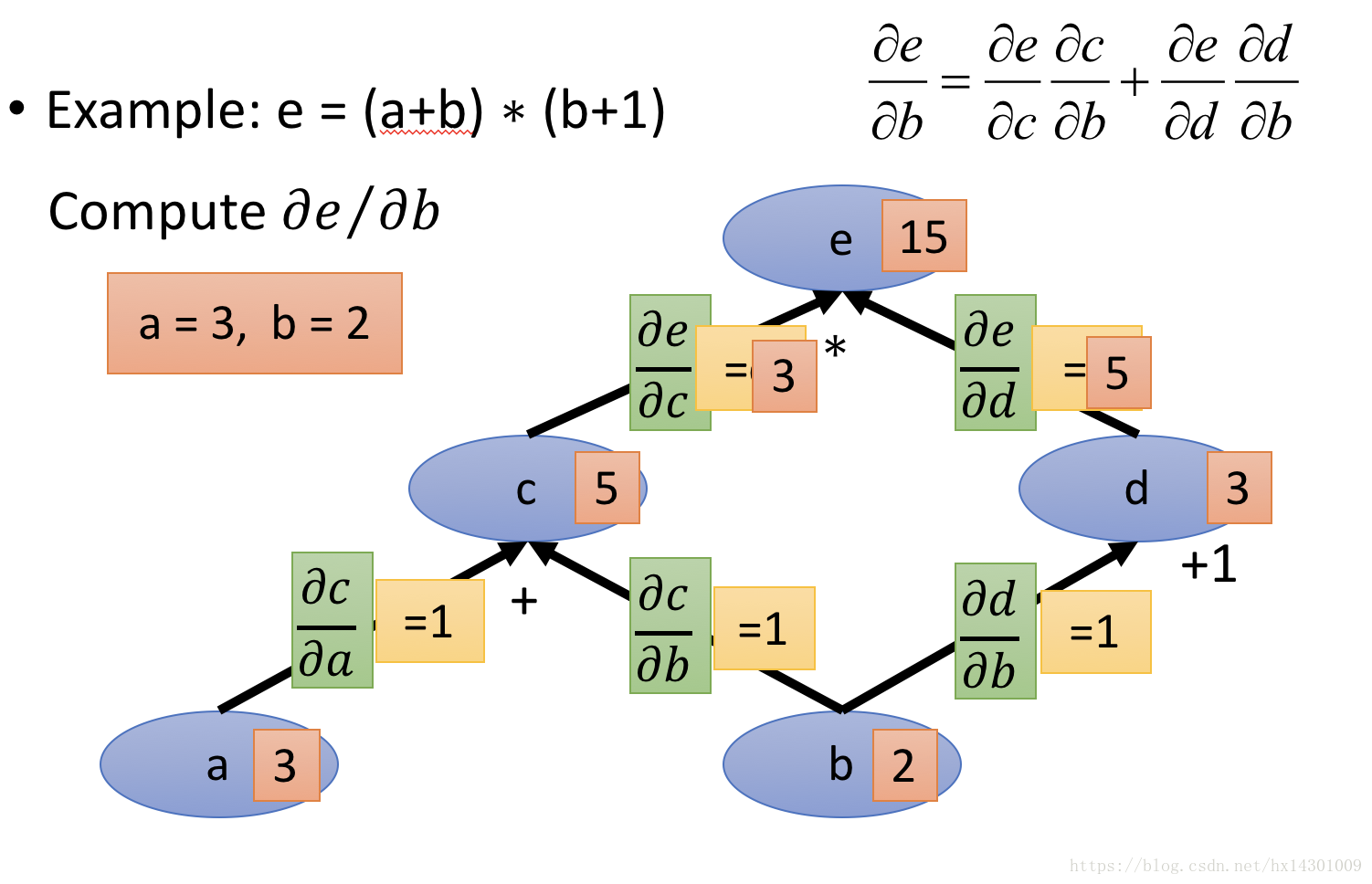
接着,我们根据各个节点的值将每条边对应的偏导求出来,如下图:
这样,我要想计算偏e/偏b,我只需要从终点e开始,沿着到b的路径,将各个边的偏导乘起来,如果遇到分支合并,比如上面的c,d一起合并到b,那么就将两条路的偏导都加起来就是对b偏导的结果。
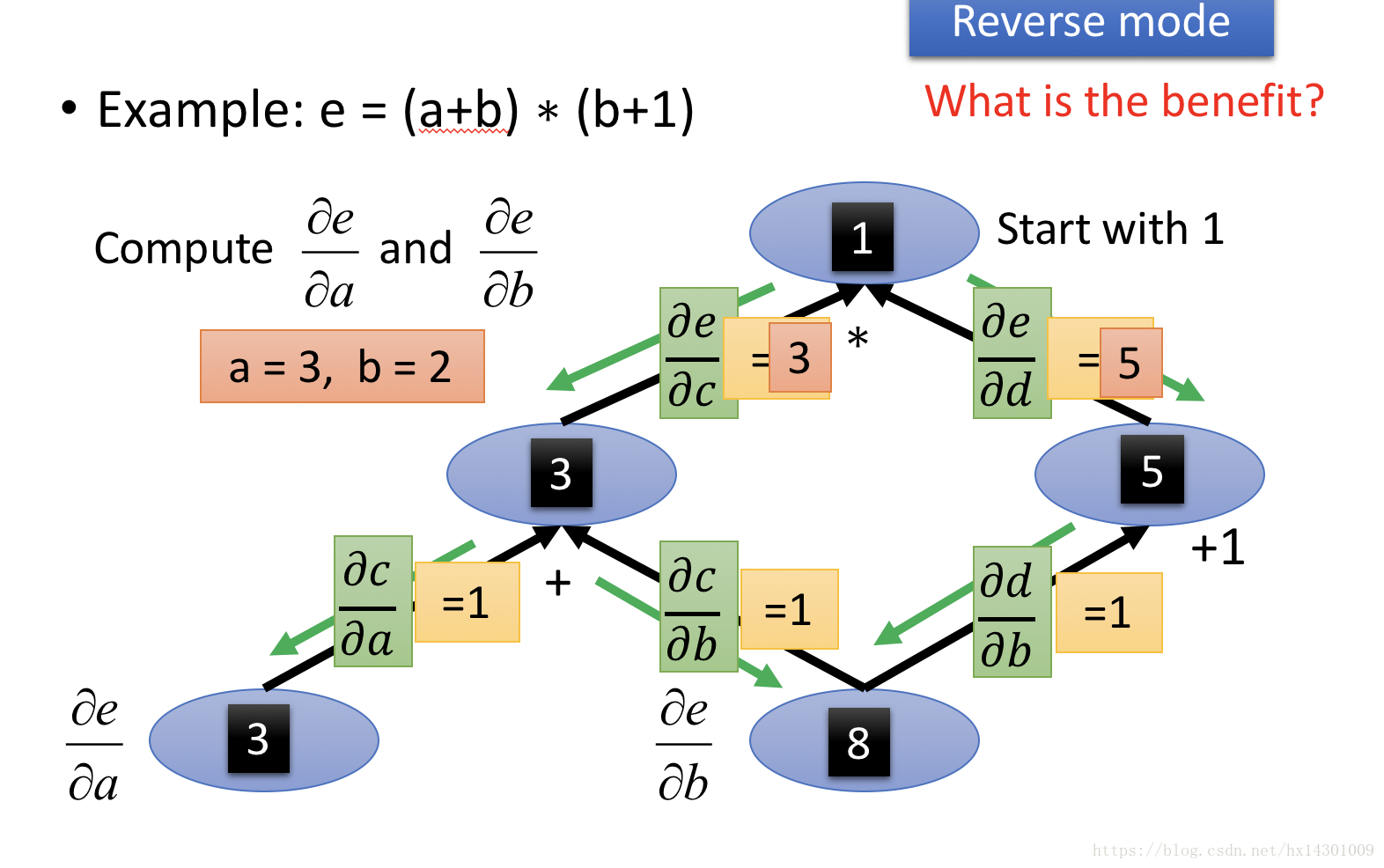
可以看到,通过这样的反向传播,每条边的偏导很快就计算出来了,这样有什么好处呢?
我们回想下在做神经网络最后的时候,都是通过一个loss function获得最后一个loss的值,这其实就可以看成是一个最后的根节点,我们要向通过loss去BP网络上各个权重的偏导,如果通过这种计算图模型来做的话,很快我们就可以将所有偏导都求出来而不会计算太多重复的偏导(如果按照传统计算方式,会设计大量重复工作)。
但是,上面这是不涉及到share weight的情况下,回想下我们的CNN,filter涉及到权重共享,我们的RNN,各个时间点上的WEIGHT也是共享的,这时候怎么用computational graph来做呢?
我们举个简单的例子来说明:
首先,依然按照计算的步骤将计算图画出,可以看到,上图的x出现在3个节点上,但是都是同一个x,也就是权重共享的情况。
开始计算各个边的偏导的时候,我们暂时将所有共享的x都视为不同的x,比如计算V对x的偏导的时候,如果按照常理来算:
V=X^2,那么偏导应该是2X,但是在图中我们需要将各个X都看成不同的X,所以这里应该看成:V=X1 * X2,所以计算出偏导为X2,也就是X。按照这种思想,可以得到上图的结果。
然后我们将各条从终点链接到X的路径的权重再加起来就是结果了。(比如上图,有3条路连接到X,那么我们分别算出3条路的导数之后,再加起来即可)
2.NN中的计算图模型
接下来我们看点复杂的:
还记得典型的神经网络是怎么正向传递值的吗?如下图:
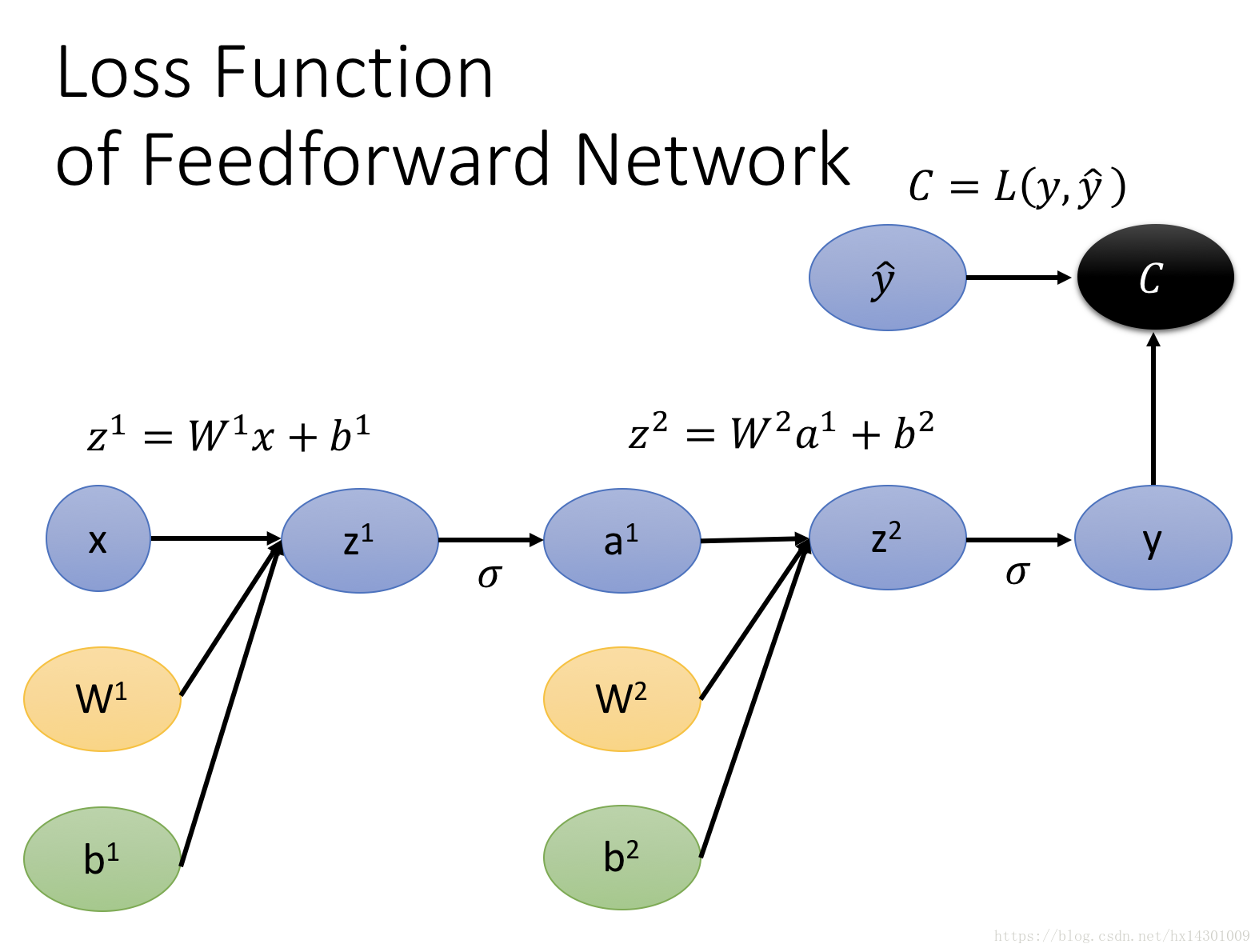
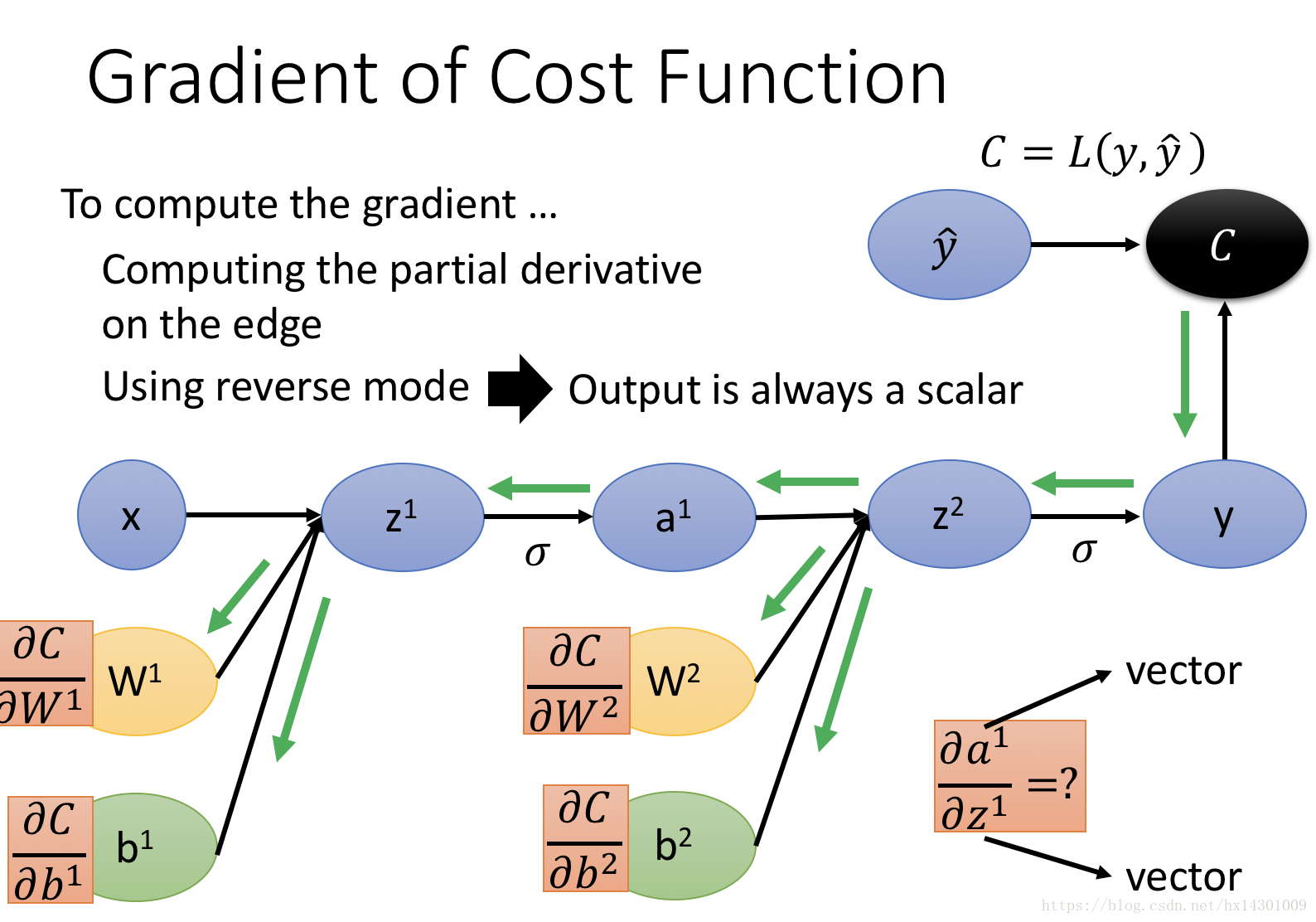
y的表达式就是上面那样,如果画成计算图模型,就是那样,但是上面的图还不够完整,因为我们的loss最终要通过一个loss function得出,然后再开始BP,因此,完整的神经网络计算图应该如下所示:
好勒,现在我们怎么来计算各个W b的梯度呢?老规矩,我们先通过forward 来计算出各个节点的值,接着我们从root开始(也就是上图的C),来计算出各条边的偏导:
注意到,在NN中,很多时候我们求偏导的并不是一个简单的数,而是一个向量Vector,那么怎么对Vector做偏导呢?这就要引入我们的Jacobian Matrix,这个东西很简单,看一个图就明白了:
如图:两个向量求偏导,会得到一个矩阵,这个矩阵的高是y的维数,宽是x的维数,内容就是图上画的。
知道了这个,我们来实际算算一些神经网络的偏导:
解释一下:当loss function是Cross Entropy loss的时候,则我们的C对y求偏导会是什么呢?
注意到,我们神经网络输出的y是一个列向量,每个yi代表属于i类别概率,而我们的CrossEntropyLoss只关注真实类别的概率,也就是:C=-logyr 其中r表示真实类别是r,因此这个表达式只和yr有关,根据jacobian matrix的计算公式,我们可以知道,C对y求偏导=一个向量[]1✖️n , n是y的维度,由于C只和yr相关,因此这个向量只有一个数不为0,即当i=r时,C对yr求偏导不为0,我们很容易算出此时为-1/yr (就是logyr的导数嘛)。
接着,我们再看一个关键点的偏导计算:
上图显示了当Z通过激活函数之后获得y,那么y对Z的偏导是什么呢?
因为Z与y都是向量,根据jacobian matrix,我们可以知道此时获得的偏导就是一个Jacobian Matrix。
这个matrix'的尺寸如图所示。
假如这里的激活函数是sigmoid,那么yi只和Zi相关,此时获得的Jacobian matrix应该是一个对角矩阵,如图、
如果我们用的是softmax作为激活函数层,那么获得的矩阵就不是对角矩阵了。
继续走:
我们来计算Z对a的偏导,根据Z=Wa的公式可以看出,对于jacobian matrix中的一个位置ij,Zi对aj求偏导应该=Wij
因此Z对a求偏导获得的jacobian matrix即为W。
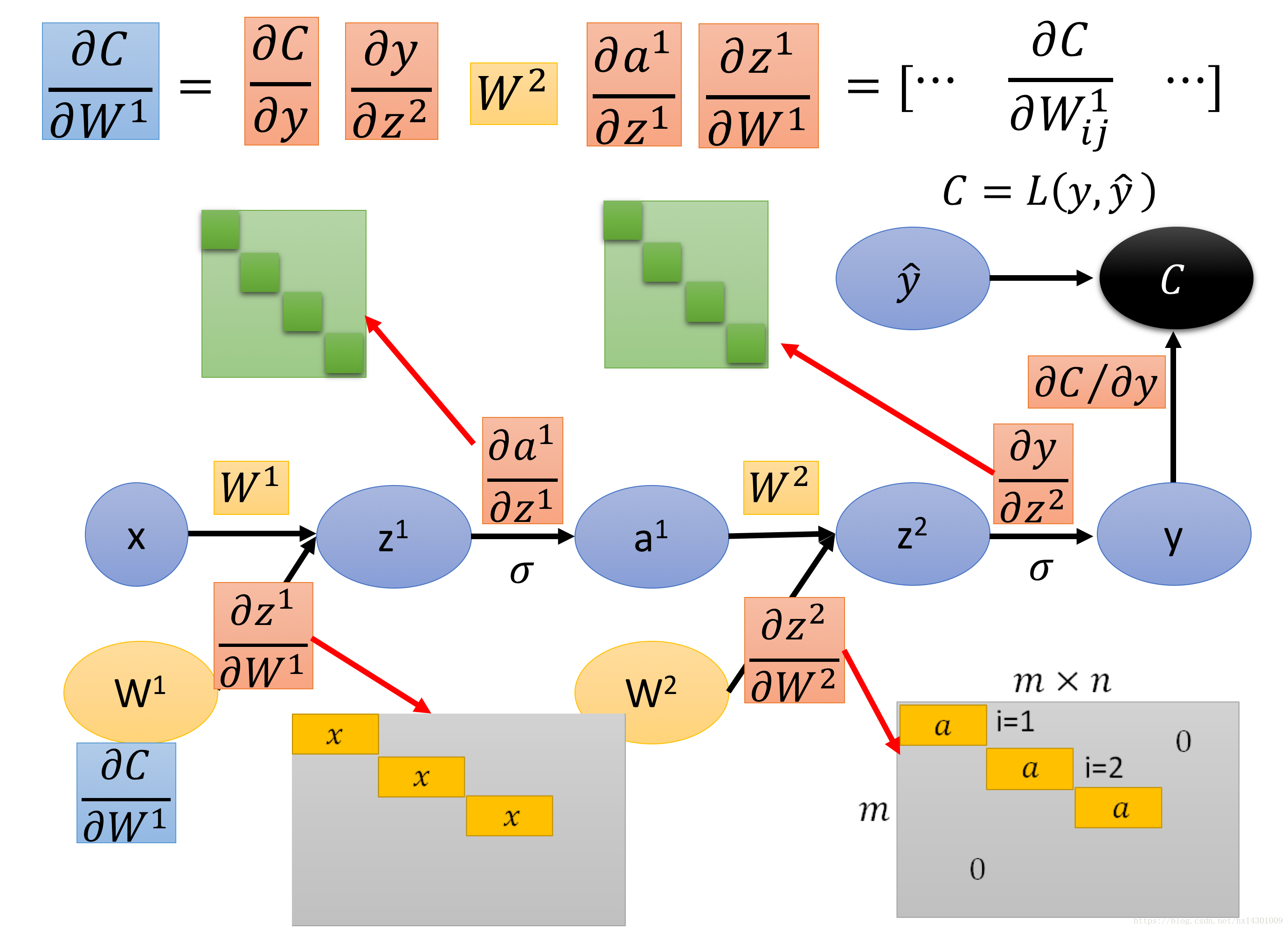
下面我们来看看Z对W求偏导:
向量对矩阵求偏导????闻所未闻。没关系,我们这里将矩阵当成一个m*n的向量来看待:
则获得的仍然是一个jacobian matrix,他的高是m,他的宽是m*n,很难想象对吧,没事,我们这里只是为了理解。
那么Zi对Wjk的导数是???根据公式可以看出,只有当i=j时,偏导才不为0,所以答案很显然了。
这样,我们来整理下最后结果:
就把偏导一路乘起来即可。
下面我们看看在rnn中怎么画这个计算图:
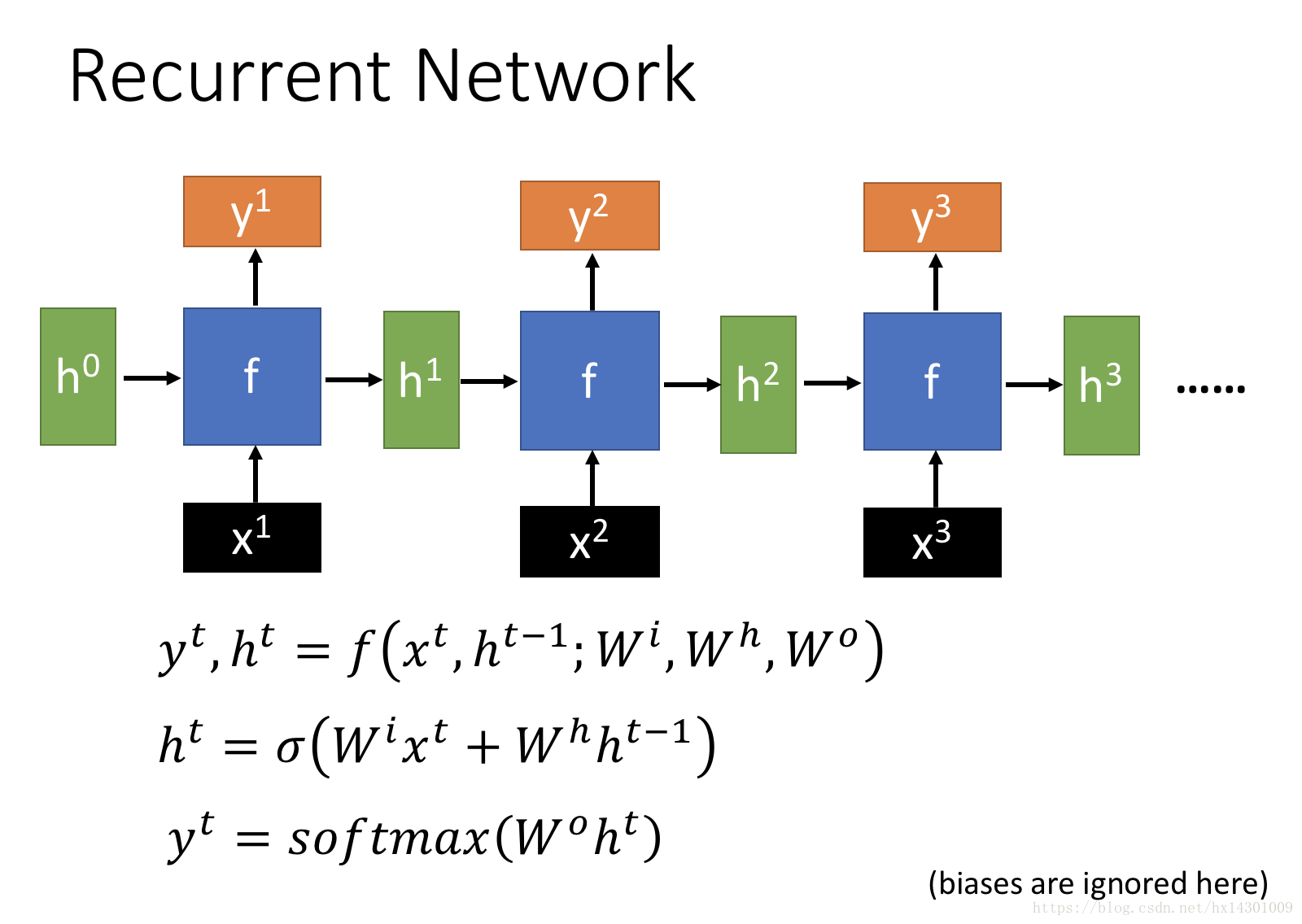
回顾下RNN的样子:
经典图,不多说
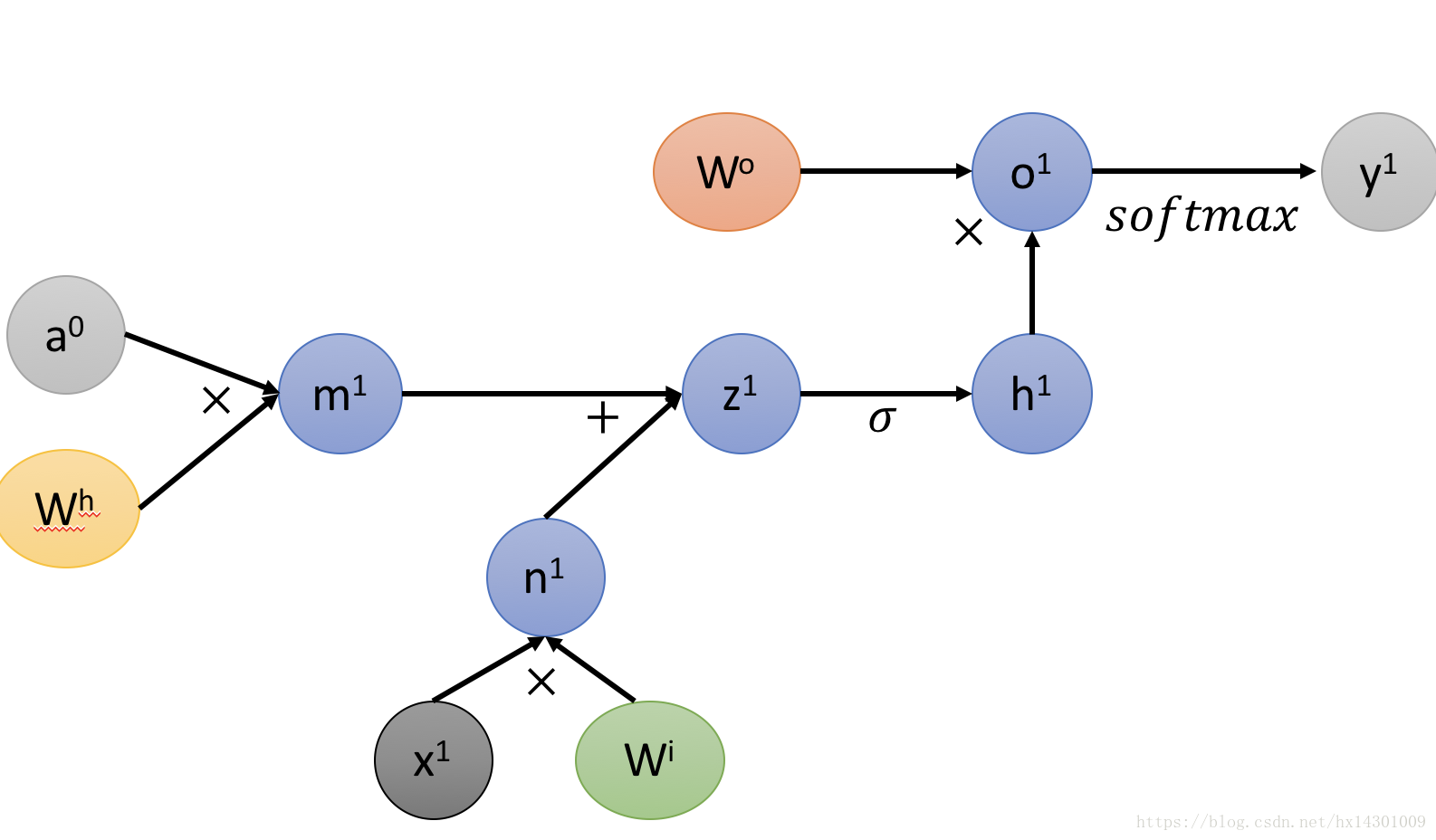
那么一个时间节点的computational graph如下图所示:
对于多个时间节点,我们可以按照这样继续画,为了直观,我们下面将几个小函数合并:
按时间维度展开,则在多个时间节点上的图就会变成这样:
(!!!高能来袭)
是不是眼花缭乱的感觉,其实没什么,就是按照时间维度展开了3个时间节点,然后我们要算的最终loss就是各个时间点的loss的和。
现在,我们开始按照BPTT进行反向传播:
恐怖如斯~~~~~
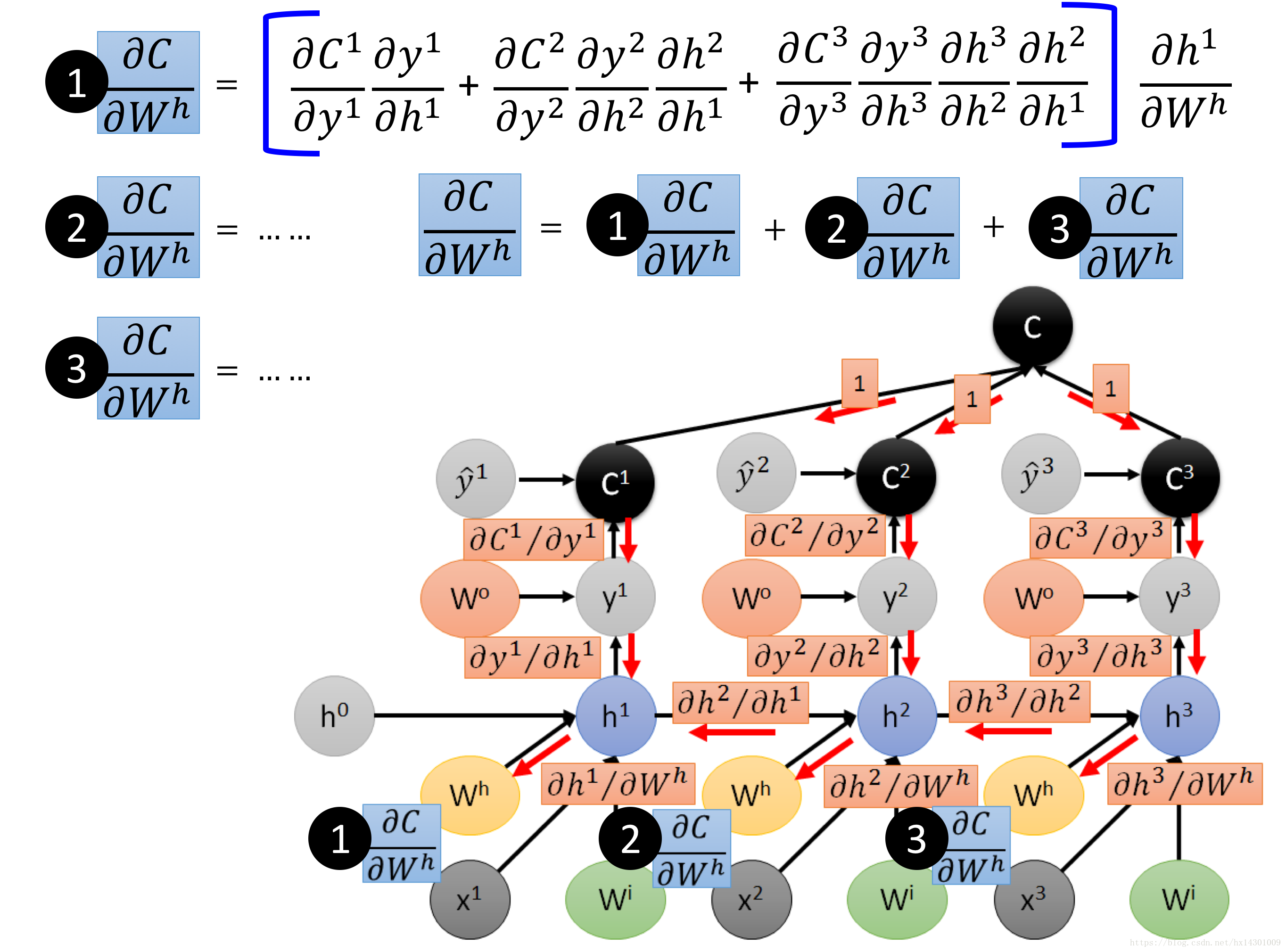
但是依稀可见是吧。举个例子,比如我们要算C对Wh的偏导,注意Wh在各个时间点上都出现过,则我们最后的偏导就应该是这3条路的偏导的和。
对于最右边那一条路,最简单的,一条路走下来乘起来就好,对于中间的Wh,它的来源有2点,第一个是C2的路下来,第二个是C3经过h3再过来,所以他的偏导是2条路加起来。然后对于最左边的Wh,它的来源就有3条路,将三条路加起来。
最后,我们再将这3条Wh都加起来,就得到C对Wh的总偏导了。虽然看起来要算很多,但是当我们将计算图用编程实现后,全程只是设计加加减减的操作,速度是很快的。 现在的主流DNN框架,计算backward用的都是计算图模型!
最后附上上面Wh偏导的图:
通过computational graph对理解BP过程很有帮助的,我们可以看到,上面对Wh偏导的公式中,设计到很多h_t+1对h_t的偏导,这个结果会得到一个矩阵,多个矩阵连乘,很容易导致梯度消失,这也是为什么RNN无法回溯太远。关于RNN更多内容,我也在慢慢学,后面再记~