矩形重叠
看过某司一道笔试题:给\(n\)个矩形左下和右上坐标(不能斜放),求重叠最多处矩形个数。
这道题本身不难:可以遍历所有矩形边界组成的点,计算该点被多少矩形包围,从而选出最大值。
由此引申出一个问题:判断两个矩形重叠。
- 如果正向思考,会有很多种情况:包含、重叠某个角、交叉...
那么如果逆向思考:什么情况两个矩形不重叠?无非就是\(A(p_1, p_2)\)在\(B(p_3, p_4)\)的上下左右:
\[(p_2.y>=p_3.y)\vee(p_4.y>=p_1.y)\vee(p_3.x>=p_2.x)\vee(p_1.x>=p_4.x) \]
取反后用De Morgan's law化简就是重叠的情况:
\[(p_2.y<p_3.y)\wedge(p_4.y<p_1.y)\wedge(p_3.x<p_2.x)\wedge(p_1.x<p_4.x) \]
线段交点
联立方程组求解当然没问题,也可以用几何的方法解:
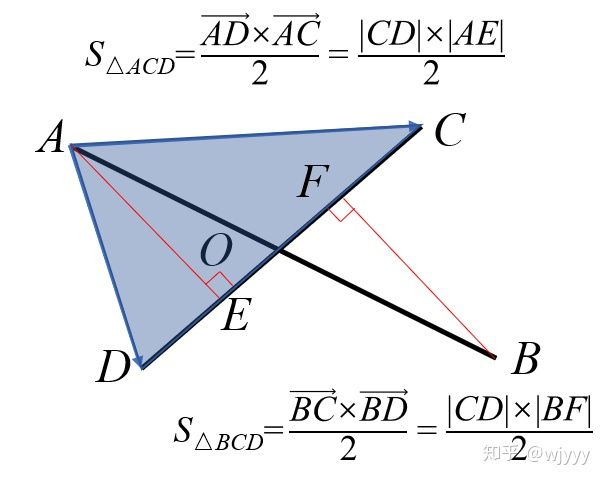
易知,\(\frac{AO}{BO}=\frac{AE}{BF}=\frac{S_{ACD}}{S_{BCD}}\),两个三角形面积可以用叉积求得,又\(\vec{AO}=\frac{AO}{AB}\vec{AB}=\frac{AO}{AO+BO}\vec{AB}\),所以\(\vec{O'O}=\vec{O'A}+\vec{AO}\),即可求得\(O\)点坐标。
向量旋转

三角变换可得:
\[\vec b=(xcos\alpha-ysin\alpha,ycos\alpha+xsin\alpha) \]
多边形面积

三角剖分:
\[S_{ABCDEF}=\frac{\vec{OA}\times\vec{OB}+\vec{OB}\times\vec{OC}+...+\vec{OF}\times\vec{OA}}{2} \]
即:
\[S=A_n\times A_1+\sum_{i=1}^{n-1}A_i\times A_{i+1}=x_ny_1-y_nx_1+\sum_{i=1}^{n-1}x_iy_{i+1}-y_ix_{i+1} \]
凸包
包围所有给定点并且周长最小的多边形。
reference
洛谷日报#142 计算几何初步