RSA算法之实现篇

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/qmickecs/article/details/39676655

序言

RSA中的密钥长度指的是公钥的长度，目前主流的公钥长度为1024、2048以及4096位。由于已经有768位公钥被成功分解的先例，所以低于1024位的公钥都被认为是不安全的。而C++自带的基本类型远远无法满足RSA的运算需求，所以RSA算法的实现必须依赖于高精度整型运算。

本文旨在介绍RSA算法的实现流程，不会对于涉及到的每一个算法进行深入介绍，如果需要进一步了解的可以参考本博客的其它相关文章。

GMP简介

GMP（the GNU Multiple Precision arithmetic library）是著名的任意精度算术运算库，支持任意精度的整数、有理数以及浮点数的四则运算、求模、求幂、开方等基本运算，还支持部分数论相关运算。Maple、Mathematica等大型数学软件的高精度算术运算功能都是利用GMP实现的。

GMP开发环境配置

Linux

直接使用sudo apt-get install libgmp-dev或yum等命令即可从软件源安装GMP。如果要使用tarball方式安装，下载GMP的源代码压缩包后运行下面的命令即可

tar xzf gmp-X.X.X.tar.xz
cd gmp-X.X.X
./configure
make 
make check
sudo make install

Windows

Windows下GMP的配置相对麻烦些，需要使用MinGW。
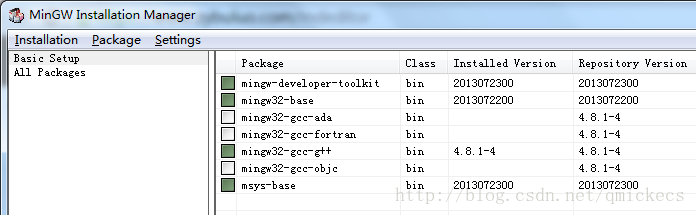
首先下载MinGW的安装管理程序MinGW Installation Manager，然后在basic setup中，将下面标记出来的几项全部右键->"Mark for Installation"

然后点击Installation->Apply Changes使更改生效。

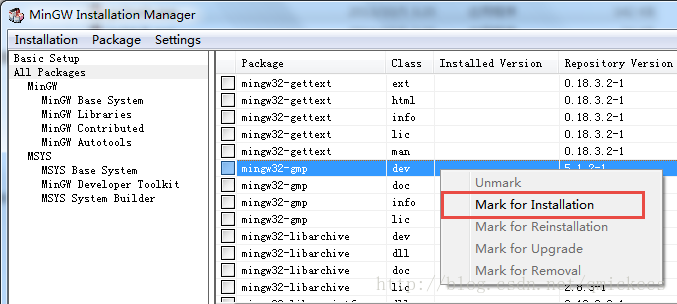
完成后，再点击All Packages，找到下图中标记出来的名字为mingw32-gmp，class属于dev的一项，同样Mark for Installation，然后Apply Changes。

GMP使用

要使用GMP，只需要包含头文件gmp.h，然后在使用gcc编译时加上参数-lgmp

GMP是一个基于C语言的开源库，其中包含了数种自定义数据类型，包括

• mpz_t 多精度整型
• mpq_t 多精度有理数
• mpf_t 多精度浮点型

GMP要求一个mpz_t类型变量在被使用前必须手动进行初始化，并且不允许对已经初始化的变量进行初始化。

下面是一些本文中使用到的部分函数，其他函数介绍以及用法请参考GMP官方文档：

mpz_t x
声明一个多精度整型变量x

void mpz_init (mpz_t x)
初始化x。任何一个mpz_t类型的变量在使用前都应该初始化。

void mpz_init_set_ui (mpz_t rop, unsigned long int op)
初始化rop，并将其值设置为op

int mpz_init_set_str (mpz_t rop, const char *str, int base)
初始化rop，并赋值rop = str，其中str是一个表示base进制整数的字符数组

void mpz_clear (mpz_t x)
释放x所占用的内存空间

void mpz_sub_ui (mpz_t rop, const mpz_t op1, unsigned long int op2)
计算op1 – op2，结果保存在rop中

void mpz_mul (mpz_t rop, const mpz_t op1, const mpz_t op2)
计算op1 * op2，结果保存在rop中

void gmp_randinit_default (gmp_randstate_t state)
设置state的随机数生成算法，默认为梅森旋转算法

void gmp_randseed_ui (gmp_randstate_t state, unsigned long int seed)
设置state的随机化种子为seed

void mpz_urandomb (mpz_t rop, gmp_randstate_t state, mp_bitcnt_t n)
根据state生成一个在范围0~2^n-1内均匀分布的整数，结果保存在rop中

char * mpz_get_str (char *str, int base, const mpz_t op)
将op以base进制的形式保存到字符数组中，该函数要求指针str为NULL（GMP会自动为其分配合适的空间），或者所指向的数组拥有足够存放op的空间

int gmp_printf (const char *fmt, ...)
语法跟C语言中的标准输出函数printf类似。它在printf的基础上，增加了mpz_t等数据类型的格式化输出功能。fmt为输出格式，例如fmt=”%Zd”时，表示输出一个10进制的多精度整型。其后的所有参数为输出的内容。

int mpz_probab_prime_p (const mpz_t n, int reps)
检测n是否为素数。该函数首先对n进行试除，然后使用米勒-拉宾素性检测对n进行测试，reps表示进行检测的次数。如果n为素数，返回2；如果n可能为素数，返回1；如果n为合数，返回0。

可以看到，GMP中的算术函数通常将保存输出结果的变量作为第一个参数，其后的参数为操作数。

下面是一个用GMP计算1+1的程序。

#include <gmp.h>

int main()
{
	mpz_t a, b, c;
	mpz_init_set_ui(a, 1);  //a = 1
	mpz_init_set_ui(b, 1);  //b = 1
	mpz_init(c);

	mpz_add(c, a, b);  //c = a + b

	return 0;
}

RSA算法实现

RSA算法大体可以分为三个部分：

• 生成密钥对
• 加密
• 解密

其中生成密钥对包括以下步骤：

• 随机生成两个足够大的素数
  p,q
• 计算公共模数n
  n=p∗q
• 计算欧拉函数
  φ(n)=(p−1)∗(q−1)
• 选取一较小的与φ(n)互质的正整数e作为公共指数。则数对(n, e)为密钥对中的公钥
• 计算
  d=e−1(modϕ(n))
  则数对(n, d)为密钥对中的私钥

生成密钥对

第一步，随机素数生成

根据著名的素数定理，我们可以知道，随机选取一个正整数n，它是素数的概率为1/ln(n)，这个概率并不算小，所以我们可以这样选取素数：随机选取一个正整数，检测它是否为素数，如果它不是素数，那我们就可以测试它邻近的正整数，直到找到一个素数为止。

比如，我们需要生成一个长度为1024位的素数，那我们先随机选取一个长度为1024位的正整数，它是素数的概率约为1 / ln(2 ^1024) ≈ 1 / 710，将偶数排除掉，进行305次测试即可找到一个素数。这样问题就转移到如何测试一个正整数是否为素数上了。

目前最常用的素性检测方法是米勒-拉宾素性检测法，这里我们使用GMP中的素数检测函数。

int mpz_probab_prime_p (const mpz_t n, int reps)

代码实现：

gmp_randstate_t grt;
gmp_randinit_default(grt); //设置随机数生成算法为默认
gmp_randseed_ui(grt, time(NULL));	//设置随机化种子为当前时间，这几条语句的作用相当于标准C中的srand(time(NULL));

mpz_t key_p, key_q;
mpz_init(key_p);
mpz_init(key_q);	//一个mpz_t类型的变量必须在初始化后才能被使用

mpz_urandomb(key_p, grt, 1024);
mpz_urandomb(key_q, grt, 1024);	//随机生成一个在0~2^1024-1之间的随机数

if(mpz_even_p(key_p))
	mpz_add_ui(key_p, key_p, 1);
if(mpz_even_p(key_q))
	mpz_add_ui(key_q, key_q, 1);	//如果生成的随机数为偶数，则加一
	
while(!mpz_probab_prime_p(key_p, 25) > 0)  //逐个检查比p大的奇数是否为素数
	mpz_add_ui(key_p, key_p, 2);
while(!mpz_probab_prime_p(key_q, 25) > 0)
	mpz_add_ui(key_q, key_q, 2);
	
gmp_printf("%ZX\n", key_p);   //以十六进制的形式输出生成的素数
gmp_printf("%ZX\n", key_q);  

第二步为简单的乘法运算，直接调用函数void mpz_mul(rop, op1, op2)

mpz_t key_n;
mpz_init(key_n);

mpz_mul(key_n, key_p, key_q); //计算p * q，并将结果储存在key_n中

第三步计算欧拉函数值也只是减法和乘法运算。

mpz_t key_f;
mpz_init(key_f);

mpz_sub_ui(key_p, key_p, 1);	//p=p-1
mpz_sub_ui(key_q, key_q, 1);	//q=q-1
mpz_mul(key_f, key_p, key_q);   //计算(p - 1) * (q - 1)，并将结果储存在key_f中

第四步，选取一个正整数e，并输出公钥(n, e)
公共指数常取3, 17和65537三个值，一般我们直接取e=65537。

mpz_t key_e;
mpz_init_set_ui(key_e, 65537);//初始化并设置e为65537

gmp_printf("%s (%ZX, %ZX)\n", "public key is:", key_n, key_e); //输出公钥(n, e)

第五步求e在模φ(n)下的乘法逆元（也被称为数论倒数）d，也就是求解未知数为d的模线性方程：

d≡e−1(modϕ(n))⇔ed≡1(modϕ(n))

转化为普通二元一次不定方程，即为

ed+kϕ(n)=1

可以证明，该方程有唯一解的充要条件是e与φ(n))互质，即gcd(e,ϕ(n))=1

方程的求解需要使用扩展欧几里德算法。

这里使用GMP中的求数论倒数的函数

int mpz_invert(mpz_t rop, const mpz_t op1, const mpz_t op2)

mpz_t key_d;
mpz_init(key_d);

mpz_invert(key_d, key_e, key_f); //求e的数论倒数d

gmp_printf("%s (%ZX, %ZX)\n", "private key is:", key_n, key_e);//输出私钥(n, d)

加密与解密

加密

计算

C=fe(M)=Memodn

，其中M为明文，(n, e)为公钥，C为密文

解密

计算

M=fd(C)=Cdmodn

，其中C为密文，(n, d)为私钥，M为明文

可以看到，加密跟解密都是对以下函数进行求值：

fb(a)=abmodn

这种形如 abmodn的运算，我们称之为 模幂运算。模幂运算在密码学中具有十分重要的意义，除了RSA加密外，离散对数加密等常用的加密方法里都有模幂运算。

对于模幂运算，很多人习惯上是先计算a的b次幂，然后再对其取模。但如果模幂运算中的a或者b特别大，那求幂运算将非常困难。不过，根据模运算的特点，我们并不需要直接计算出a的b次方的值。这种算法叫快速模幂。

下面是算法的原理介绍

以e = 11, M = 3，为例，11的二进制形式为1011，那么我们可以把它变成以下形式： 

311=38∗32∗31

设模数n = 5。 由模运算的性质可知，我们只需要利用反复平方法计算 

3^8 mod 5，3^2 mod 5和3 mod 5的值，即可计算出3^11 mod 5的值。 

计算3 ^11 mod 5的值，我们首先计算

31mod5=3
32mod5=(31mod5)2mod5=4
34mod5=(32mod5)2mod5=1
38mod5=(34mod5)2mod5=1

之前我们得出 311=38∗32∗31
则

311mod5
=(38∗32∗31)mod5
=[(38mod5)(32mod5)(31mod5)]mod5
=(1∗4∗3)mod5
=2

这也是为什么之前选取公共指数e的时候，要选择3、17或65537的原因，它们的二进制形式分别为11, 1001, 10000000000000001。在下面的代码中，可以很直观地看到，快速模幂运算中，指数（二进制形式）中1的个数越少，计算效率越高。

下面是快速模幂算法的代码实现：

void mod_exp(mpz_t result, const mpz_t exponent, const mpz_t base, const mpz_t n)
{
	char exp[2048 + 10];
	mpz_get_str(exponent, 2, exp); //把指数e转化为二进制并储存到字符数组exp中
	
	mpz_t x, power;
	mpz_init(power); 
	mpz_init_set_ui(x, 1);  // x = 1
	mpz_mod(power, base, n); //power = base mod n

	for(int i = strlen(exp) - 1; i >= 0; i--)
	{
		if(exp[i] == '1')
		{
			mpz_mul(x, x, power);  
			mpz_mod(x, x, n);   //x = x * power mod n
		}
		mpz_mul(power, power, power);
		mpz_mod(power, power, n);  //power = power^2 mod n
	}
	mpz_set(result, x); //返回结果
}

那么加密过程的代码实现为：

mpz_t M， C;
mpz_init(C);
mpz_init_set_ui(M, 123456789);//假设明文为整数123456789

mod_exp(C, key_e, M, key_n);//加密函数，C = M^e mod n

解密：

mpz_t M2;
mpz_init(M2);

mod_exp(M2, key_d, C, key_n);//解密函数，M = C^d mod n

利用中国剩余定理加速RSA解密

中国剩余定理表明，对一个较大模数进行操作与对该模数的质因数操作是等价的。利用这个特点，我们就可以将RSA解密过程中比较大的私有指数d以及公共模数n转化为较小的两个数。利用中国剩余定理（CRT）转换到CRT域，然后进行运算，再将运算结果转化为问题域。这一点倒是和傅立叶变换在时域跟频域之间进行转换有异曲同工之妙。
具体实现方法如下：

1. 将密文X转换到CRT域
   对密文X进行运算。

   Xp≡Xmodp
   Xq≡Xmodq
   那么(Xp,Xq)为密文X在CRT域下的表示。

2. 在CRT域内进行运算
   先计算

   dp=dmod(p−1)
   dq=dmod(q−1)
   然后计算
   Yp=Xdppmodp
   Yq=Xdqqmodq
   则(Yp,Yq)为Y=Xdmodn在CRT域下的表示。

3. 将结果转换回问题域
   计算

   qinv≡q−1modp
   pinv≡p−1modq
   也就是q在模p下的数论倒数以及p在模q下的数论倒数。 结果Y为
   Y≡qinvqYp+pinvpYqmodn

很明显，这个算法中最耗时间的是第二步里的模幂运算。跟直接计算相比，该算法并没有减少乘法的计算次数，但我们成功地将每次参与乘法计算的操作数长度减少到原来的二分之一。按照目前乘法运算的时间复杂度（略低于O(n^2)）来看，操作数长度减半，速度可以提升至原来的四倍左右。
并且在这个算法中，如果没有更换密钥，dp,dq,qinvq,pinvp都是可以提前计算并保存起来的，进一步提升了运算效率。

下面是一个完整的使用RSA算法进行加密解密的程序代码，该代码在Ubuntu14.04 + g++4.8 + GMP6.0.0a下通过编译并正常运行

#include <cstdio>
#include <ctime>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <gmp.h>

#define KEY_LENGTH 2048  //公钥的长度
#define BASE 16    //输入输出的数字进制

using namespace std;

struct key_pair
{
	char * n;
	char * d;
	int e;
};

//生成两个大素数
mpz_t * gen_primes()
{										
	gmp_randstate_t grt;				
	gmp_randinit_default(grt);	
	gmp_randseed_ui(grt, time(NULL));	
	
	mpz_t key_p, key_q;
	mpz_init(key_p);
	mpz_init(key_q);

	mpz_urandomb(key_p, grt, KEY_LENGTH / 2);		
	mpz_urandomb(key_q, grt, KEY_LENGTH / 2);	//随机生成两个大整数

	mpz_t * result = new mpz_t[2];
	mpz_init(result[0]);
	mpz_init(result[1]);

	mpz_nextprime(result[0], key_p);  //使用GMP自带的素数生成函数
	mpz_nextprime(result[1], key_q);

	mpz_clear(key_p);
	mpz_clear(key_q);

	return result;	
}

//生成密钥对
key_pair * gen_key_pair()
{
	mpz_t * primes = gen_primes();

	mpz_t key_n, key_e, key_f;
	mpz_init(key_n);
	mpz_init(key_f);
	mpz_init_set_ui(key_e, 65537);	//设置e为65537

	mpz_mul(key_n, primes[0], primes[1]);		//计算n=p*q
	mpz_sub_ui(primes[0], primes[0], 1);		//p=p-1
	mpz_sub_ui(primes[1], primes[1], 1);		//q=q-1
	mpz_mul(key_f, primes[0], primes[1]);		//计算欧拉函数φ(n)=(p-1)*(q-1)

	mpz_t key_d;	
	mpz_init(key_d);
	mpz_invert(key_d, key_e, key_f);   //计算数论倒数

	key_pair * result = new key_pair;

	char * buf_n = new char[KEY_LENGTH + 10];
	char * buf_d = new char[KEY_LENGTH + 10];

	mpz_get_str(buf_n, BASE, key_n);
	result->n = buf_n;
	mpz_get_str(buf_d, BASE, key_d);
	result->d = buf_d;
	result->e = 65537;

	mpz_clear(primes[0]);   //释放内存
	mpz_clear(primes[1]);
	mpz_clear(key_n);
	mpz_clear(key_d);
	mpz_clear(key_e);
	mpz_clear(key_f);
	delete []primes;

	return result;
}

//加密函数
char * encrypt(const char * plain_text, const char * key_n, int key_e)  
{
	mpz_t M, C, n;
	mpz_init_set_str(M, plain_text, BASE); 
	mpz_init_set_str(n, key_n, BASE);
	mpz_init_set_ui(C, 0);

	mpz_powm_ui(C, M, key_e, n);    //使用GMP中模幂计算函数

	char * result = new char[KEY_LENGTH + 10];
	mpz_get_str(result, BASE, C);

	return result;
}

//解密函数
char * decrypt(const char * cipher_text, const char * key_n, const char * key_d)  
{
	mpz_t M, C, n, d;
	mpz_init_set_str(C, cipher_text, BASE); 
	mpz_init_set_str(n, key_n, BASE);
	mpz_init_set_str(d, key_d, BASE);
	mpz_init(M);

	mpz_powm(M, C, d, n);   //使用GMP中的模幂计算函数

	char * result = new char[KEY_LENGTH + 10];
	mpz_get_str(result, BASE, M);

	return result;
}

int main()
{		
	key_pair * p = gen_key_pair();

	cout<<"n = "<<p->n<<endl;
	cout<<"d = "<<p->d<<endl;
	cout<<"e = "<<p->e<<endl;

	char buf[KEY_LENGTH + 10];
	cout<<"请输入要加密的数字，二进制长度不超过"<<KEY_LENGTH<<endl;
	cin>>buf;

	char * cipher_text = encrypt(buf, p->n, p->e);
	cout<<"密文为："<<cipher_text<<endl;
	char * plain_text = decrypt(cipher_text, p->n, p->d);
	cout<<"明文为："<<plain_text<<endl;
	
	if(strcmp(buf, plain_text) != 0)
		cout<<"无法解密"<<endl;
	else
		cout<<"解密成功"<<endl;

	return 0;
}