Set Theory
Sets
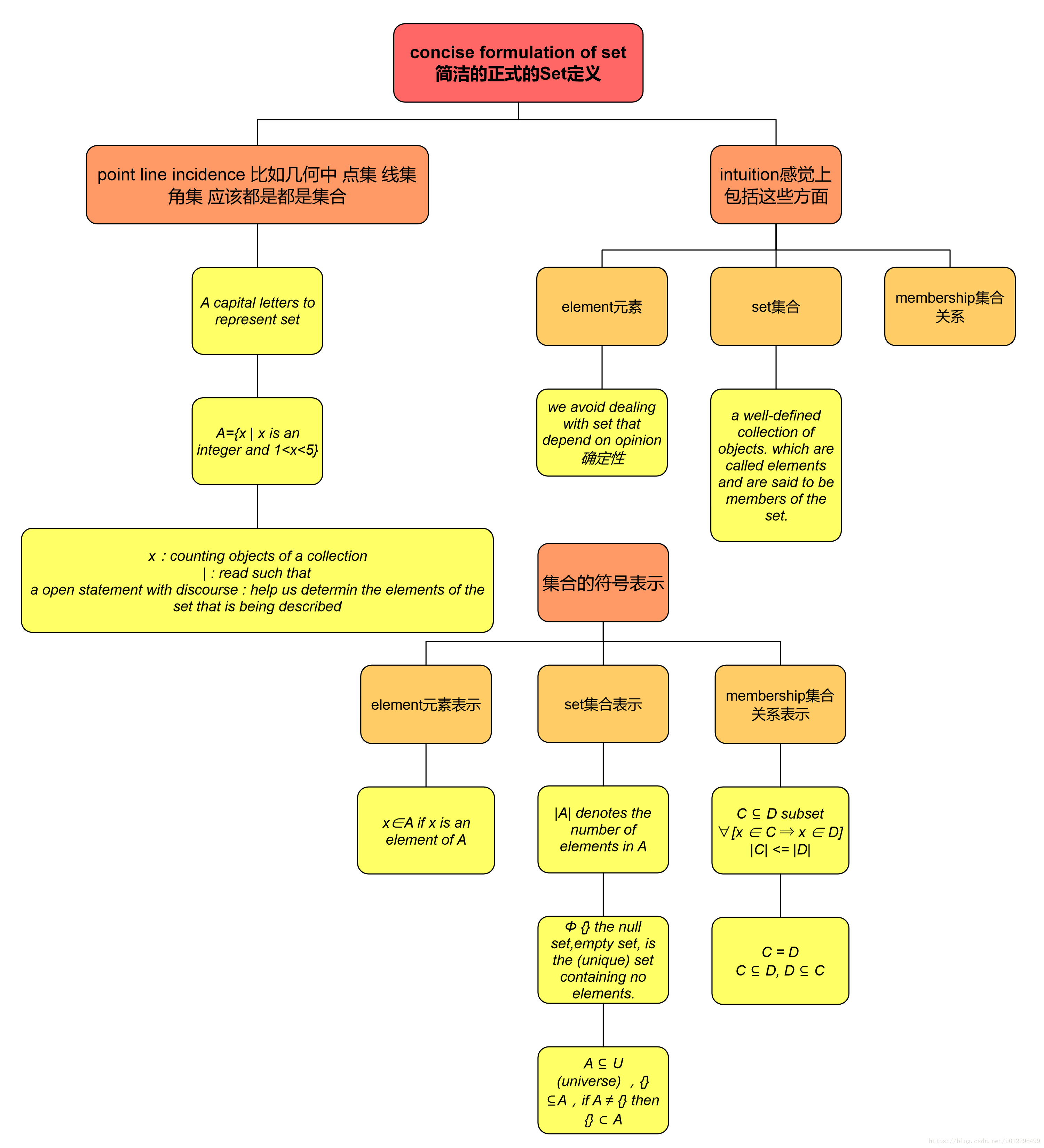
Definiion:集合定义
If A is a set from universe U, the power set of A, denoted p(A), is the collection(or set) of all subsets of A.
For any finite set A with |A| = n >= 0, we find that A has 2n subsets and that |p(A)| = 2n. For any 0 <= k <= n, there are C(n,k) subsets of size k. Counting the subsets of A according to the number, k, of elements in a subset, we have the combinatorial identity:
C(n,0)+C(n,1)+…+C(n,n)= ∑nk=0(n,k)=2n, for n>=0.
a correspondence between the compositions of a number n and the subsets of the set {1,2,3,…,n}
C(n+1, r) = C(n, r) + C(n, r-1).
(build思想1):we build a set A ={x, a1,a2,a3,…,an}
C(n+1, r) = all subsets of size r of A; C(n, r)= all subsets of size r of A without element x; C(n, r-1)= all subsets of size r-1(minus x) of A with elment x.
(build思想2):make C(n+1, r) be the paths in the xy-plane from (0, 0) to (n + 1 - r, r); C(n, r), C(n, r-1) are the two points before arrive the end point(n + 1 – r, r).
Closed operation:there are two operands, namely, a and b. Hence the operation is called binary. And since a+b ∈Z+ when a, b ∈Z+, we say that the binary operation of addition(on Z+) is closed.
子集的构建过程:GrayCode.见:GrayCode虾扯蛋。
GrayCode的build过程就像:举个栗子:n条直线最多多少交点:让新加入的直线和已有的所有直线都相交。
构建Selection from a collection选择, 与元素子集的组合的对应关系。
Set Operations:集合操作
For A, B, ⊆ U we define the following:
- A∪B (the union of A and B) = {x | x∈ A ∨ x ∈ B}.
- A∩B (the intersection of A and B) = {x | x∈ A ∧ x ∈ B}.
- A△B (the symmetric difference of A and B) = {x | (x∈ A ∨ x ∈ B) ∧ x ∉ A∩B}.
Consequently, ∪, ∩, △ are closed binary operations.
Let S, T ⊆ U. The sets S and T are called disjoint, or mutually disjoint, when S∩T = {}.
If S, T ⊆ U. then S and T are disjoint, if and only if S∪T = S△T.
For a set A⊆ U, the complement of A, denoted U-A, or A上划线, is given by {x | x ∈U ∧ x ∉ A}.
For A, B, ⊆ U, the (relative) complement of A in B, denoted B – A, is given by {x | x∈B∧x ∉ A }.
For any universe U and any set A, B ⊆ U, the following statement are equivalent:
- A ⊆ B b) A∪B=B c) A∩B=A d) B上划线⊆ A上划线
| The Laws of Set Theory |
|
| A 两个上划线 = A |
Law of Double Complement |
| A∪B 上划线 = A上划线∩ B 上划线 A∩B 上划线 = A上划线∪ B 上划线 |
DeMorgan’s Laws |
| A∪B = B∪A A∩B = B∩A |
Commutative Laws |
| A∪(B∪C) = (A∪B)∪C A∩(B∩C) = (A∩B)∩C |
Associative Laws |
| A∪(B∩C)=( A∪B)∩(A∪C) A∩(B∪C)=( A∩B)∪(A∩C) |
Distributive Laws |
| A∪A=A A∩A=A |
Idempotent Laws |
| A∪{}=A A∩U=A |
Identity Laws |
| A∪U=U A∩{}={} |
Domination Laws |
| A∪(A∩B) = A A∩(A∪B) = A |
Absorption Laws |
The dual of S, Sd , is obtained from s by replacing (1) each occurrence of {} and U by U and {}, respectively; and (2) each occurrence of ∩ and ∪ by ∪ and ∩, respectively.
Let s denote a theorem dealing with equality of two set expressions. The it’s dual of s, is also a theorem. It is only true in general not particular.
Then Venn: U is depicted as the interior of a rectangle, while subsets of U are represented by the interiors of circles and other closed cruves.
One more technique for establishing set equalities is the membership table.
Let I be a nonempty set and U a universe. For each i ∈I let AI ⊆U. then I is called an index set(or set of indices), and each i∈I is called an index.
If A and B are finite sets, then |A∪B| = |A| + |B| - | A∩B |. Consequently, finite sets A and B are(mutually) disjoint if and only if | A∪B | = |A| + |B|.
In addition, when U is finite, from DeMorgan’s Law we have |A上划线∩B上划线| = | A∪B 上划线|=|U| - | A∪B | = |U| - |A| - |B| + | A∩B |.
If A ,B and C are finite sets, then |A∪B∪C| = |A| + |B| + |C| - | A∩B | -| A∩C |- | B∩C | + | A∩B∩C |…..
Probability概率
A set of all possible outcomes for each situation is called a sample space. Each of the six possible outcomes has the same, or equal, likelihood of occurrence.
Analytic Theory of Probability:
Under the assumption of equal likelihood, let φ(fai Phi) be the sample space for an experiment ξ(克西). Each subset A of φ, including the empty subset, is called an event. Each element of φ determines an outcome, so if |φ|=n and a∈φ, A⊆φ, then
Pr({a}) = The probability that {a} (or , a) occurs = |{a}|/φ = 1/n, and
Pr(A)=The probability that A occurs = |A|/|φ| = |A|/n.
Eg: about φ : to take care of the class rabbit, she may make her selection in C(20, 2) = 190 ways. So |φ| = 190.
For sets A, B, the Cartesian product, or cross product, of A and B is denoted by A X B and equals {(a, b) | a∈A, b∈B}.
The sample space can be represented pictorially with a tree diagram that exhibits all the possible outcomes of experiment ξ.
Each element a∈φ is called an outcome or elementary event, we let Pr({a}) = Pr(a) denote the probability that this outcome occurs.
Let φ be the sample space for an experiment ξ. If A, B are any events---that is, {}⊆A,B⊆φ (so we now allow the empty set to be an event), then
- Pr(A) >=0
- Pr(φ) = 1
- If A, B are disjoint( or, mutually disjoint) then Pr(A∪B) = Pr(A) + Pr(B).
The Rule of Complement. Let φ be the sample space for an experiment ξ. If A is an event(that is , A⊆φ), then
Pr(A上划线) = 1 – Pr(A).
Independent of the outcome .Such two-outcome occurrence is called a Bernoulli trial. If there are n such trials and each trial has probability p of success and probability q (=1-p) of failure, then the probability that there are (exactly) k successes among these n trials is
C(n, k) pkqn-k, 0<=k<=n.
The Additive Rule: If φ is the sample space for an experiment ξ, and A, B⊆φ, then Pr(A∪B) = Pr(A∩B上划线) + P(B) = Pr(A) + Pr(B) – Pr(A∩B).
If φ is the sample space for an experiment ξ and A, B ⊆φ, then the conditional probability of B given A = Pr(B|A) = Pr(B∩A)/Pr(A), so long as Pr(A) <> 0.
Law of Total Probability. Pr(B) = Pr(A)Pr(B|A) + Pr(A上划线)Pr(B|A上划线)
Given a sample space φ with events A,B ⊆φ, we call A, B independent when Pr(A∩B) = Pr(A)Pr(B).
Decide when A, B are independent:
- Pr(A∩B) = Pr(A)Pr(B)
- Pr(A|B) = Pr(A) or
- Pr(B|A) = Pr(B)
Let A, B be events taken from a sample space φ, If A, B are independent, then A,B上划线 are independent; A上划线, B are independent; and A 上划线 , B上划线 are independent.
For a sample space φ and events A, B, C ⊆φ, we say that A, B, C are independent if
- Pr(A∩B) = Pr(A)Pr(B);
- Pr(A∩C) = Pr(A)Pr(C);
- Pr(B∩C) = Pr(B)Pr(C);
- Pr(A∩B∩C) = Pr(A)Pr(B)Pr(C);
We define the random variable X as X(x1x2x3x4) counts the number of ? that appear among the four components x1,, x2, x3, x4.
E(x) = ∑x·Pr(X=x)(期望)
Among n Bernoulli trials.
E(x) = ∑x(x=0,n)·Pr(X=x) = ∑x(x=0,n) C(n,x)pxqn-x = np.
Eg:一次性摇6个色子,摇到6点的期望是6*1/6=1;
The variance of X, Var(X)
Var(X) = E(X – E(X))2 = ∑x (x – E(x))2 · Pr(X = x)
Among n independent Bernoulli trials. The Var(X) = npq;
同理:我们举个栗子:
- 比如,聚个餐之类的东西,大家都熟悉晒。比如有一次,我找人说,我们打架了,人家回答说:没关系,一起吃个饭喝个酒就什么事都没有了。那么我就以一起吃个饭为例。
- 嗯elements: 领导,我,同事1, 同事2, 同事3, 甲方领导,甲方同事1,甲方同事2,之类的。
- Determin: 这些个人吃饭不付钱,额,关键不在于 不付钱,关键在于那些人参与了吃饭。额,关键也不在于吃饭,关键在于到场参加了吧。
- 这里我们有各种各样的子集 比如 {年轻人子集} ,{领导子集}, {甲方子集},{湖南人子集},…. 这些人都吃晚饭不用付钱。(关键不在钱 ^………^)。
- 我们乙方都是湖南人。
- 我们吃饭时发表了各自不同的看法。自由谈论{同事1和同事2在讨论历史}、{同事3在给所有到场人员轮流敬酒}、{甲方领导在吹牛逼}、{我在埋头挑豆子吃}。这些都是全集U的子集。
- 甲方席间提出:吃完饭后甲方将利用他们的几个同事,在甲方测试员甲方同事1的带领下,外在招聘几个同事,组成一个测试小组,验收工程结果。
- 乙方对甲方的测试小组组建要求表示满意,并委派 同事3 协同测试小组共同完成测试任务。{同事3} * 处理 {乙方测试小组} 提出的问题。
- 乙方我们到场的几个开发人员中,有三个是Java开发,一个是C语言开发;我们一共四个开发,但是我们三个需要完成web端开发任务。
- 到场的几个人中,有四个不吃辣椒,三个不吃牛肉,还有四个不吃饭,有一个啥都没有吃。有一个既不吃辣椒也不迟牛肉。(所以他不吃花椒牛肉)之类的。
- 吃完后,服务员第一次催结账领导表示银行卡被锁死,第二次催结账同事表示没带钱,第三次大家表示要去如厕,之类的。
- 服务员表示 你们这么多人吃一盘菜,需要按人头数加钱,第一桌有6个人,第二桌有….,其中第一桌的同事1表示两桌他都有吃。
- 吃完后桌上剩余 {一瓶82年的茅台,一盆牛肉,一盒花生米,一杯82年的啤酒}大家纷纷表示要打包带走。领导指派其中的两个人负责打包,我被选中的概率是1/n
- 我被选中打包,并分到打包花生米,边走边吃,到家能吃完的概率是1/4 * 1/n *1= 1/4n。
- {剩余的菜} * {打包的人} = 笛卡儿积。
- 假设提着茅台的人 提不动牛肉,那么我吃到花生米的概率是?不知道。
- 我能吃到花生米的期望是?无穷大。
- Probability定义了event的概念,而我们在某程序中也大量的存在event。Spring中也有专门的事件监听模块实现。