目录
线性代数回顾
曲线概念
线性代数回顾
我们要开始接触直线斜率的概念了,证明了开始要学习导数了,
这里我们会做一个自理,顺便回顾一下线性代数的知识。
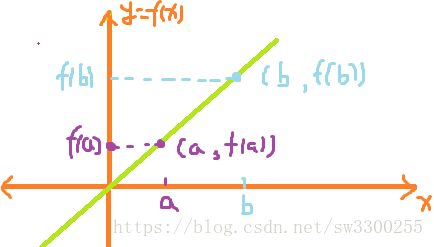
怎么求一条直线的斜率呢?如图:
首先,这个直线方程是:f(x) = mx + b。(其实m就是斜率)
我们的方法是在直线取两点:
x = a,把a代入方程,所以y=f(a)。
x = b,把b代入方程,所以y=f(b)。如图:
那我们怎么求两点的斜率?也就是求这条直线的斜率。
(注意:直线任意点的斜率都是同一个常数)
斜率等于上高度比上跨度。如果你刚学线性代数时你们会看这个定义。
另一种方法:斜率等于y增量比上x增量。我们使用这个公式来求出斜率:
首先,是多少?也就是 y 的增量是多少?
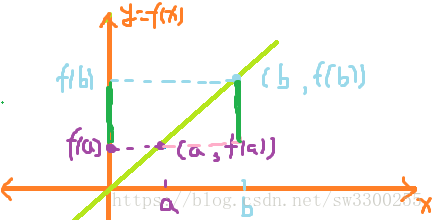
我们在图中可以看到 y 的增量,其实就是这里(绿色的线):
它就是,所以
。
那么,是多少?也就是 x 的增量是多少?
我们在图中可以看到 x 的增量,其实就是这里(红色的线):
它就是,所以
。所以我们得到:
把它们代到这里来计算就得到斜率了。这是很简单的。
现在我们a上面的点坐标设置为(3,4),b上面的点坐标设置为(6,8)。
如果我们要求直线的斜率:
得出斜率为4/3。
曲线概念
下面我们继续推广斜率的定义,也就是我们探究微积分时,将会学到新的概念。
我们要把这个斜率推广到曲线。
什么是曲线的斜率?
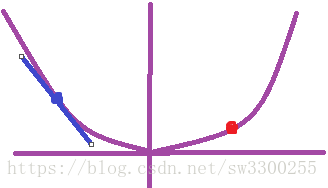
我们先画个曲线,方程是y = x^2 ,如下一个曲线图:
假设我们要具体求出这一点的斜率:
事实上,求某一点的斜率之前,我们必须先弄懂什么是曲线的斜率。
我们知道,直线的斜率是一直不变的。但对于曲线,它的斜率是变化的。
以上图上的那一点的斜率就是该点切线的斜率。就是刚好与曲线相切的直线,这的斜率就是这一点的斜率。如图:
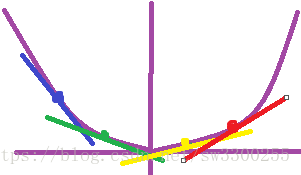
这一点的斜率是负数。然后这点,它的斜率也是负的,但是这个负数的绝对值稍小。就像这样:
接着正向增加,斜率又变成递增了,我在画另一条切线,如图:
直线的斜率是不变的,你可以在直线上取任意两点,然后求出y和x的增量之比,就得到整条直线的斜率了。
但你们已经看到对于曲线,求它的斜率就稍微不同了。
我们来做个试验:
如果这时我想求这一点的斜率,我们该怎么做?
根据斜率的定义,求斜率需要两个坐标点。只有一个点的话,我们不知道怎么求斜率。
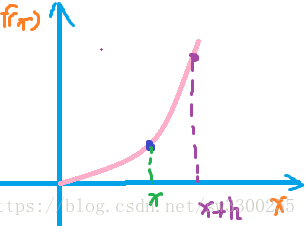
我们先令这一点的横坐标为x,我们取一个稍微大一点的点。如图:
那么,它们在曲线上的纵坐标是多少?曲线方程是y = f(x)。
那么这相当接近的两点,它们之间的斜率是多少呢?
请记住,现在求的还不是这一点的斜率,现在求的是这两点连线的斜率。割线和曲线相交两点:
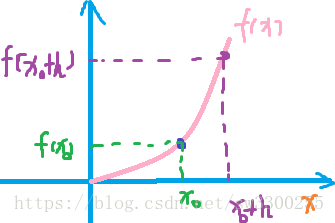
我放大图那两点之间的图:
下面橙色点的坐标是,上面绿色点的坐标是
。
不管线性方程是什么,把横坐标代进去求得的就是纵坐标。
任意去两点,作为切入点。我们先问自己这条斜率是多少呢?
求直线斜率先求出y增量,然后用它比上x增量,如图:
黄色就是x和y的增量部分,然后这条割线的斜率是多少呢?我们根据公式得出:
我们先把它简化一下:
我们定义坐标的时候是令第二点比第一点大某个数h,而我们有一种叫"极限"的数学工具。
h是个一般化数据,可以是任何数。至少理论上是可以假设的。
如果令h无限趋近于0会怎么样?
首先,这里h可能是一个很大的数,但如果我令h变小一点,任何我们求这条新割线的斜率,如图:
然后继续令h变小一点,又求一次新割线的斜率:
一直这样变小。当h逐渐趋近与0,我求出的割线斜率就越来越接近,一直到所要求的那个点的切线的斜率了。
显然,如果h很大割线的斜率和那个确切的点的斜率相差十万八千里。
但如果h是0.00000001的话,两个斜率就非常接近了。
所以,我取 h 趋于0这一极限会怎么样呢?
(有教材把h写成,是一样的。)
我们就令该表达式为这点切线的斜率,这个式子我们称为f(x)的导函数,我把它写下来:
记住,曲线上的每一点斜率都不一样。不管你取什么x值,它都对应一个不同的斜率。
现在可以利用这个公式,把任意x值代入,求出那一点斜率。
——请不断重复练习、练习、练习、再练习。。。