SVM——硬间隔最大化

本文参考自http://cs229.stanford.edu/notes/cs229-notes3.pdf，但采用《统计学习方法》中的符号系统

数据集$D=\left \{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)}) \right \}$，$x^{(i)} \in \mathbb{R}^n$，$y^{(i)}\in \{-1, 1\}$

超平面$w^Tx+b=0$，$w\in \mathbb{R}^n$，$b\in \mathbb{R}$

假设数据集$D$线性可分，则存在超平面$w^Tx+b=0$，当$y^{(i)}=1$时，$w^Tx^{(i)}+b>0$，当$y^{(i)}=-1$时，$w^Tx^{(i)}+b<0$

【立体几何知识】

点$(x_0,y_0,z_0)$到平面$Ax+By+Cz+D=0$的距离为

$\begin{aligned}d=\frac{\left | Ax_0+By_0+Cz_0+D \right |}{\sqrt{A^2+B^2+C^2}}\end{aligned}$

【几何间隔】

类似的，样本点$(x^{(i)},y^{(i)})$到超平面$w^Tx+b=0$的距离$\begin{aligned}\gamma^{(i)}=\frac{\left | w^Tx^{(i)}+b \right |}{\left \| w \right \|}\end{aligned}$，称为几何间隔

利用标签$y^{(i)}$可去掉分子的绝对值符号，得到$\begin{aligned}\gamma^{(i)}=\frac{y^{(i)}\ (w^Tx^{(i)}+b)}{\left \| w \right \|}\end{aligned}$

对于数据集$D$，所有样本的几何间隔中的最小值，$\gamma_D = \min \left\{ \gamma^{(1)}, \gamma^{(2)}, ..., \gamma^{(m)} \right\}$，称为超平面$w^Tx+b=0$关于数据集$D$的几何间隔

【CS229上关于几何间隔的证明】


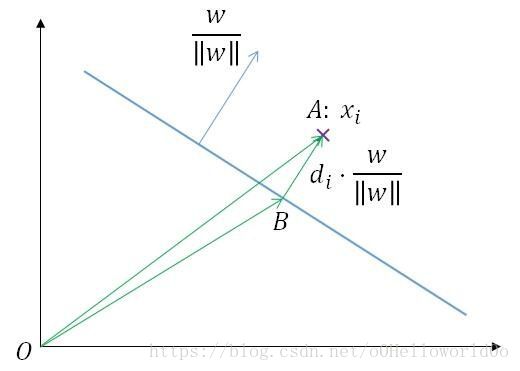
如图所示，$\begin{aligned}\frac{w}{\left \| w \right \|}\end{aligned}$为分类超平面$wx+b=0$的单位法向量，向量$\overrightarrow{OA}$的坐标（也是点$A$的坐标）为$x_i$，样本$x_i$离超平面的距离为$d_i$，则向量$\overrightarrow{BA}$的坐标为$\begin{aligned}d_i \cdot \frac{w}{\left \| w \right \|}\end{aligned}$

于是$\overrightarrow{OB} = \overrightarrow{OA} - \overrightarrow{BA}$，即向量$\overrightarrow{OB}$的坐标（也是点$B$的坐标）为$\begin{aligned}x_i - d_i \cdot \frac{w}{\left \| w \right \|}\end{aligned}$

由于点$B$在超平面上，代入超平面方程，得$\begin{aligned}w \left ( x_i - d_i \cdot \frac{w}{\left \| w \right \|} \right ) + b = 0\end{aligned}$

解得$\begin{aligned}d_i = \frac{wx_i+b}{\left \| w \right \|}\end{aligned}$

【函数间隔】

超平面$wx+b=0$关于样本点$(x_i,y_i)$的函数间隔定义为几何间隔的$\left \| w \right \|$倍，即$\gamma = y_i(wx_i+b)$

对于数据集$D$，所有样本的函数间隔中的最小值，$\gamma_D=\min \left\{ \gamma_1, \gamma_2, ..., \gamma_n \right\}$，称为超平面$wx+b=0$关于数据集$D$的函数间隔

函数间隔与几何间隔的关系为$\begin{aligned}d_i = \frac{\gamma_i}{ \left \| w \right \| }\end{aligned}$

【间隔最大化】

SVM的目标是寻找一个几何间隔最大的超平面，最优化问题表达如下：

$\begin{aligned}\max \limits_{w, b} \ d_D \quad \text{s.t.} \ \frac{ y_i \left( wx_i + b \right) }{ \left \| w \right \| } \geqslant d_D\end{aligned}$

代入$\begin{aligned}d_D = \frac{\gamma_D}{ \left \| w \right \| }\end{aligned}$，将几何间隔替换为函数间隔

$\begin{aligned}\max \limits_{w, b} \ \frac{\gamma_D}{ \left \| w \right \| } \quad \text{s.t.} \ \frac{ y_i \left( wx_i + b \right) }{ \left \| w \right \| } \geqslant \frac{\gamma_D}{\left \| w \right \|}\end{aligned}$

化简$\text{s.t.}$部分，得

$\begin{aligned}\max \limits_{w, b} \ \frac{\gamma_D}{ \left \| w \right \| } \quad \text{s.t.} \ y_i \left( wx_i + b \right) \geqslant \gamma_D\end{aligned}$

现在分析一下$\gamma_D$对最优解的影响

当$\gamma_D=1$时，得到一组最优解$w^*_1$，$b^*_1$，当$\gamma_D=2$时，得到一组最优解$w^*_2$，$b^*_2$

这两组最优解的关系为：$w^*_2 = 2w^*_1$，$b^*_2 = 2b^*_1$，是成比例的，所以将$\gamma_D$取一个特殊值即可，此处取$\gamma_D=1$，于是得到

$\begin{aligned}\max \limits_{w, b} \ \frac{1}{ \left \| w \right \| } \quad s.t. \ y_i \left( wx_i + b \right) \geqslant 1\end{aligned}$

因为$\begin{aligned}\max \limits_{w, b} \ \frac{1}{ \left \| w \right \| }\Leftrightarrow\min \limits_{w, b}\ \left \| w \right \| \Leftrightarrow\min \limits_{w, b}\ \left \| w \right \|^{2} \Leftrightarrow\min \limits_{w, b}\ \frac{1}{2} \left \| w \right \|^{2}\end{aligned}$

所以得到最终的线性可分SVM的最优化问题为：

$\begin{aligned}\min \limits_{w, b}\ \frac{1}{2} \left \| w \right \|^{2} \quad \text{s.t.} \ y_i \left( wx_i + b \right) \geqslant 1\end{aligned}$

我们已经得到了SVM的原始问题

$\begin{aligned}\min \limits_{w, b}\ \frac{1}{2} \left \| w \right \|^{2}\end{aligned}$

$\text{s.t.} \ 1 - y_i \left( wx_i + b \right) \leqslant 0$

这个问题属于凸二次规划问题，已经可以使用相关的算法包来求解了，但是《机器学习》（周志华）中说“我们可以有更高效的解法”，这个更高效的解法就是转而去解原始问题对应的对偶问题

对于SVM，原始问题和对偶问题是等价的（$d^*=p^*$），所以求得了对偶问题的最优解$d^*$，就相当于得到了原始问题的最优解$p^*$

【SVM的对偶问题】

对偶问题都是从定义拉格朗日函数开始的

$\begin{aligned} L(w,b,\alpha) &= \frac{1}{2} \left \| w \right \|^{2}+\sum_{i=1}^{n}\alpha_i \left [ 1-y_i\left ( wx_i+b \right ) \right ] \\ &=\frac{1}{2} \left \| w \right \|^{2}-\sum_{i=1}^{n}\alpha_i y_i\left ( wx_i+b \right )+\sum_{i=1}^{n}\alpha_i \\ &=\frac{1}{2} \left \| w \right \|^{2}-\sum_{i=1}^{n}\alpha_i y_i x_iw - \sum_{i=1}^{n}\alpha_i y_ib+\sum_{i=1}^{n}\alpha_i \\ &=\frac{1}{2} \left \| w \right \|^{2}-w\sum_{i=1}^{n}\alpha_i y_i x_i - b\sum_{i=1}^{n}\alpha_i y_i+\sum_{i=1}^{n}\alpha_i \end{aligned}$

求解对偶问题实际上是求解拉格朗日函数的极大极小问题：$\max \limits_{\alpha:\alpha_i \geqslant 0} \min \limits_{w,b}L(w,b,\alpha)$
（记住对偶问题是先挑“矮个儿”再挑“高个儿”，先处理原变量，再处理对偶变量）

第一步，求$\min \limits_{w,b}L(w,b,\alpha)$，其中$w，b$为变量，$\alpha$为常量同时消去变量$w，b$

令$\begin{aligned}\nabla_w L(w,b,\alpha)=w-\sum\limits_{i=1}^{n}\alpha_i y_i x_i=0\end{aligned}$

$\begin{aligned}\quad \nabla_b L(w,b,\alpha)=-\sum\limits_{i=1}^{n}\alpha_i y_i=0\end{aligned}$

得$\begin{aligned}w=\sum\limits_{i=1}^{n}\alpha_i y_i x_i\end{aligned}$

$\begin{aligned}\quad\sum\limits_{i=1}^{n}\alpha_i y_i=0\end{aligned}$

上述2个式子的意义略有区别，式1中可将变量$w$用变量$\alpha$代替，而式2却不包含变量$b$，是一个实实在在的约束条件，需要将该约束条件带到第二步中

但不管怎样，将上述2个式子代入$L(w,b,\alpha)$中，总可以消去变量$w$，$b$
（注意：在第2项中，当代入$\begin{aligned}w=\sum\limits_{i=1}^{n}\alpha_i y_i x_i\end{aligned}$时，因为$L(w,b,\alpha)$中使用过了下标$i$，因此需要把下标$i$换为$j$）

$\begin{aligned}\min \limits_{w,b}L(w,b,\alpha) &=\frac{1}{2} \left \| w \right \|^{2}-w\sum_{i=1}^{n}\alpha_i y_i x_i - b\sum_{i=1}^{n}\alpha_i y_i+\sum_{i=1}^{n}\alpha_i \\&= \frac{1}{2} \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\alpha_i\alpha_j y_i y_j x_i x_j-\left ( \sum\limits_{j=1}^{n}\alpha_j y_j x_j \right )\left ( \sum_{i=1}^{n}\alpha_i y_i x_i \right )-b\cdot0+\sum_{i=1}^{n}\alpha_i \\&= \frac{1}{2} \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\alpha_i\alpha_j y_i y_j x_i x_j- \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\alpha_i\alpha_j y_i y_j x_i x_j+\sum_{i=1}^{n}\alpha_i \\&=-\frac{1}{2} \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\alpha_i\alpha_j y_i y_j x_i x_j+\sum_{i=1}^{n}\alpha_i \end{aligned}$

即$\begin{aligned}\min \limits_{w,b}L(w,b,\alpha)=-\frac{1}{2} \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\alpha_i\alpha_j y_i y_j x_i x_j+\sum\limits_{i=1}^{n}\alpha_i\end{aligned}$（仅包含变量$\alpha$）

第二步，求$\max \limits_{\alpha:\alpha_i \geqslant 0} \min \limits_{w,b}L(w,b,\alpha)$，即得到如下的对偶问题

$\begin{aligned}\max \limits_{\alpha} \ -\frac{1}{2} \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\alpha_i\alpha_j y_i y_j x_i x_j+\sum\limits_{i=1}^{n}\alpha_i\end{aligned}$

$\begin{aligned}\text{s.t.} \ \sum\limits_{i=1}^{n}\alpha_i y_i=0\end{aligned}$（在第一步中得到的约束条件，照抄过来）
$\quad \quad \alpha_i \geqslant 0$

因为对于原始问题，$\begin{aligned}\frac{1}{2} \left \| w \right \|^{2}\end{aligned}$和$1 - y_i \left( wx_i + b \right)$均为凸函数，没有等式约束，并且存在$(w, b)$使得所有不等式约束$1 - y_i \left( wx_i + b \right) \leqslant 0$成立（因为规定了数据集线性可分）

所以存在一组$(w^*, b^*, \alpha^*)$，满足$p^*=d^*=L(w^*, b^*, \alpha^*)$

故求解对偶问题等价于求解原始问题，即求解对偶问题得到的最优解其实就是原始问题的最优解

【KKT条件】

原问题的约束
①$\ 1-y_i \left( wx_i + b \right)\leqslant 0 \quad i=1,2,\cdots,n$

梯度等于0
②$\ \begin{aligned}\nabla_w L(w,b,\alpha)=0\Rightarrow w=\sum\limits_{i=1}^{n}\alpha_i y_i x_i\end{aligned}$
③$\ \begin{aligned}\nabla_b L(w,b,\alpha)=0\Rightarrow \sum\limits_{i=1}^{n}\alpha_i y_i=0\end{aligned}$

不等式约束的拉格朗日乘子大于等于0
④$\ \alpha_i \geqslant 0\quad i=1,2,\cdots,n$

对偶互补条件
⑤$\ \alpha_i \left [ 1-y_i\left ( wx_i+b \right ) \right ]=0\quad i=1,2,\cdots,n$

【求解对偶问题】

$\begin{aligned}\max \limits_{\alpha} \ -\frac{1}{2} \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\alpha_i\alpha_j y_i y_j x_i x_j+\sum\limits_{i=1}^{n}\alpha_i\end{aligned}$
$\begin{aligned}\text{s.t.} \ \sum\limits_{i=1}^{n}\alpha_i y_i=0\end{aligned}$
$\quad \quad \alpha_i \geqslant 0$

该对偶问题是凸二次规划问题，仍然可以使用现成的算法包求解，但仍然不够高效（该问题的规模正比于训练样本数——《机器学习》周志华），因此根据该问题定制了一个更高效的算法，即SMO算法

求解对偶问题（使用SMO算法），得到最优解$\alpha^*$，此时任务还没有完成，还需要利用$\alpha^*$，求出$w^*$，$b^*$

对于$w^*$，利用KKT条件②计算：$\begin{aligned}w^*=\sum\limits_{i=1}^{n}\alpha_i^* y_i x_i\end{aligned}$

对于$b^*$，有KKT条件⑤成立：中的对偶互补条件$\alpha_i^* \left [ 1-y_i\left ( w^*x_i+b^* \right ) \right ]=0$成立

对于$\alpha^*$中的一个满足$\alpha_j^*>0$的分量$\alpha_j^*$，有$\alpha_j^* \left [ 1-y_j\left ( w^*x_j+b^* \right ) \right ]=0 \Rightarrow 1-y_j\left ( w^*x_j+b^* \right )=0$

$\begin{aligned}y_j\left ( w^*x_j+b^* \right )-1&=0 \\ y_j\left ( w^*x_j+b^* \right )-y_j^2&=0 \text{（使用$y_j^2$替换1）} \\ w^*x_j+b^*-y_j&=0 \\ b^*&=y_j-x_jw^* \\ b^*&=y_j-x_j\sum_{i=1}^{n}\alpha_i^* y_i x_i \text{（代入$w^*=\sum_{i=1}^{n}\alpha_i^* y_i x_i$）} \\ b^*&=y_j-\sum_{i=1}^{n}\alpha_i^* y_i x_i x_j \end{aligned}$

综上所述，使用$\alpha^*$计算$w^*$，$b^*$的公式为
$\begin{aligned}w^*=\sum\limits_{i=1}^{n}\alpha_i^* y_i x_i\end{aligned}$
$\begin{aligned}b^*=y_j-\sum\limits_{i=1}^{n}\alpha_i^* y_i x_i x_j\end{aligned}$（样本$(x_j,y_j)$对应的$\alpha_j>0$）

理论上有多少个支持向量，就能算出多少个参数$b^*$，这时，对所有$b^*$求平均值即可

计算出$w^*$，$b^*$之后，对于一个未知的样本$x_{\text{test}}$，我们需要计算$w^Tx_{\text{test}}+b$

我们仍然将$w$展开，看看会得到什么

$\begin{aligned}w^Tx_{\text{test}}+b&=\left ( \sum\limits_{i=1}^{n}\alpha_i y_i x_i \right )^T x_{\text{test}}+b \\ &=\sum\limits_{i=1}^{n}\alpha_i y_i \left \langle x_i, x_{\text{test}} \right \rangle + b \end{aligned}$

我们发现，除了支持向量以外的$\alpha_i$都是等于$0$的，$x_{\text{test}}$只需要与支持向量做内积即可