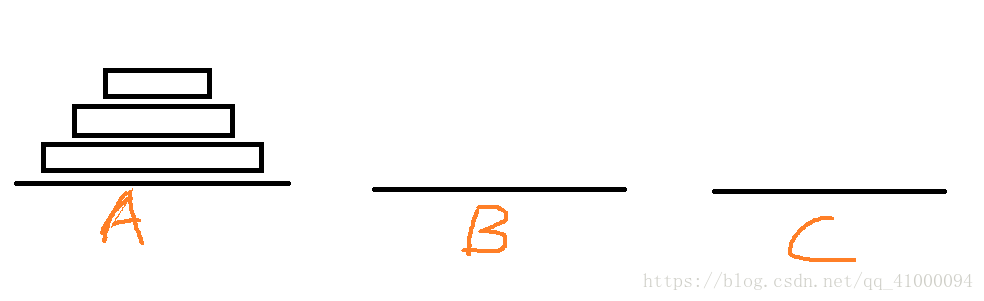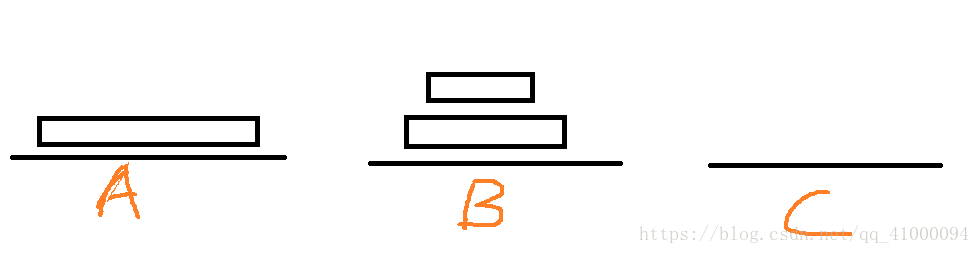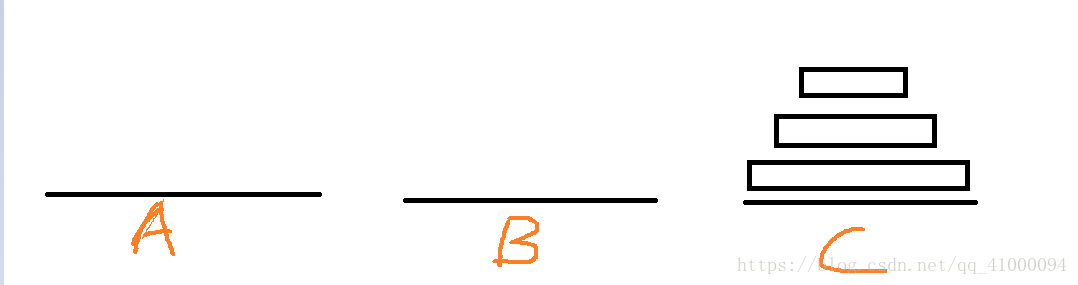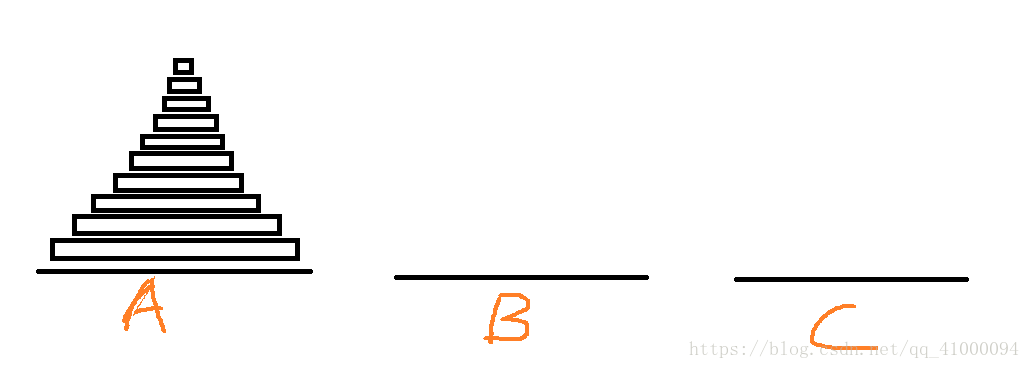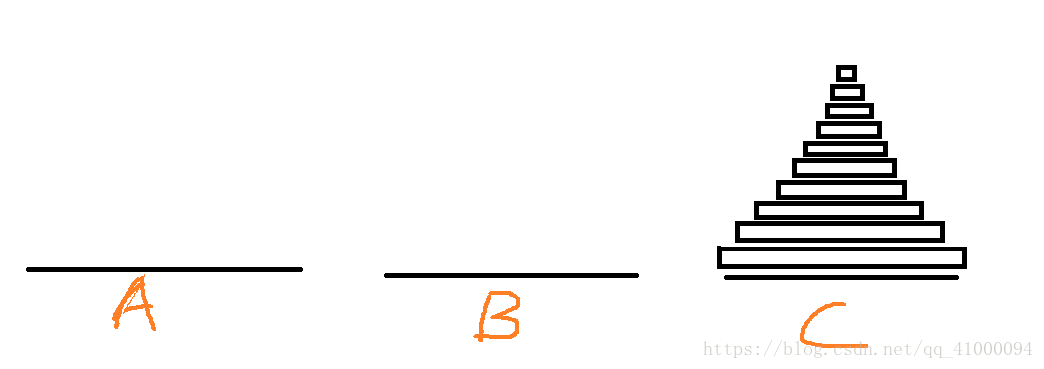关于汉诺塔的问题,代码很多人都知道,甚至倒背如流,但是真正能讲明原理的人却不多,下面我从几个角度来剖析一下这个经典递归问题。
首先描述一下问题
把A杆上的盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上
再把代码列出来
#include<stdio.h>
int index=1;
void move(char x,char y){
printf("第%d步:从%c移动到%c上.\n",index++,x,y);
}
void hanoi(int n, char X, char Y, char Z){
if(n!=0)
{
hanoi(n-1,X,Z,Y);
move(X,Z);
hanoi(n-1,Y,X,Z);
}
}
int main(){
int i;
scanf("%d",&i);
hanoi(i,'A','B','C');
}
此处i为要移动的塔个数。
下面开始分析整个问题,先从最简单的两个塔说起。
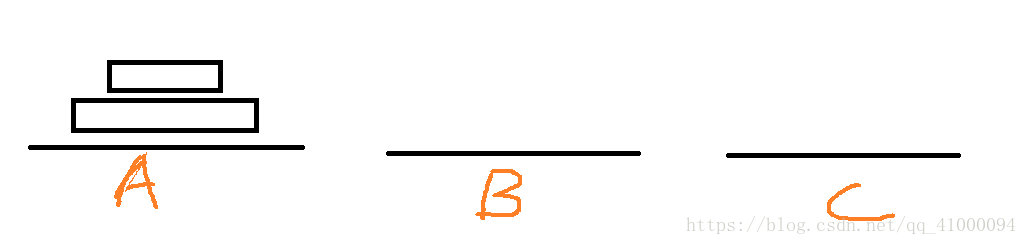
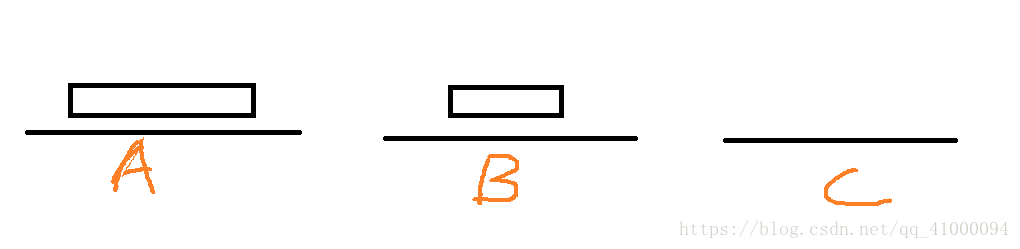
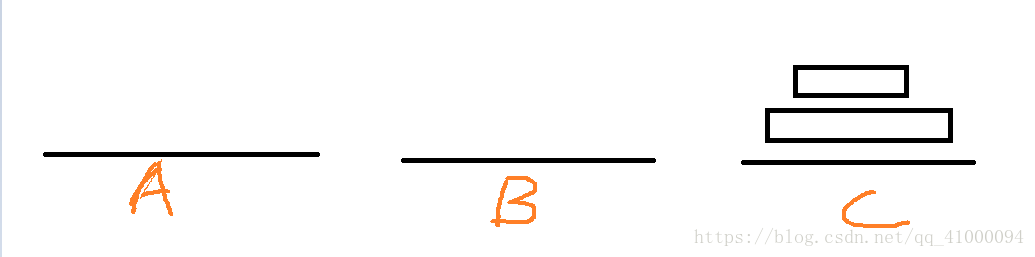
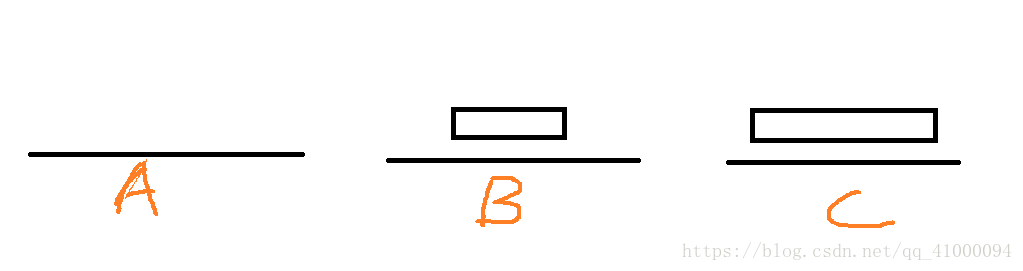
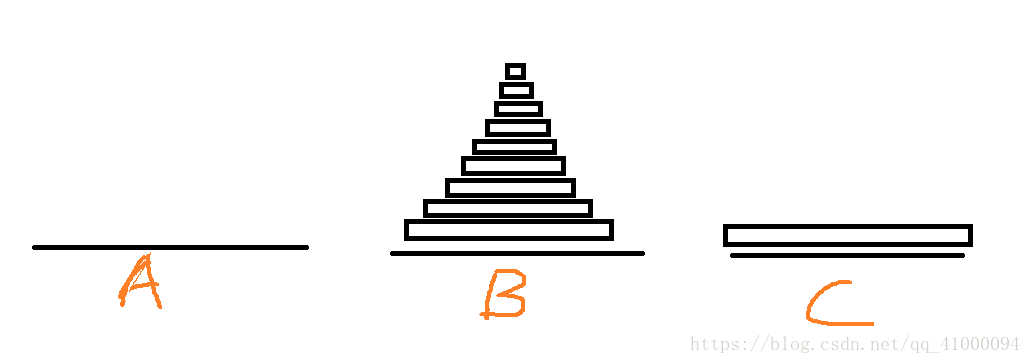
两个盘虽然简单,但多个盘的问题都是基本上围绕“两个盘”的问题组合而成的。所以理解两个塔的移动非常重要。根据这四张图,可以发现以下规律:
- 两个盘的移动可以在利用任一一个底座的辅助,移动到另一个底座上,在两个底座之间完成,不需要第三个底座的辅助(在此处是通过B塔的辅助移动到了C上)。
==============
接下来再画一个三个塔的图。
由双塔问题可知,A上面两个盘可通过C辅助移动到B上。
再把A上的最底的一层塔移动到C上。
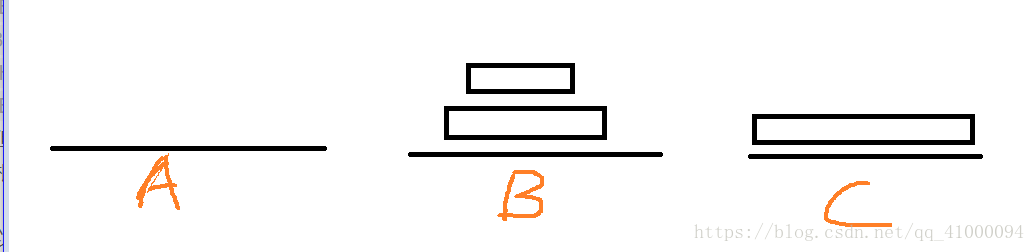
又由双塔问题可知,B上的两个塔可利用A辅助移动到C上(C的大小大于B上的两个塔,所以移动始终不受限制)。
也许你已经发现规律了,即每次都是先将其他盘移动到辅助底座上,并将最底下的盘移到C底座上,然后再把原先的底座作为辅助底座,并重复此过程。
===========
到现在,汉诺塔的问题就解决了一大半了。
现在开始分析代码实现,首先是递归的定义。
void hanoi(int n, char A, char B, char C)
直接的意思是,有n个盘,A,B,C三个底座,实际意思是,一共有n个盘,要从A底座移动到C底座上。其实最好的理解是,从A底座利用B底座辅助将n个盘移动到C底座上。
int index=1;
void move(char x,char y){
printf(“第%d步:从%c移动到%c上.\n”,index++,x,y); }
move为一个打印移动步骤的函数,在这里我定义了一个全局变量index来记录所进行的步骤数。
void hanoi(int n, char A, char B, char C){
if(n!=0)
{
hanoi(n-1,A,C,B);
move(A,C);
hanoi(n-1,B,A,C);
}
}核心代码的意图就是
1.首先将A底座上面的n-1个盘利用C底座的辅助,移动到B底座。(hanoi(n-1,A,C,B);)
2.再把A底座上最后最大的盘移动到C底座。(move(A,C);)
3.最后再把B底座上的盘利用A底座辅助移动到C底座(hanoi(n-1,B,A,C);)
此递归的结束条件为当n等于0时,表明已经移动完成。
有没有一种似曾相识的感觉,或许你已经发现规律了,其实n的塔的问题最终会转换为三塔双塔的问题,其原理是与三塔双塔问题相同的,在数量上有衍生罢了。