这就是GBDT算法原理

GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力（generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模型而引起大家关注。
GBDT是基于决策树，想学习关于决策树的内容可以看这篇文章https://blog.csdn.net/blank_tj/article/details/82081002

---

决策树分为两大类，回归树和分类树。前者用于预测实数值，如明天的温度、用户的年龄、网页的相关程度；后者用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。这里要强调的是，前者的结果加减是有意义的，如10岁+5岁-3岁=12岁，后者则无意义，如男+男+女=到底是男是女？ GBDT的核心在于累加所有树的结果作为最终结果，就像前面对年龄的累加（-3是加负3），而分类树的结果显然是没办法累加的，所以GBDT中的树都是回归树，不是分类树，这点对理解GBDT相当重要（尽管GBDT调整后也可用于分类但不代表GBDT的树是分类树）。

回归树总体流程是在每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差：即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和 除以 N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。

加法模型

GBDT算法可以看成是由K棵树组成的加法模型：

$\hat{y}_i = \sum^K_{k=1}f_k(x_i),f_k \in F\quad\quad\quad(1)$

其中$F$为所有树组成的函数空间，以回归任务为例，回归树可以看作为一个把特征向量映射为某个score的函数。该模型的参数为：$\Theta = {f_1,f_2,..,f_K}$。于一般的机器学习算法不同的是，加法模型不是学习d维空间中的权重，而是直接学习函数（决策树）集合。上述加法模型的目标函数定义为：

$Obj = \sum^n_{i=1}\ l(y_i,\hat{y}_i) + \sum^K_{k=1}\Omega(f_k)$

其中 $\Omega$ 表示决策树的复杂度，那么该如何定义树的复杂度呢？比如，可以考虑树的节点数量、树的深度或者叶子节点所对应的分数的$L2$范数等等。

如何来学习加法模型呢？

解这一优化问题，可以用前向分布算法（forward stagewise algorithm）。因为学习的是加法模型，如果能够从前往后，每一步只学习一个基函数及其系数（结构），逐步逼近优化目标函数，那么就可以简化复杂度。这一学习过程称之为Boosting。具体地，我们从一个常量预测开始，每次学习一个新的函数，过程如下：

$\hat{y}^0_i = 0\\\hat{y}^1_i = f_1(x_i) = \hat{y}^0_i = f_1(x_i)\\\hat{y}^2_i = f_1(x_i) + f_2(x_i) = \hat{y}^1_i+f_2(x_i)\\...\\\hat{y}^t_i = \sum^t_{k=1}f_k(x_i) = \hat{y}^{t-1}_i + f_t(x_i)$

那么，在每一步如何决定哪一个函数 $f$ 被加入呢？指导原则还是最小化目标函数。
在第$t$步，模型对$x_i$的预测为：$\hat{y}^t_i = \hat{y}^{t-1}_i + f_t(x_i)$，其中$f_t(x_i)$为这一轮我们要学习的函数（决策树）。这个时候目标函数可以写为：

$Obj^{(t)} = \sum^n_{t=1}\ l(y_i,\hat{y}^t_i) + \sum^t_{i=i}\Omega(f_i)\\ \quad\quad\ \ \ =\sum^n_{i=1} l(y_i, \hat{y}^{t-1}_i + f_t(x_i)) + \Omega(f_t) + constant \quad\quad\quad (1)$

举例说明，假设损失函数为平方损失（square loss），则目标函数为：
$Obj^{(t)} = \sum^n_{i=1}(y_i - (\hat{y}^{t-1}_i +f_t(x_i)))^2 + \Omega(f_t) + constant \\ \quad\quad\ \ =\sum^n_{i=1}[2(\hat{y}^{t-1}_i - y_i)f_t(x_i) + f_t(x_i)^2]+\Omega(f_t) + constant \quad\quad\quad(2)$

其中，$(\hat{y}^{t-1}_i - y_i)$称之为残差$(residual)$。因此，使用平方损失函数时，GBDT算法的每一步在生成决策树时只需要拟合前面的模型的残差。

泰勒公式

设n是一个正整数，如果定义在一个包含$\alpha$的区间上的函数$f$在$\alpha$点处n+1次可导，那么对于这个区间上的任意x都有：$f(x) = \sum^N_{n=0} \frac{f^{n}(\alpha)}{n!}(x-\alpha)^n +R_n(x)$，其中的多项式称为函数在$\alpha$处的泰勒展开式，$R_n(x)$是泰勒公式的余项且是$(x-\alpha)^n$的高阶无穷小。

根据泰勒公式把函数$f(x + \Delta x) \approx f(x) + f^{'}(x) \Delta x + \frac{1}{2}f^{''}(x)\Delta x^2 \quad\quad\quad(3)$

由等式(1)可知，目标函数是关于变量$\hat{y}^{t-1}_i + f_t(x_i)$的函数，若把变量$\hat{y}_i^{t-1}$看成是等式(3)中的$x$，把变量$f_t(x_i)$看成是等式(3)中的$\Delta x$，则等式(1)可转化为：

$Obj^{(t)} = \sum^n_{i=1}[l(y_i,\hat{y}^{t-1}_i) + g_if_t(x_i) + \frac{1}{2}h_if^2_t(x_i)] + \Omega(f_t) + constant \quad\quad\quad (4)$

其中，$g_i$定义为损失函数的一阶导数，即$g_i = \partial_{\hat{y}^{t-1}}l(y_i,\hat{y}^{t-1})；$$h_i$定义为损失函数的二阶导数，即$h_i = \partial^2_{\hat{y}^{t-1}}l(y_i,\hat{y}^{t-1})$。

假设损失函数为平方损失函数，则$g_i = \partial _{\hat{y}^{t-1}}(\hat{y}^{t-1} - y_i)^2 = 2(\hat{y}^{t-1} - y_i)，h_i = \partial^2_{\hat{y}^{t-1}}(\hat{y}^{t-1} - y_i)^2 = 2$，把$g_i$和$h_i$带入等式（4）和（2）。

由于函数中的常量在函数最小化的过程中不起作用，因此我们可以从等式(4)中移除掉常量项，得：

$Obj^{(t)} \approx \sum^n_{i=1}[g_if_t(x_i) + \frac{1}{2}h_if^2_t(x_i)] + \Omega(f_t)\quad\quad\quad(5)$

由于要学习的函数仅仅依赖于目标函数，从等式(5)可以看出只需为学习任务定义好损失函数，并为每个训练样本计算出损失函数的一阶导数和二阶导数，通过在训练样本集上最小化等式(5)即可求得每步要学习的函数$f(x)$，从而根据加法模型等式(0)可得最终要学习的模型。

GBDT算法

一颗生成好的决策树，假设其叶子节点个数为$T$，该决策树是由所有叶子节点对应的值组成的向量$w \in R^T$，以及一个把特征向量映射到叶子节点索引$(Index)$的函数$q:R^d \rightarrow {1,2,⋯,T}$组成的。因此，决策树可以定义为$f_t(x)=w_{q(x)}$。

决策树的复杂度可以由正则项 $\Omega (f_t) = \gamma T + \frac{1}{2}\lambda\sum^T_{j=1}w^2_j$ 来定义，即决策树模型的复杂度由生成的树的叶子节点数量和叶子节点对应的值向量的L2范数决定。
定义集合$I_j=${$i|q(x_i)=j \ $}为所有被划分到叶子节点j的训练样本的集合。等式(5)可以根据树的叶子节点重新组织为$T$个独立的二次函数的和：

$Obj^{(t)} \approx \sum^n_{i=1}[g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i)] + \Omega(f_t)\\ \quad\quad\ \ = \sum^n_{i=1}[g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i)] + \gamma T + \frac{1}{2}\lambda \sum^T_{j=1}\omega^2_j \\ \quad\quad \ \ =\sum^T_{j=1}[(\sum_{i \in I_j} g_i)\omega_j + \frac{1}{2}(\sum_{i \in I_j}h_i + \lambda)\omega^2_j] + \gamma T\quad\quad\quad(6)$

定义$G_j = \sum_{i \in I_j}g_i， H_j = \sum_{i \in I_j}h_i$，则等式$(6)$可写为：

$Obj^{(t)} = \sum^T_{j=1}[G_i\omega_j +\frac{1}{2}(H_i + \lambda)\omega^2_j] + \gamma T$

假设树的结构是固定的，即函数$q(x)$确定，令函数$Obj^{(t)}$的一阶导数等于0，即可求得叶子节点j对应的值为：

$\omega^*_j = - \frac{G_j}{H_j + \lambda}\quad\quad\quad(7)$

此时，目标函数的值为：

$Obj = -\frac{1}{2}\sum^T_{j=1}\frac{G^2_j}{H_j + \lambda} + \gamma T\quad\quad\quad(8)$

综上，为了便于理解，单颗决策树的学习过程可以大致描述为：

1)枚举所有可能的树结构$q$。
2)用等式(8)为每个$q$计算其对应的分数$Obj$，分数越小说明对应的树结构越好。
3)根据上一步的结果，找到最佳的树结构，用等式(7)为树的每个叶子节点计算预测值。

然而，可能的树结构数量是无穷的，所以实际上我们不可能枚举所有可能的树结构。通常情况下，我们采用贪心策略来生成决策树的每个节点。

1)从深度为0的树开始，对每个叶节点枚举所有的可用特征。
2)针对每个特征，把属于该节点的训练样本根据该特征值升序排列，通过线性扫描的方式来决定该特征的最佳分裂点，并记录该特征的最大收益（采用最佳分裂点时的收益）。
3)选择收益最大的特征作为分裂特征，用该特征的最佳分裂点作为分裂位置，把该节点生长出左右两个新的叶节点，并为每个新节点关联对应的样本集。
4)回到第1步，递归执行到满足特定条件为止。

如何计算每次分裂的收益呢？假设当前节点记为$C$，分裂之后左孩子节点记为$L$，右孩子节点记为$R$，则该分裂获得的收益定义为当前节点的目标函数值减去左右两个孩子节点的目标函数值之和：$Gain=Obj_C−Obj_L−Obj_R$，具体地，根据等式(8)可得：

$Gain = \frac{1}{2}[\frac{G^2_L}{H_L + \lambda} + \frac{G^2_R}{H_R + \lambda} - \frac{{(G_L + G_R)}^2}{H_L + H_R + \lambda}] - \gamma$

其中，−$\gamma$项表示因为增加了树的复杂性（该分裂增加了一个叶子节点）带来的惩罚。

---

总结一下GBDT算法

1)算法每次迭代生成一颗新的决策树

2)在每次迭代开始之前，计算损失函数在每个训练样本点的一阶导数$g_i$和二阶导数$h_i$

3)通过贪心策略生成新的决策树，通过等式(7)计算每个叶节点对应的预测值

4)把新生成的决策树$f_t(x)$添加到模型中：$y^t_i=y^{t−1}_i+f_t(x_i)$

通常在第四步，我们把模型更新公式替换为：$y^t_i=y^{t−1}_i+\epsilon f_t(x_i)$，其中$\epsilon$称之为步长或者学习率。增加$\epsilon$因子的目的是为了避免模型过拟合。

---

机器学习算法的目的

GBDT算法是一种监督学习算法。监督学习算法需要解决如下两个问题：

$Obj(\Theta) = L(\Theta) + \Omega(\Theta)$

$L(\Theta)$：是损失函数，损失函数尽可能的小，这样使得目标函数能够尽可能的符合样本。
$\Omega(\Theta)$：是正则化函数， 正则化函数对训练结果进行惩罚，避免过拟合，这样在预测的时候才能够更准确。

目标函数之所以定义为损失函数和正则项两部分，是为了尽可能平衡模型的偏差和方差(Bias Variance Trade-off)。
机器学习算法需要最终学习到损失函数尽可能小并且有效的防止过拟合。
以样本随时间变化对某件事情发生的变化为例，如下几副图形象的说明了机器学习的作用。
假设随着时间的变化对K话题存在如下样本：

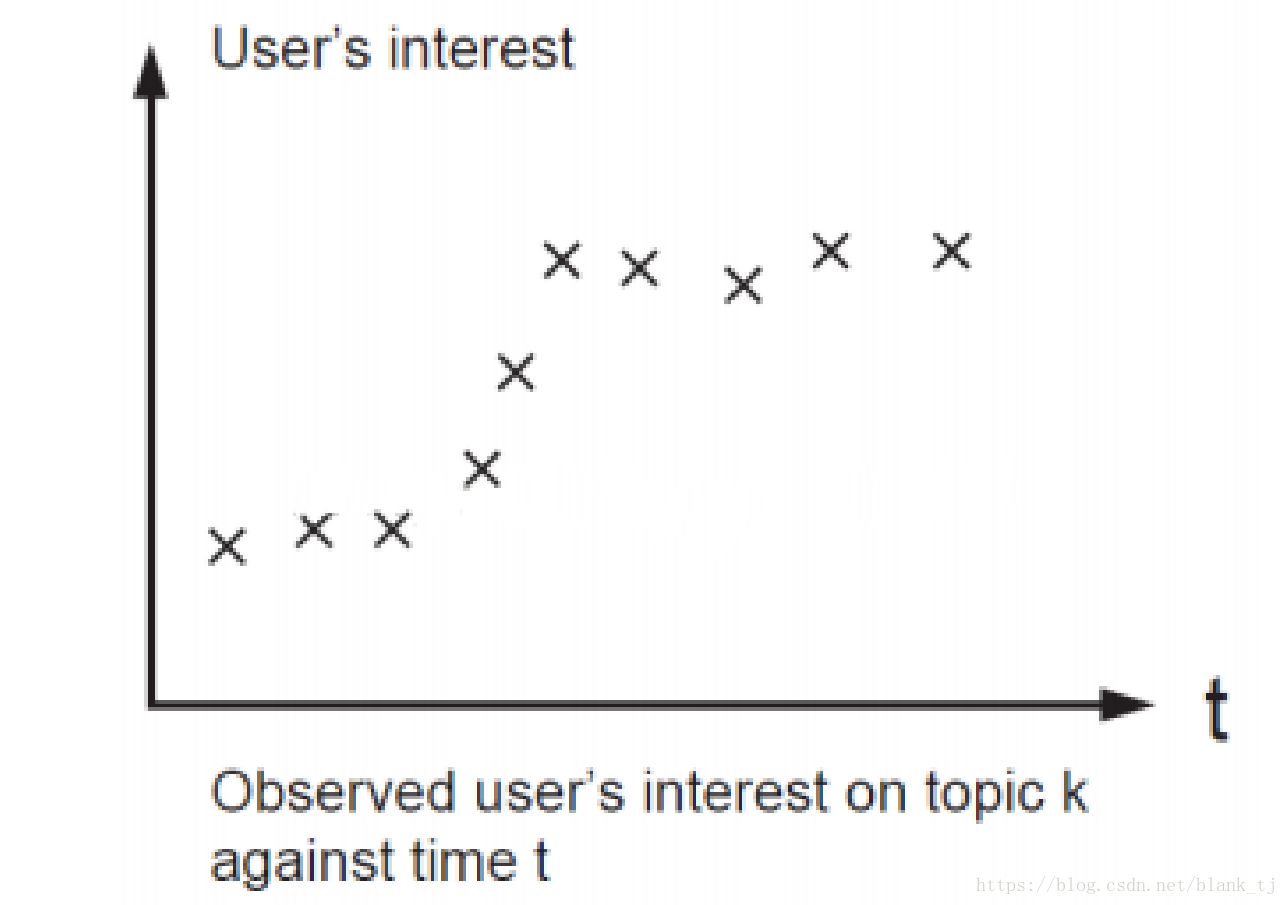
如果没有有效的正则化，则学习结果会如下图所示：

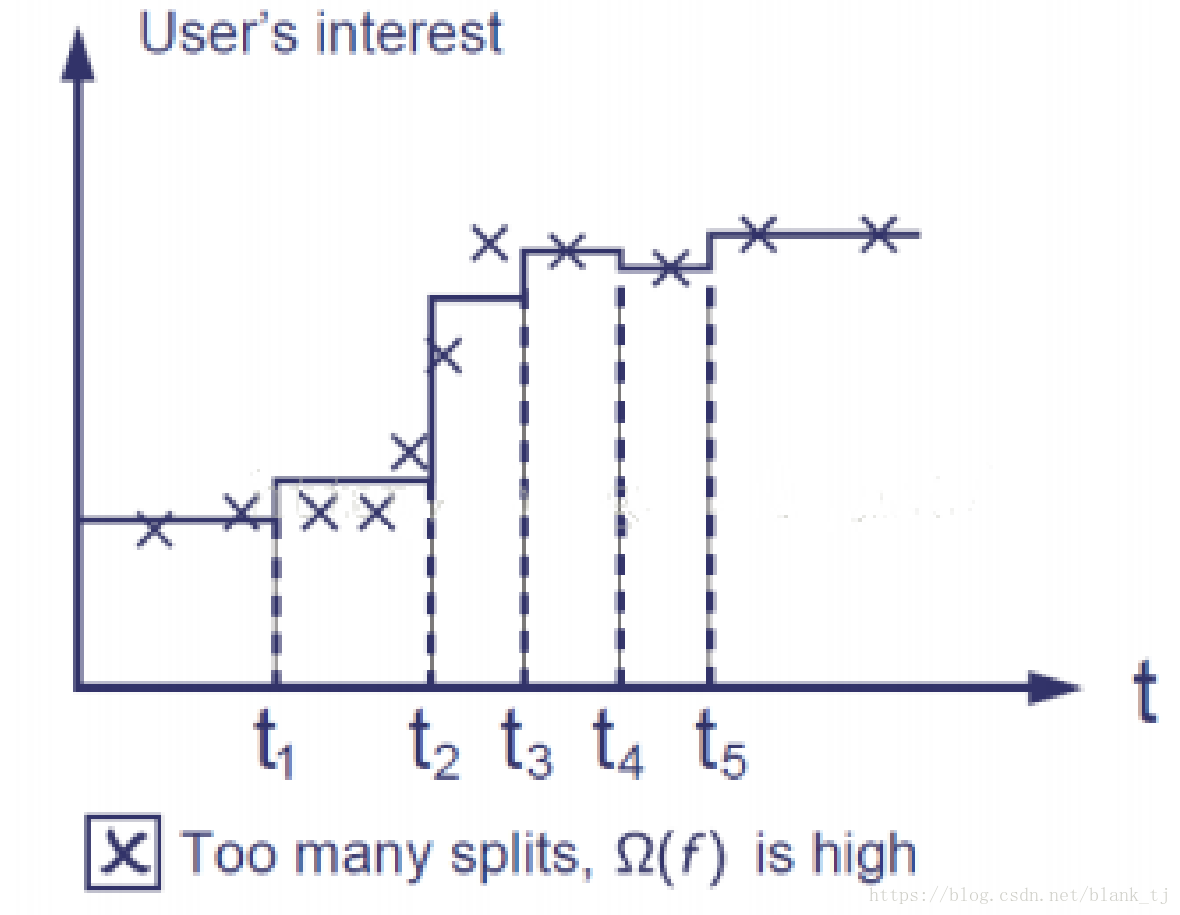
这种情况下，学习结果跟样本非常符合，损失函数也非常小，但是这种样本在预测的时候，由于过拟合，失败率会很高。
如果损失函数太大，则学习结果如下图所示：

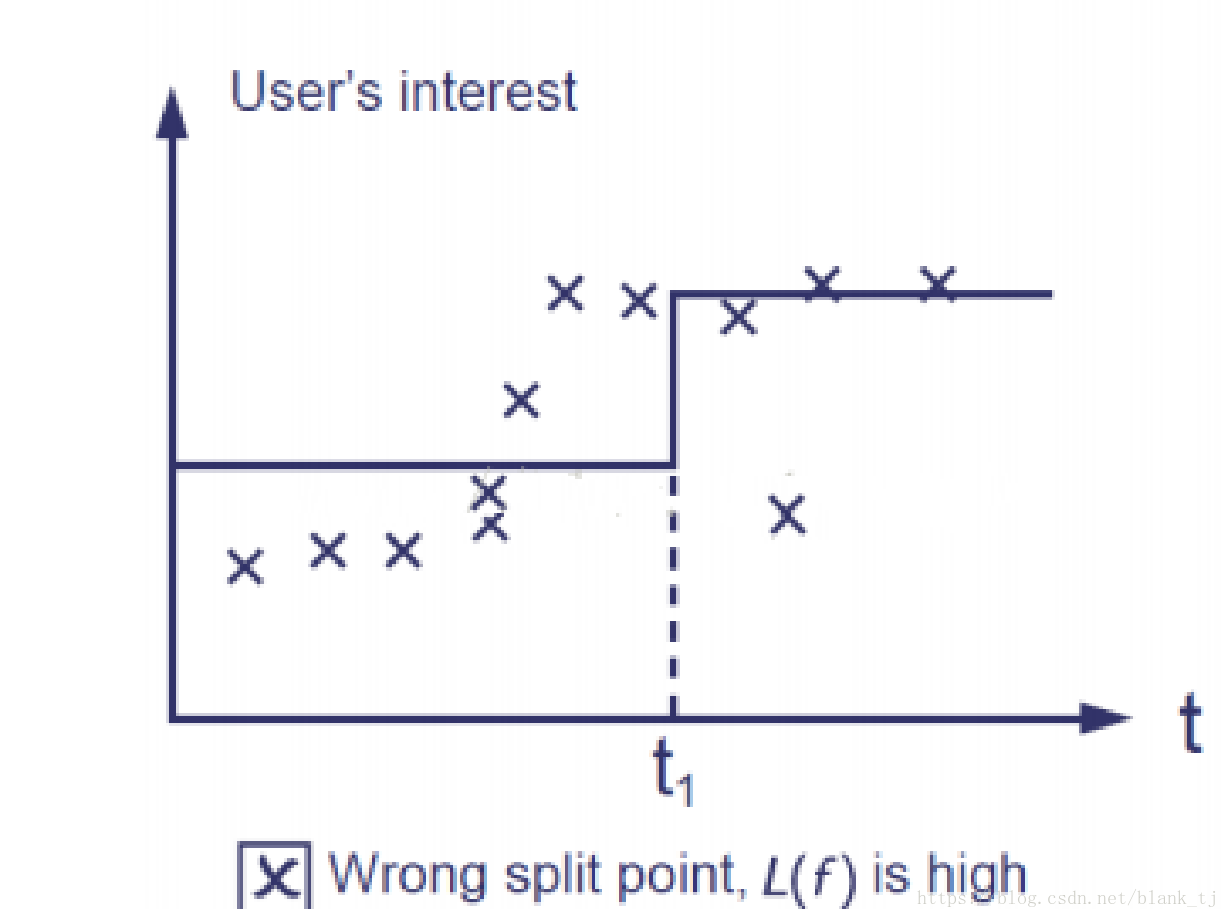
这种情况，学习结果跟样本差别太大，损失函数也很大，在预测的时候由于误差跳大，失败率也会很高。
损失函数和正则化防止过拟合平衡后的学习结果如下图所示：

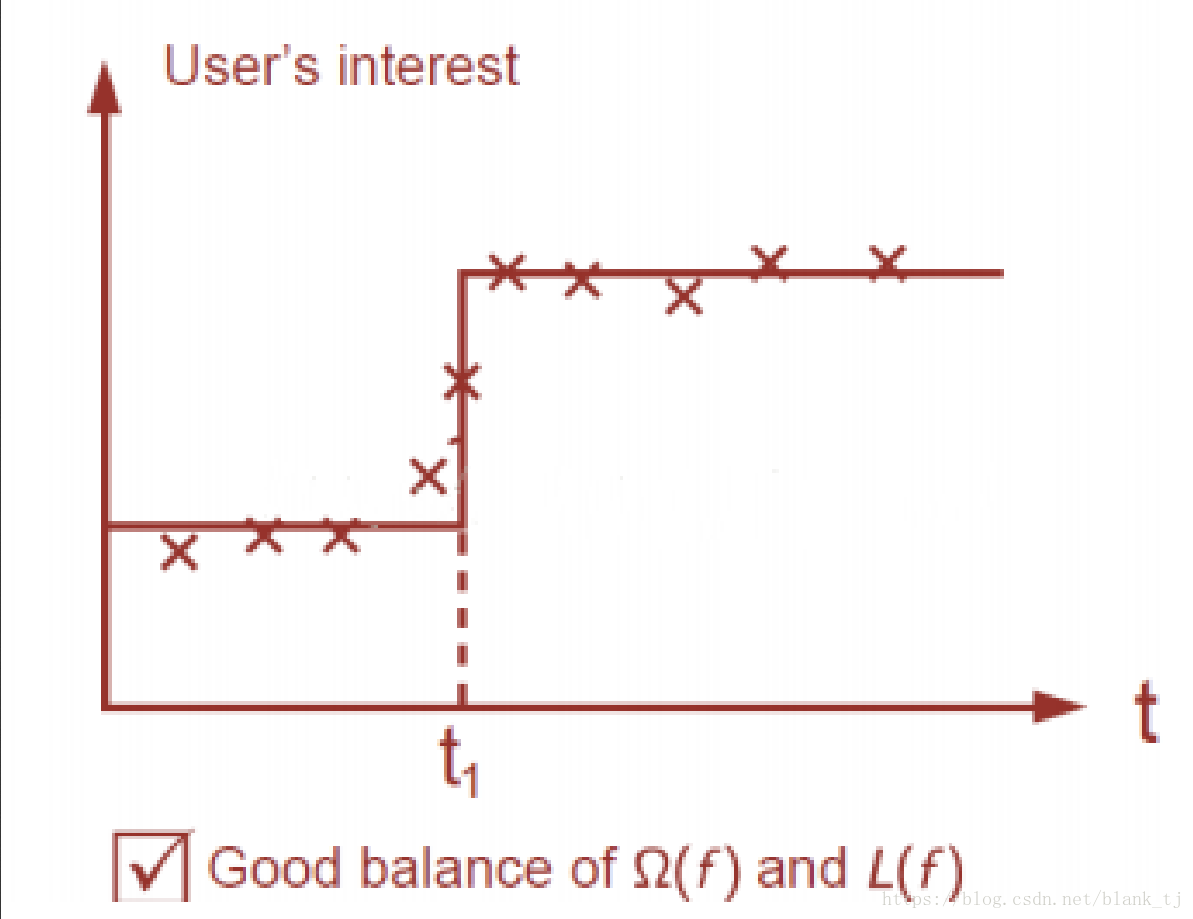
在这种情况下损失函数和正则化函数防止过拟合达到了一个平衡，预测会比较准。

---

参考了一篇非常不错的文章：https://www.cnblogs.com/yangxudong/p/6220485.html