银行信用评分卡中的WOE在干什么？

woe全称叫Weight of Evidence，常用在风险评估、授信评分卡等领域。

IV全称是Information value，可通过woe加权求和得到，衡量自变量对应变量的预测能力。

虽然网上到处都是神经网络、xgboost的文章，但当下的建模过程中（至少在金融风控领域）并没有完全摆脱logistic模型，原因大致有以下几点：

logistic模型客群变化的敏感度不如其他高复杂度模型，因此稳健更好，鲁棒性更强。
模型直观。系数含义好阐述、易理解。对金融领域高管以及银行出身的建模专家，变量系数可以跟他们的业内知识做交叉验证，更容易让人信服。
也是基于2的模型直观性，当模型效果衰减的时候，logistic模型能更好的诊断病因。

IV值我相信相关领域的人都用过，所以本文不展开讲。

本文主要讲的是WOE具有什么意义，或者说我们能从WOE中获得什么信息。

-------------------------------------本文目录-------------------------------------

一、 WOE的意义

二、如何计算WOE

三、 WOE的单调性

---1. WOE做差（引入）

---2. Odds Ratio

扫描二维码关注公众号，回复： 2933115 查看本文章

----------a. OR的计算

----------b. OR在逻辑回归中的意义

----------c. OR的估计值与WOE

---3. 回到正题（WOE单调意义）

四、 WOE呈线性&WOE编码的意义

五、浅谈WOE与贝叶斯

一、先总结WOE的意义（这样才有看下去的动力

计算woe（以及IV）的意义我所知的有以下几点：

IV值可以衡量各变量对y的预测能力，用于筛选变量。
对离散型变量，woe可以观察各个level间的跳转对odds的提升是否呈线性，而IV可以衡量变量整体（而不是每个level）的预测能力。

当你有千级别或者万级别的字段时，建模前计算IV值是很有必要的。以地区邮编为例，level很多，每个level下样本少，常规的处理是用dummy encoding将n个level的变量拆成n-1个哑变量，然后建模做检验，得到这n-1个哑变量的显著性，再对n-1个哑变量做聚类等处理才能feed in model。如果到最后你不管怎么处理都不太好feed进model，那就白忙了，场面会相当的尴尬。这个时候就体现了事先计算IV值来筛选变量的重要性了。

对连续型变量，woe和IV值为分箱的合理性提供了一定的依据。

分箱处理连续型变量会有信息损失，但由于绝大多数情况下连续型变量对odds的提升都不是线性的，这里能产生的负面影响远比信息损失要大，因此一般都需要做分箱处理。

用woe编码可以处理缺失值问题。
欢迎补充

二、如何计算WOE

以信用评分卡的建模场景为例：X是客户样本字段，Y表示客户逾期与否，其中Y=1代表逾期，Y=0代表未逾期。我们希望能用客户已知的信息来预测客户借款后发生逾期的概率，以此来决定是否放贷。

下面我们拿Age(年龄)这个变量来计算相关的woe ，首先对每个level分层统计【表1】：

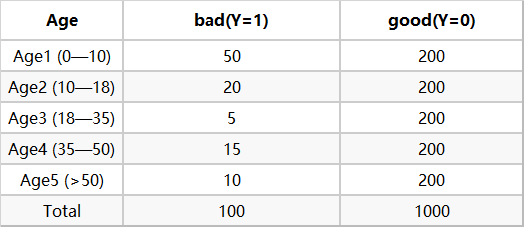
然后计算各分层的好坏占比【表2】

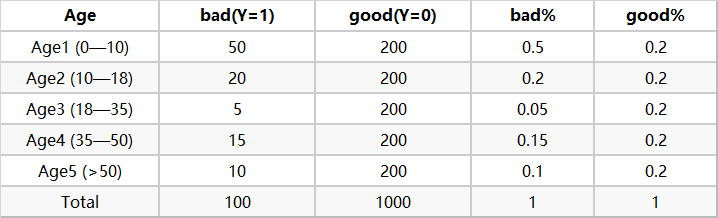
最后通过好坏占比计算woe【表3】

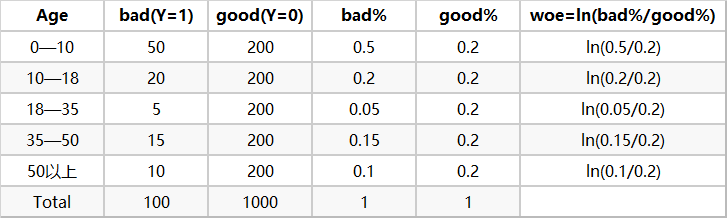
以上三个表就是计算woe的过程，简单易懂。

接下来我们讲讲woe该怎么用以及有什么意义。

三、WOE的单调性（涉及odds ratio）

3.1 WOE做差是什么？

当我们算完woe的时候，我们关注的点一般会有这几个：woe是否单调、woe是否呈线性、以及IV值的大小。这里讲一下单调和线性的意义，主要跟logistic回归中的odds ratio相关。

刚接触woe的时候，为了研究它的单调性是什么，我尝试着将WOE做差，发现得到的结果跟Odds Ratio的形式很像，都是列联表交叉乘做商：

$\begin{equation} \begin{aligned} WOE_{Age_{1}}-WOE_{Age_{2}}&=ln(\frac{Bad\%_{Age_{1}}}{Good\%_{Age_{1}}})-ln(\frac{Bad\%_{Age_{2}}}{Good\%_{Age_{2}}})\\ &=ln(\frac{Bad\%_{Age_{1}}}{Bad\%_{Age_{2}}}*\frac{Good\%_{Age_{2}}}{Good\%_{Age_{1}}})\\ &=ln(\frac{\#Bad_{Age_{1}}}{\#Bad_{Age_{2}}}*\frac{\#Good_{Age_{2}}}{\#Good_{Age_{1}}}) \end{aligned} \end{equation}$

3.2 Odds Ratio（OR）

为了了解WOE，这里分三步简单讲一下Odds Ratio（优势比）。

a. OR的计算

首先要知道Odds（优势），指的是事件发生和不发生的比例，即：

$Odds=\frac{p}{1-p}$

下面我们设定这个事件为客户逾期，即Y=1。那么 $Age=Age_{1}$ 时的Odds为：

$\begin{equation} \begin{aligned} Odds_{Age_{1}}&=\frac{P(Y=1|Age=Age_{1})}{P(Y=0|Age=Age_{1})}\\ \end{aligned} \end{equation}$

而Odds Ratio则是两组odds的比值，比如 $Age_{1}$ 和 $Age_{2}$ 之间的Odds Ratio为：

$\begin{equation} \begin{aligned} OR_{Age2/Age1}&=\frac{Odds_{Age_{2}}}{Odds_{Age_{1}}}\\ &=\frac{P(Y=1|Age=Age_{2})/P(Y=0|Age=Age_{2})}{P(Y=1|Age=Age_{1})/P(Y=0|Age=Age_{1})} \\ \end{aligned} \end{equation}$

b. OR在逻辑回归中的意义

Odds和Odds ratio在logistic中非常值得重视，因为他们跟参数的interpretation密切相关。

在logistic回归中：

$\begin{equation} \begin{aligned} ln\frac{p}{1-p}&=\beta_{0}x_{0}+\beta_{1}x_{1}+...+\beta_{n}x_{n} \end{aligned} \end{equation}$

【OR的意义】当 $x_{i}$ 增加1个单位时，odds将变为原来的 $e^{a_{i}}$ 倍：

$\begin{equation} \begin{aligned} OR_{x_{i}+1/x_{i}}&=\frac{Odds_{2}}{Odds_{1}}=\frac{p_{1}/(1-p_{1})}{p_{2}/(1-p_{2})}\\ &=\frac{e^{\sum_{j\ne i}{\beta_{j}x_{j}}+\beta_{i}(x_{i}+1)}}{e^{\sum_{j\ne i}{\beta_{j}x_{j}}+\beta_{i}x_{i}}}\\ &=e^{\beta_{i}} \end{aligned} \end{equation}$

OR在logistic中的意义在上面讲完了，下面来讲下OR是怎么和WOE联系起来的。

c. OR的估计值（Marginal OR）与WOE

一般的，我们可以通过列联表计算Odds和Odds Ratio的估计值。

【值得注意的是】通过列联表算得的 $\widehat{OR}$ 是指Marginal OR，大家可以将Marginal OR理解为模型 $y\sim x_{i}$ 的 $e^{\beta_{i}}$ ，这是个单变量回归模型。本文中涉及WOE的OR指的都是Marginal OR。而多元回归中的 $e^{\beta_{i}}$ 对应的是Conditional OR。两者是不一样的。

$\begin{equation} \begin{aligned} \widehat{Odds_{Age_{1}}}&=\frac{\#(Y=1)_{Age_{1}}}{\#(Y=0)_{Age_{1}}} =\frac{\#Bad_{Age_{1}}}{\#Good_{Age_{1}}}\\ \widehat{OR_{Age_{2}/Age_{1}}}&=\frac{\widehat{Odds_{Age_{2}}}}{\widehat{Odds_{Age_{1}}}}\\ &=\frac{\#Bad_{Age_{2}}}{\#Bad_{Age_{1}}}*\frac{\#Good_{Age_{1}}}{\#Good_{Age_{2}}} \\ ln(\widehat{OR_{Age_{2}/Age_{1}}})&=WOE_{Age_{1}}-WOE_{Age_{2}}\\ &=\beta \quad in \quad Y\sim Age， Age\in \{Age_{1},Age_{2} \} \end{aligned} \end{equation}$

3.3 回到正题

结合上面OR的知识，WOE单调实际上就意味着当 $Age_{i}$ 从 $Age_{1} \rightarrow Age_{2} \rightarrow Age_{3}\rightarrow Age_{4}\rightarrow Age_{5}$ 单调上升时，相应的 $Odds_{Age_{i}}$ 也呈现单调递增（递减）， $P(Y=1|Age_{i})$ 也呈单调递增（递减）。

我们可以用一个更简洁的公式概括上面的计算过程：

$\underbrace{ln\frac{P(Y=1|Age_{i})}{P(Y=0|Age_{i})}}_{ln(Odds_{Age_{i}})} =\underbrace{ln\frac{P(Y=1)}{P(Y=0)}}_{sample\_odds(常数)}+\underbrace{ln\frac{P(Age_{i}|Y=1)}{P(Age_{i}|Y=0)}}_{WOE_{Age_{i}}}$

从上式可以看出， $ln(Odds_{Age_{i}})$ 和 $WOE_{Age_{i}}$ 只差了一个常数。也就是说 $WOE_{Age_{i}}$ 越大， $P(Y=1|Age_{i})$ 越大。

#----------------------证明WOE之差与OR相等--------------------
import pandas as pd
import numpy as np
df=pd.DataFrame({'X1':np.random.randint(3,size=1000),\
                 'y':np.random.randint(2,size=1000)})
table=pd.crosstab(df['y'],df['X1'])
# 计算WOE差值
woe_table=table.div(table.sum(axis=1),axis=0)
woe=(woe_table.iloc[1,:]/woe_table.iloc[0,:]).apply(lambda x:np.log(x))
woe[1]-woe[0],woe[2]-woe[1]
# 计算OR
OR_0_1=np.log(1.0*table.iloc[0,0]*table.iloc[1,1]/table.iloc[0,1]/table.iloc[1,0])
OR_1_2=np.log(1.0*table.iloc[0,1]*table.iloc[1,2]/table.iloc[0,2]/table.iloc[1,1])
OR_0_1,OR_1_2

四、WOE呈线性&WOE编码的意义

WOE呈线性是一个很强的条件，比单调要强得多。一般来说是不会这么巧出现线性的情况的，我之所以要提，是因为我们可以通过WOE编码人为地让它呈线性，这个后面再提。

先说WOE呈线性的意义

如果一个变量的不同level（假设各level分别以 0,1,2,3...进行编码）的WOE呈线性，说明该变量每增加一个单位，对Odds产生的影响是一样的。

还记得开篇提到的邮政编码的例子么？在那里我们需要对属性变量做dummy encoding，因为我们不能保证变量从任意 $level_{i}$ 跳转到 $level_{i+1}$ 时对Odds产生的影响都一样，所以不能用{0,1,2,3...}这样等间距的编码方式。

WOE编码的意义

而WOE近似于事先计算了变量各level的Marginal Odds，将对应的WOE取代属性变量的原始值{0,1,2,3...}，即使用WOE编码，可以使得该变量每增加一个单位，Odds就增加相同的值，参考下图。

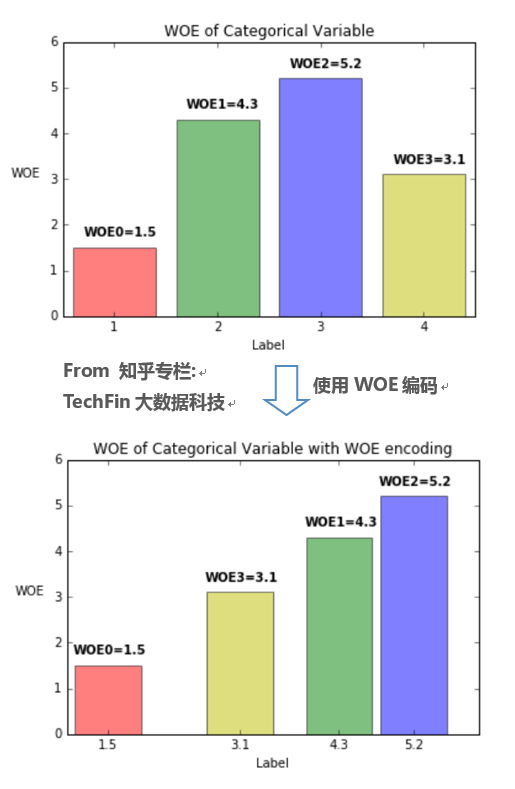
结论就是：如果使用了WOE编码，当我们对单变量进行回归（Y~Xi）时，可以不做dummy encoding，此时变量的系数恒为1。WOE编码起到了把回归系数“正则化”的作用。

代码提供验证：

from sklearn.linear_model import LogisticRegression   
import pandas as pd
import numpy as np
df=pd.DataFrame({'X1':np.random.randint(3,size=1000),\
                 'y':np.random.randint(2,size=1000)})
table=pd.crosstab(df['y'],df['X1'])
ratio_table=table.div(table.sum(axis=1),axis=0)
woe=ratio_table.iloc[1,:]/ratio_table.iloc[0,:]
# 使用WOE编码后，观察模型系数
df.X1=df.X1.replace({0:woe[0],1:woe[1],2:woe[2]})
glm=LogisticRegression(C=1e10)
glm.fit(df.loc[:,['X1']],df.y)
glm.coef_

五、浅谈WOE与贝叶斯

到收尾部分了，这里主要想说明一个问题：上面WOE解决的问题都是对单变量回归有效，在多元logistic回归里仍然有效么？

答案是无效的，多元logistic回归里的系数并不会因为WOE编码而全部等于1。

WOE也好，IV也好，做的都是单变量分析。我们认为对Y有较好预测能力的变量，在多元回归时仍然会有较好的预测能力。基于此逻辑可以用IV值来对变量的重要性进行排序。

WOE与贝叶斯因子的联系

简单提下贝叶斯因子，就不展开讲了，各位可以上网查Bayes factor。

$\underbrace{ln\frac{P(Y=1|Age_{i})}{P(Y=0|Age_{i})}}_{ln(Odds_{Age_{i}})} =\underbrace{ln\frac{P(Y=1)}{P(Y=0)}}_{sample\_odds(常数)}+\underbrace{ln\underbrace{\frac{P(Age_{i}|Y=1)}{P(Age_{i}|Y=0)}}_{Bayes\_Factor}}_{WOE_{Age_{i}}}$

当变量不止一个的时候，如果任意 $X_{i}$ 和 $X_{j}$ 关于 $Y$ 条件独立的话，则有：

$\begin{equation} \begin{aligned} ln\frac{P(Y=1|x_{1},x_{2},...,x_{k})}{P(Y=0|x_{1},x_{2},...,x_{k})} =ln\frac{P(Y=1)}{P(Y=0)}+ln\frac{P(x_{1},...,x_{k}|Y=1)}{P(x_{1},...,x_{k}|Y=0)}\\ \xlongequal[independent]{conditionally}ln\frac{P(Y=1)}{P(Y=0)}+\sum_{i=1}^{k}{ln\underbrace{\frac{P(x_{i}|Y=1)}{P(x_{i}|Y=0)}}_{Bayes\_Factor_{X_{i}}}} \end{aligned} \end{equation}$

条件独立经常跟贝叶斯相关的东西扯上关系，比如说朴素贝叶斯分类器，之所以“朴素”，就是因为各变量关于Y条件独立这一强假设。如果不满足条件独立，那么就会出现多个变量对结果产生协同影响的情况，极其影响结果。

为了弱化条件独立这一个强假设，出现了非完全朴素的贝叶斯分类器（semi-Bayes）

semi-Bayes 总体来说就是用各种规则来对变量进行加权（特别地，当权值是0/1的时候就是进行变量筛选了，并认为筛选后的变量条件独立），以此来抑制相关变量的协同影响。

我们将semi的思想用在上式，便有：

$\begin{equation} \begin{aligned} ln\frac{P(Y=1|x_{1},x_{2},...,x_{k})}{P(Y=0|x_{1},x_{2},...,x_{k})} \xlongequal[]{semi}ln\frac{P(Y=1)}{P(Y=0)}+\sum_{i=1}^{k}{\beta _{i} \underbrace{ln\underbrace{\frac{P(x_{i}|Y=1)}{P(x_{i}|Y=0)}}_{Bayes\_Factor_{X_{i}}}}_{WOE_{x_{i}}}} \end{aligned} \end{equation}$

这个就是用WOE编码后的logistic模型。

所以说WOE编码其实也可以从非完全条件独立的贝叶斯因子的角度去看待。

对WOE的介绍就到此结束了