学习资料:Principal Component Analysis
in 3 Simple Steps
简介
PCA算法的主要目标是识别数据的模式,发现变量之间的相关性。当变量之间相关性较强时,PCA算法降维的作用变得非常有意义了。总结下来就是:找到高维数据的最大协方差的方向,在保留大多数信息的情况下将其投影到低维子空间。
整个PCA过程貌似及其简单,就是求协方差的特征值和特征向量,然后做数据转换。
PCA与LDA
LDA的的目标是找到不同类别之间的区别,其在模式分类问题中比较有用。
PCA和数据降维
我们能计算出数据的特征向量,每个特征向量都有其对应的特征值,当有些特征值明显大于另一部分时,我们通过PCA法在只损失少量信息的情况下将数据降维到子空间的做法是合理的。
PCA的技术路线
- 标准化数据
- 计算协方差矩阵的特征值和特征向量,或执行奇异向量分解(SVD)
- 按照特征值排序找到前K个最大特征值对应的特征向量,K是新的特征子空间的维度
- 按照所选K个特征向量组建投影矩阵W
通过矩阵W将原始数据集X投影到K位特征子空间Y
其实PCA的本质就是对角化协方差矩阵。有必要解释下为什么将特征值按从大到小排序后再选。首先,要明白特征值表示的是什么?在线性代数里面我们求过无数次了,那么它具体有什么意义呢?对一个n∗n的对称矩阵进行分解,我们可以求出它的特征值和特征向量,就会产生n个n维的正交基,每个正交基会对应一个特征值。然后把矩阵投影到这n个基上,此时特征值的模就表示矩阵在该基的投影长度。特征值越大,说明矩阵(样本)在对应的特征向量上投影后的方差越大,样本点越离散,越容易区分,信息量也就越多。因此,特征值最大的对应的特征向量方向上所包含的信息量就越多,如果某几个特征值很小,那么就说明在该方向的信息量非常少,我们就可以删除小特征值对应方向的数据,只保留大特征值方向对应的数据,这样做以后数据量减小,但有用的信息量都保留下来了。PCA就是这个原理。
Iris数据集的准备
数据介绍
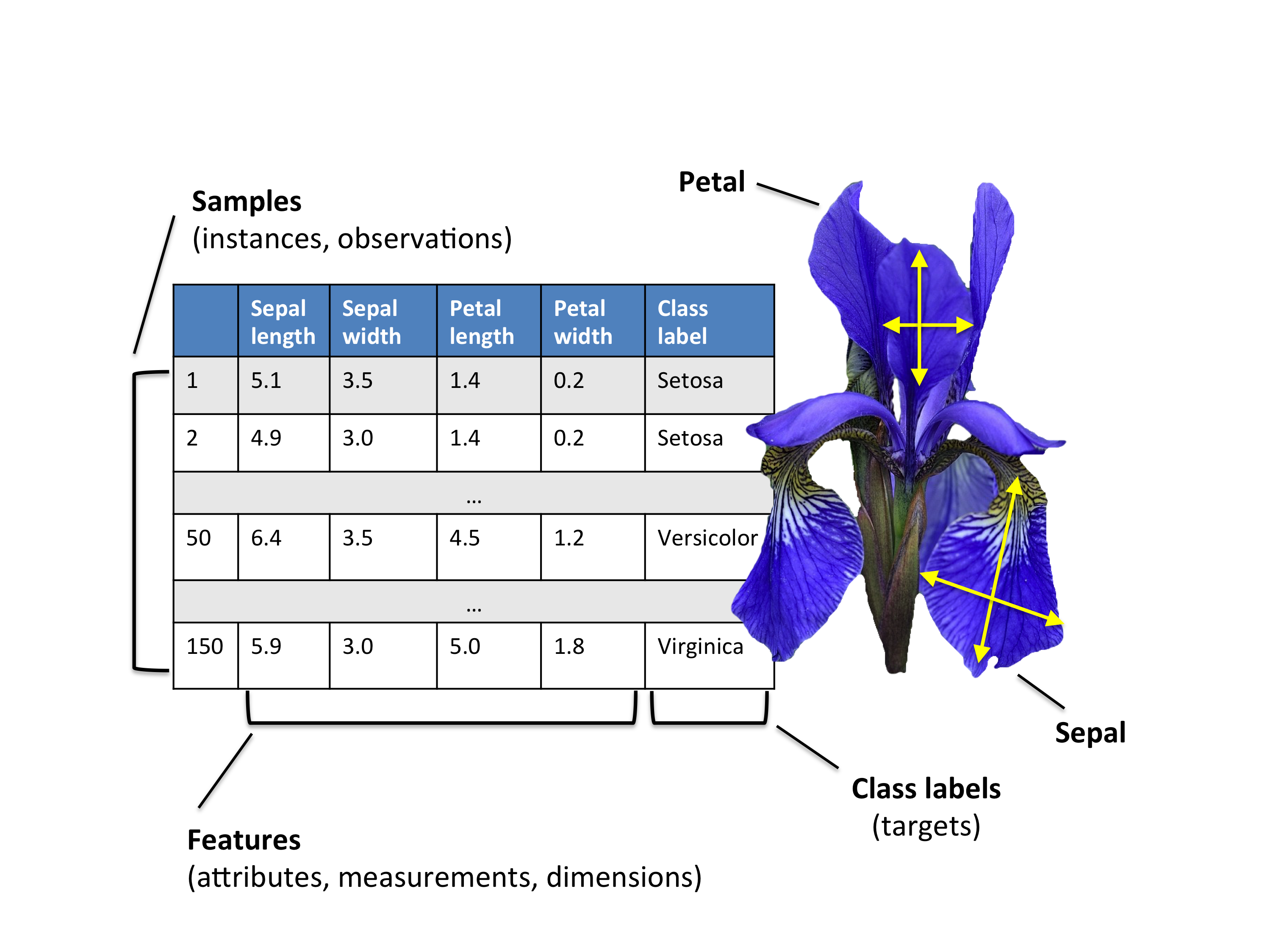
Iris数据集
数据集包含3种共150个鸢尾花图片
Iris-setosa (n=50)
Iris-versicolor (n=50)
Iris-virginica (n=50)
鸢尾花有四种特征 (cm)
1. 萼片长度
2. 萼片宽度
3. 花瓣长度
4. 花瓣宽度
加载数据集
利用pandas直接从UCI库加载数据集或从sklearn.datasets加载数据集
示例:http://www.cnblogs.com/Belter/p/8831216.html
数据标准化
根据原始特征的测算规模判断是否需要在使用PCA算法前对数据进行标准化,因为PCA会在保证轴向协方差最大的情况下产生相应的特征子空间,特比是在度量尺度不同的情况下,对数据进行标准化就变得格外重要。虽然Iris数据集中的特征都是以cm为单位,我们还是将数据转换为单位尺寸(均值为0,方差为1),这样处理能使很多机器学习算法有更好的表现。
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)
1-特征分解:计算特征值和特征向量
协方差矩阵的特征向量特征值代表了PCA的核心:
主成分的特征向量决定了新的特征空间的方向,特征值决定了它们的分量。
协方差矩阵
经典的PCA方法是通过协方差矩阵(d*d)的每一个元素表示两个向量之间的协方差,向量之间的协方差可以通过如下方法计算得到:

我们用一下公式概括计算
import numpy as np
mean_vec = np.mean(X_std, axis=0)
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
print('Covariance matrix \n%s' %cov_mat)
Covariance matrix
[[ 1.00671141 -0.11010327 0.87760486 0.82344326]
[-0.11010327 1.00671141 -0.42333835 -0.358937 ]
[ 0.87760486 -0.42333835 1.00671141 0.96921855]
[ 0.82344326 -0.358937 0.96921855 1.00671141]]我们也可以直接用Numpy的cov函数计算出协方差矩阵
print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))
NumPy covariance matrix:
[[ 1.00671141 -0.11010327 0.87760486 0.82344326]
[-0.11010327 1.00671141 -0.42333835 -0.358937 ]
[ 0.87760486 -0.42333835 1.00671141 0.96921855]
[ 0.82344326 -0.358937 0.96921855 1.00671141]]接下来我们可以在协方差矩阵的基础上做特征分解
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
print('Eigenvectors \n%s' %eig_vecs)
print('\nEigenvalues \n%s' %eig_vals)
Eigenvectors
[[ 0.52237162 -0.37231836 -0.72101681 0.26199559]
[-0.26335492 -0.92555649 0.24203288 -0.12413481]
[ 0.58125401 -0.02109478 0.14089226 -0.80115427]
[ 0.56561105 -0.06541577 0.6338014 0.52354627]]
Eigenvalues
[ 2.93035378 0.92740362 0.14834223 0.02074601]相关系数矩阵
当输入数据被标准化处理后,特征向量的协方差矩阵和相关矩阵是一样的,因为相关矩阵可以被理解为标准化后的协方差矩阵。
相关矩阵基础下的特征分解
cor_mat1 = np.corrcoef(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cor_mat1)
print('Eigenvectors \n%s' %eig_vecs)
print('\nEigenvalues \n%s' %eig_vals)
Eigenvectors
[[ 0.52237162 -0.37231836 -0.72101681 0.26199559]
[-0.26335492 -0.92555649 0.24203288 -0.12413481]
[ 0.58125401 -0.02109478 0.14089226 -0.80115427]
[ 0.56561105 -0.06541577 0.6338014 0.52354627]]
Eigenvalues
[ 2.91081808 0.92122093 0.14735328 0.02060771]我们可以清楚的发现三种方法德成风化的特征向量与对应的特征值是相同的:
- 标准化数据的协方差矩阵特征分解
- 相关矩阵的特征分解
- 标准化数据的相关矩阵特征分解
奇异向量分解(SVD)
虽然协方差或相关矩阵的特征分解可能更直观,但大多数PCA实现都执行一个奇异向量分解(SVD)来提高计算效率。因此,让我们执行一个SVD来确认结果确实是一样的:
SVD介绍:http://shartoo.github.io/SVD-decomponent/
u,s,v = np.linalg.svd(X_std.T)
u
u,s,v = np.linalg.svd(X_std.T)
u
2-选取主成分
排序特征对
PCA算法经典目标是将原始特征通过投影到小的子空间降维,特征向量组成轴。然而因为它们都是相同的单位长度1,特征向量只会定义新轴的方向。
for ev in eig_vecs:
np.testing.assert_array_almost_equal(1.0, np.linalg.norm(ev))
print('Everything ok!')
np.linalg.norm(ev)为求向量的范数
np.testing.assert_array_almost_equal()判断在允许精度内是否相等
Everything ok!特征值的大小反映了相应特征向量的所包含的信息量的大小,为了对数据进行降维,我们将特征对按照特征值的大小排序找到前K个特征向量。
# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)
# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in descending order:')
for i in eig_pairs:
print(i[0])
Eigenvalues in descending order:
2.91081808375
0.921220930707
0.147353278305
0.0206077072356可释方差
特征对排序后,新的问题是“我们需要为新的特征子空间选取多少个主成分”。
可释方差(Explained Variance)能够计算出主成分有多少信息。
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
with plt.style.context('seaborn-whitegrid'):
plt.figure(figsize=(6, 4))
plt.bar(range(4), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
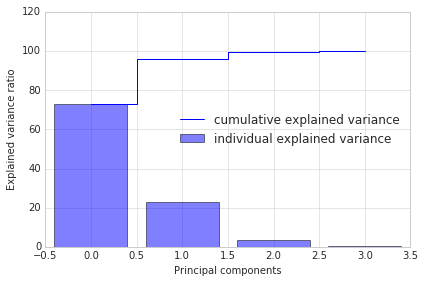
上图表明,72.77%的信息能被第一主成分代表,第二主成分为23.03%。第一和第二主成分共占95.8%。第三成分能够被舍弃掉而不会损失多少信息。
矩阵投影
我们根据特征值大小找出K个特征向量组建新的特征子空间,求出特征矩阵W。
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
eig_pairs[1][1].reshape(4,1)))
#np.hstack()将栈水平排列
print('Matrix W:\n', matrix_w)
Matrix W:
[[ 0.52237162 -0.37231836]
[-0.26335492 -0.92555649]
[ 0.58125401 -0.02109478]
[ 0.56561105 -0.06541577]]3-投影到新的特征空间
Y=X×W, 求出Y是我们转换后的样本数据。
Y = X_std.dot(matrix_w)
with plt.style.context('seaborn-whitegrid'):
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(Y[y==lab, 0],
Y[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()
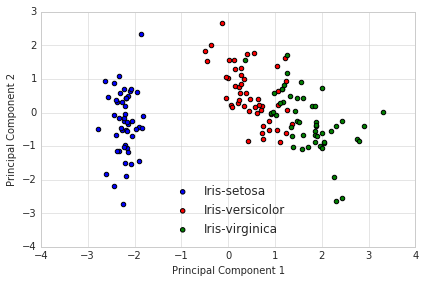
上图所示,我们通过PCA法得到新的更低纬度的子空间,样本在新的特征轴中“最分散”。
利用scikit-learn快速实现PCA
from sklearn.decomposition import PCA as sklearnPCA
sklearn_pca = sklearnPCA(n_components=2)
Y_sklearn = sklearn_pca.fit_transform(X_std)with plt.style.context('seaborn-whitegrid'):
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(Y_sklearn[y==lab, 0],
Y_sklearn[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()
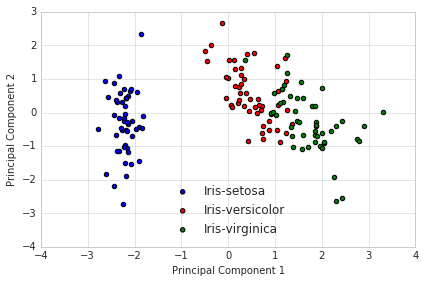
Covariance indicates the level to which two variables vary together. If we examine N-dimensional samples, X = [x_1, x_2, … x_N]^T, then the covariance matrix element C_{ij} is the covariance of x_i and x_j. The element C_{ii} is the variance of x_i.
参考:
http://www.csuldw.com/2016/02/28/2016-02-28-pca/
http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020209.html
