1.6.4 查找
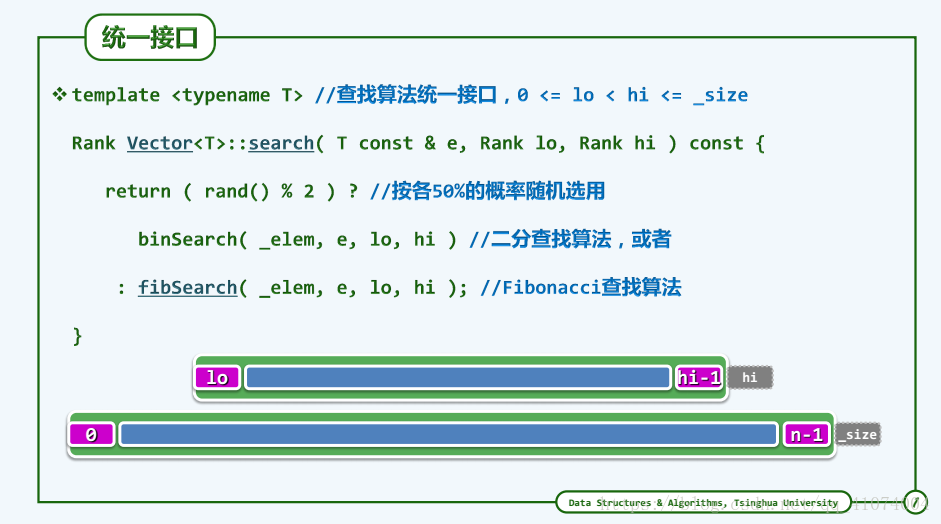
template <typename T> //在有序向量的区间[lo, hi)内,确定不大于e的最后一个节点的秩
Rank Vector<T>::search ( T const& e, Rank lo, Rank hi ) const { //assert: 0 <= lo < hi <= _size
return ( rand() % 2 ) ? //按各50%的概率随机使用二分查找或Fibonacci查找
binSearch ( _elem, e, lo, hi ) : fibSearch ( _elem, e, lo, hi );
}1.6.5 二分查找(版本A)
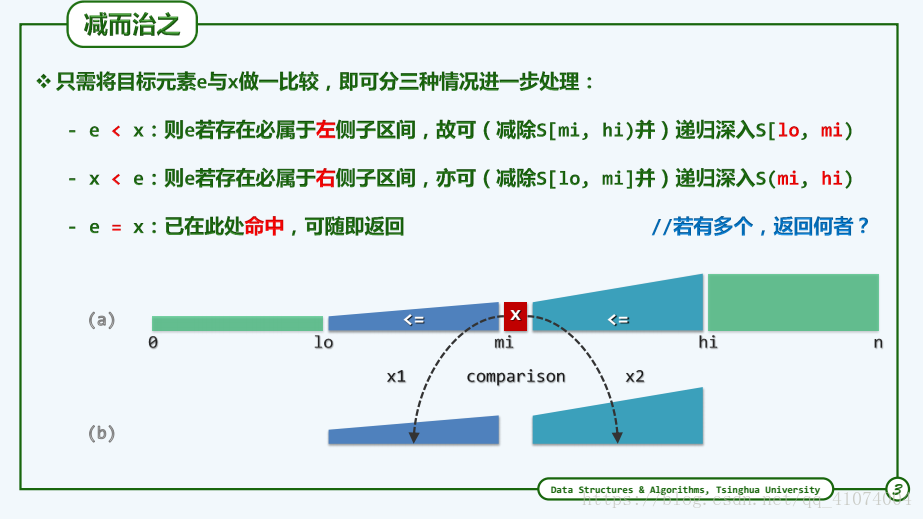
1.6.5.1 减而治之
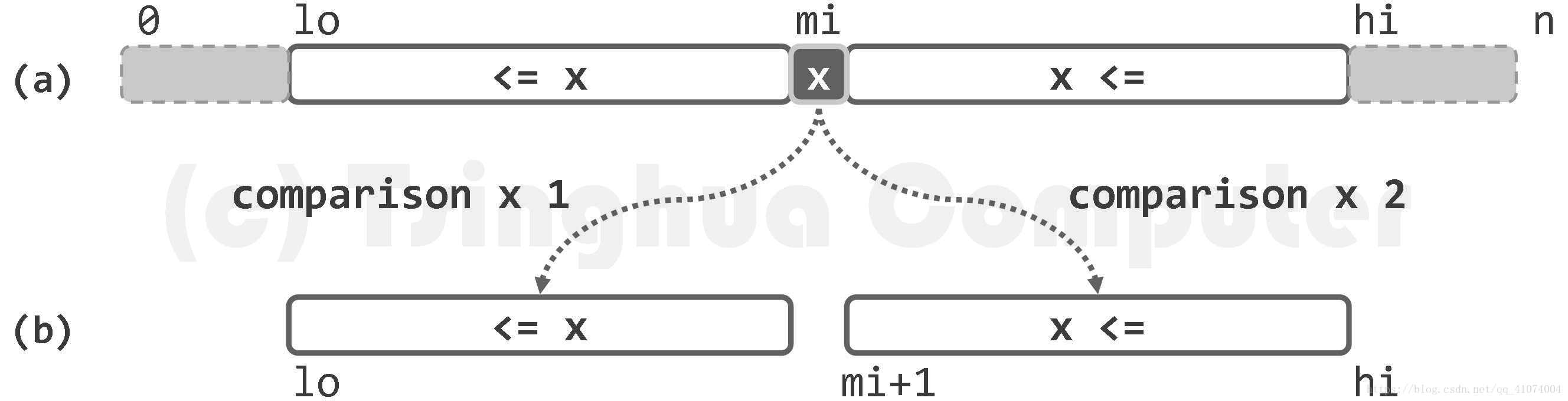
// 二分查找算法(版本A):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch ( T* A, T const& e, Rank lo, Rank hi ) {
/*DSA*/printf ( "BIN search (A)\n" );
while ( lo < hi ) { //每步迭代可能要做两次比较判断,有三个分支
/*DSA*/ for ( int i = 0; i < lo; i++ ) printf ( " " ); if ( lo >= 0 ) for ( int i = lo; i < hi; i++ ) printf ( "....^" ); printf ( "\n" );
Rank mi = ( lo + hi ) >> 1; //以中点为轴点
if ( e < A[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
else if ( A[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
else return mi; //在mi处命中
/*DSA*/ if ( lo >= hi ) { for ( int i = 0; i < mi; i++ ) printf ( " " ); if ( mi >= 0 ) printf ( "....|\n" ); else printf ( "<<<<|\n" ); }
} //成功查找可以提前终止
return -1; //查找失败
} //有多个命中元素时,不能保证返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
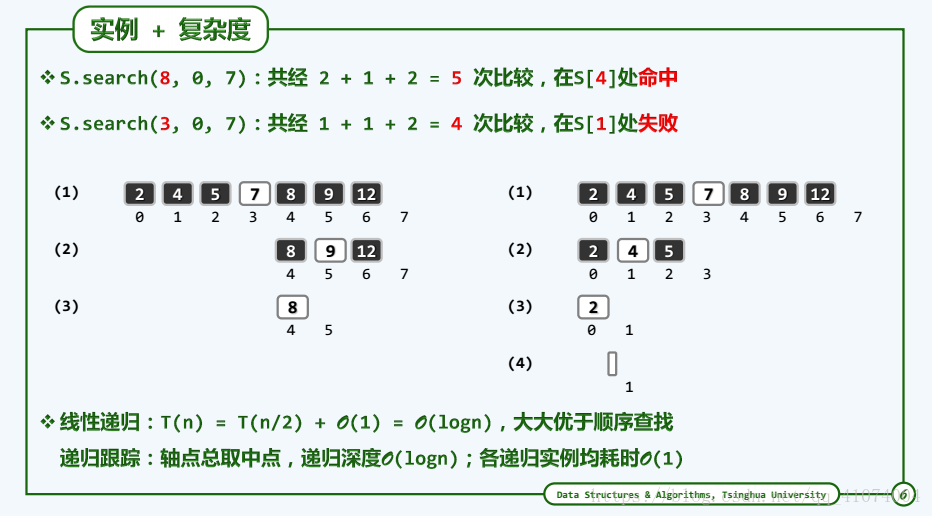
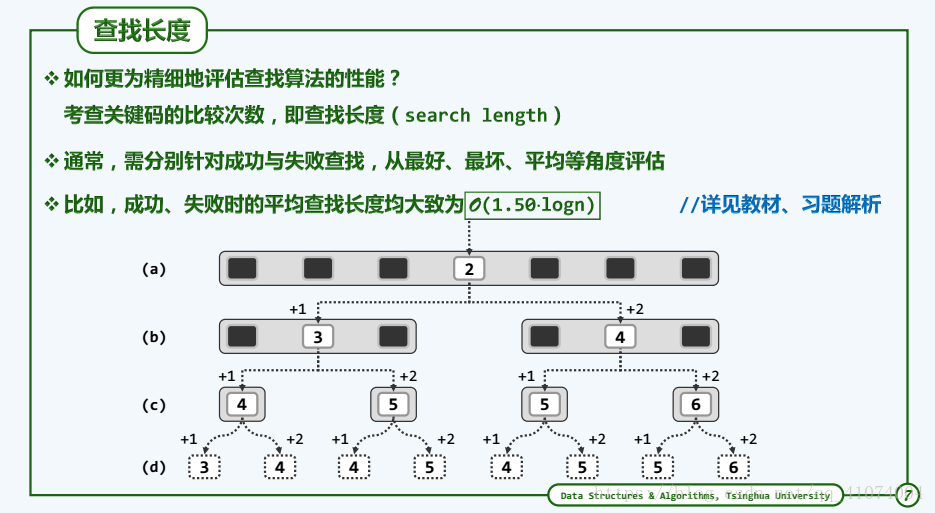
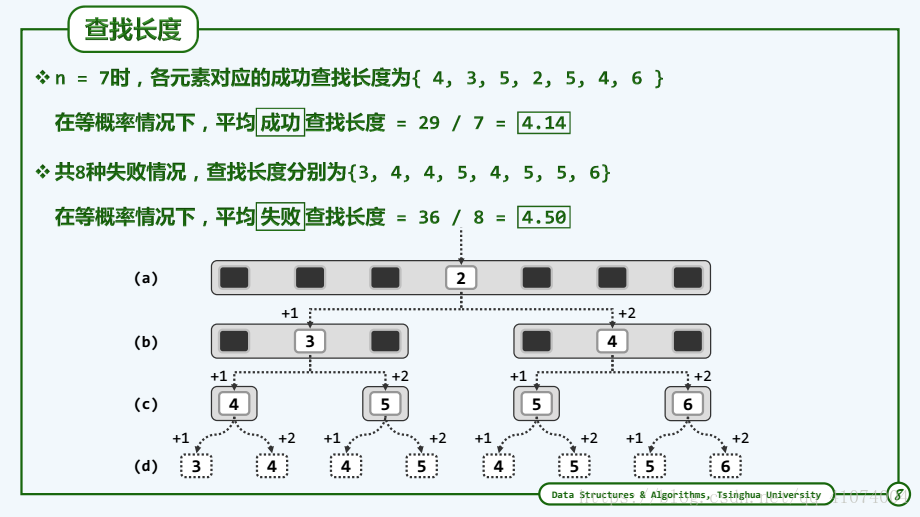
1.6.5.2 实例和复杂度
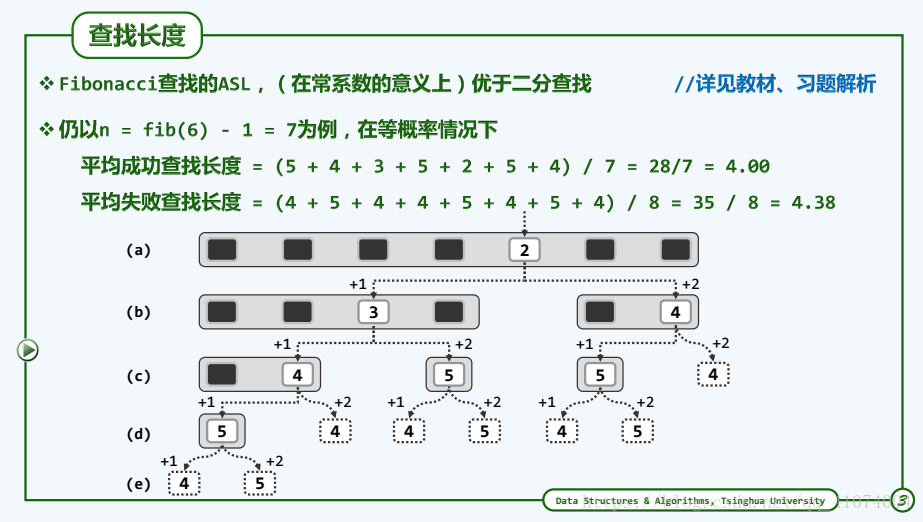
1.6.5.3 查找长度
成功查找长度以及失败查找长度(见课本P50 ===> P51)
1.6.6 Fibonacci查找
1.6.6.1 递推方程
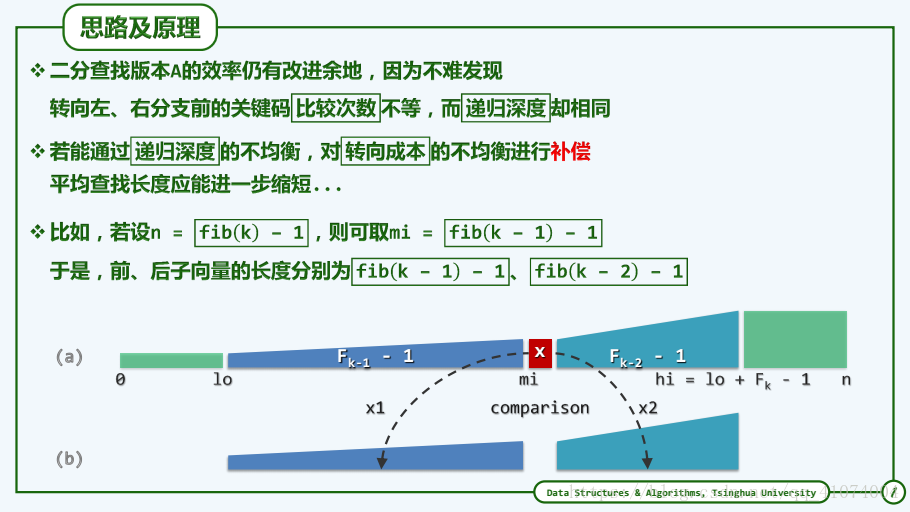
递推方程法既是复杂度分析的重要方法,也是我们优化算法时确定突破口的有力武器.
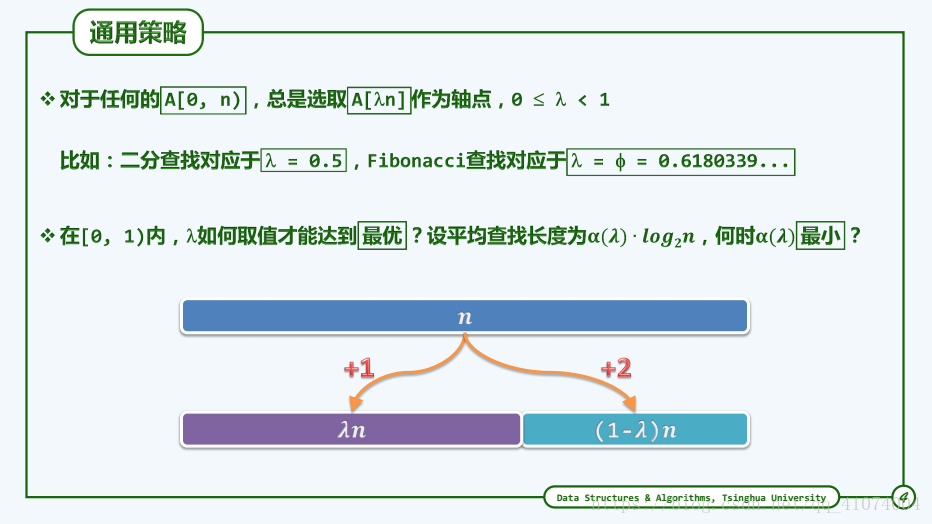
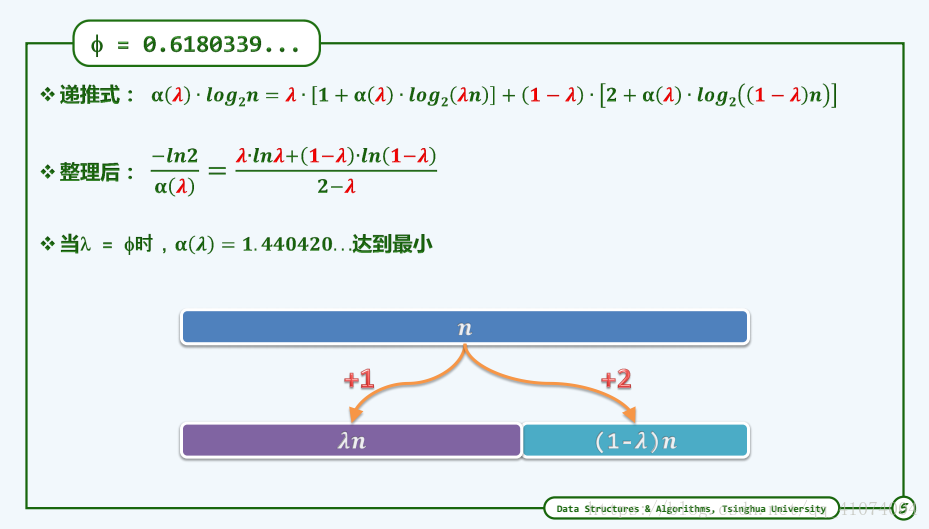
1.6.6.2 黄金分割
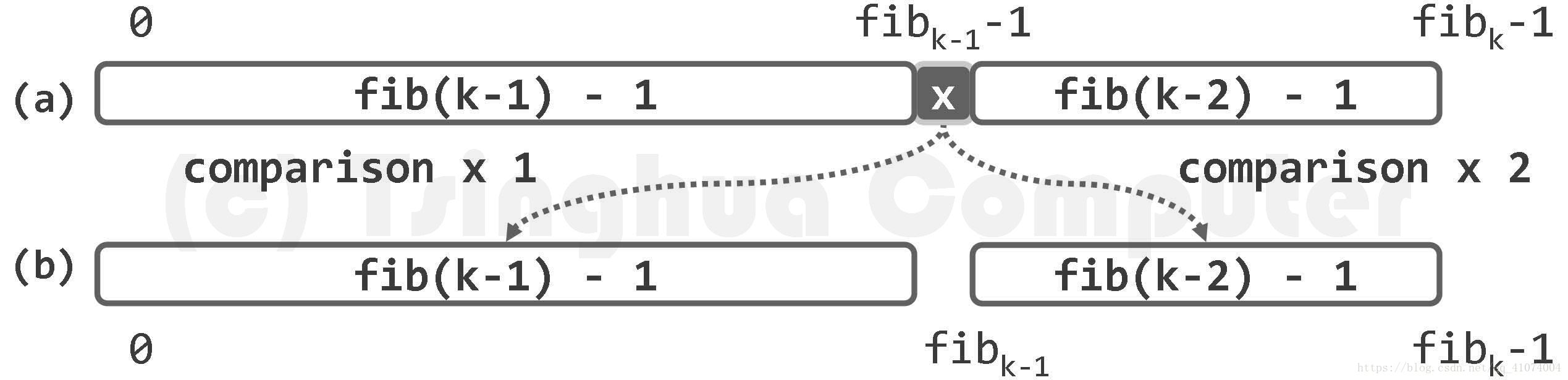
实际上,减治策略本身并不要求子向量切分点mi必须居中,故按上述改进思路,不妨按黄金分割比来确定mi。为了简化起见,不妨设向量长度 n = fib(k) - 1。
无论朝哪个方向深入,新向量的长度从形式上都依然是某个Fibonacci数减一,所以这种处理方法可以反复套用,直至因在S[mi]出命中或者向量长度收缩至0为止。
#include "..\fibonacci\Fib.h" //引入Fib数列类
// Fibonacci查找算法(版本A):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank fibSearch ( T* A, T const& e, Rank lo, Rank hi ) {
/*DSA*/printf ( "FIB search (A)\n" );
Fib fib ( hi - lo ); //用O(log_phi(n = hi - lo)时间创建Fib数列
while ( lo < hi ) { //每步迭代可能要做两次比较判断,有三个分支
/*DSA*/ for ( int i = 0; i < lo; i++ ) printf ( " " ); if ( lo >= 0 ) for ( int i = lo; i < hi; i++ ) printf ( "....^" ); else printf ( "<<<<|" ); printf ( "\n" );
while ( hi - lo < fib.get() ) fib.prev(); //通过向前顺序查找(分摊O(1))——至多迭代几次?
Rank mi = lo + fib.get() - 1; //确定形如Fib(k) - 1的轴点
if ( e < A[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
else if ( A[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
else return mi; //在mi处命中
/*DSA*/ if ( lo >= hi ) { for ( int i = 0; i < mi; i++ ) printf ( " " ); if ( mi >= 0 ) printf ( "....|\n" ); else printf ( "<<<<|\n" ); }
} //成功查找可以提前终止
return -1; //查找失败
} //有多个命中元素时,不能保证返回秩最大者;失败时,简单地返回-1,而不能指示失败的位置定性分析与定量分析( 见课本P53 ===> P 54)
关于黄金分割
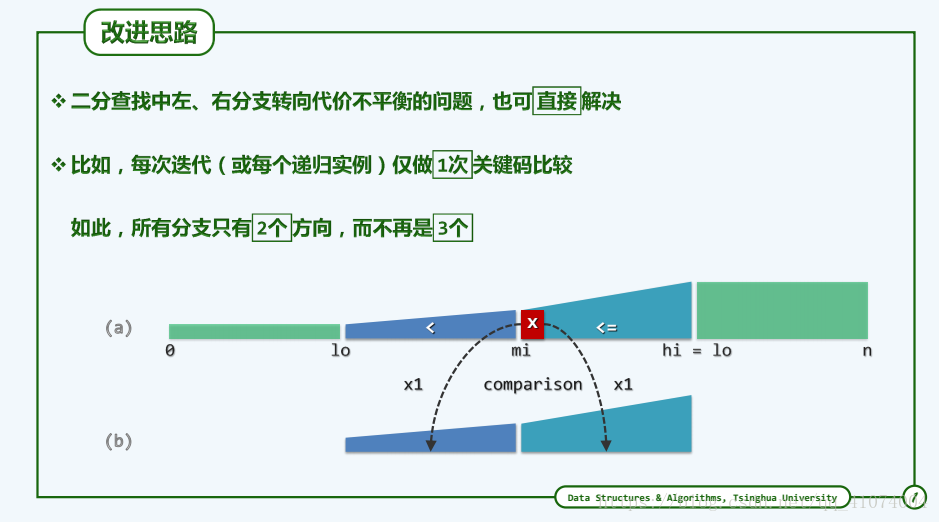
1.6.7 二分查找(版本B)
1.6.7.1 从三分支到两分支
// 二分查找算法(版本B):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch ( T* A, T const& e, Rank lo, Rank hi ) {
/*DSA*/printf ( "BIN search (B)\n" );
while ( 1 < hi - lo ) { //每步迭代仅需做一次比较判断,有两个分支;成功查找不能提前终止
/*DSA*/ for ( int i = 0; i < lo; i++ ) printf ( " " ); if ( lo >= 0 ) for ( int i = lo; i < hi; i++ ) printf ( "....^" ); printf ( "\n" );
Rank mi = ( lo + hi ) >> 1; //以中点为轴点
( e < A[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)
} //出口时hi = lo + 1,查找区间仅含一个元素A[lo]
/*DSA*/ for ( int i = 0; i < lo; i++ ) printf ( " " ); if ( lo >= 0 ) printf ( "....|\n" ); else printf ( "<<<<|\n" );
return ( e == A[lo] ) ? lo : -1 ; //查找成功时返回对应的秩;否则统一返回-1
} //有多个命中元素时,不能保证返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
2.6.8 二分查找(版本C)
// 二分查找算法(版本C):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch ( T* A, T const& e, Rank lo, Rank hi ) {
/*DSA*/printf ( "BIN search (C)\n" );
while ( lo < hi ) { //每步迭代仅需做一次比较判断,有两个分支
/*DSA*/ for ( int i = 0; i < lo; i++ ) printf ( " " ); if ( lo >= 0 ) for ( int i = lo; i < hi; i++ ) printf ( "....^" ); printf ( "\n" );
Rank mi = ( lo + hi ) >> 1; //以中点为轴点
( e < A[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)或(mi, hi)
} //成功查找不能提前终止
/*DSA*/ for ( int i = 0; i < lo - 1; i++ ) printf ( " " ); if ( lo > 0 ) printf ( "....|\n" ); else printf ( "<<<<|\n" );
return --lo; //循环结束时,lo为大于e的元素的最小秩,故lo - 1即不大于e的元素的最大秩
} //有多个命中元素时,总能保证返回秩最大者;查找失败时,能够返回失败的位置