DAG(Directed Acyclic Graph)图即无回路的有向图,在DAG上,一定有某些点不能由其他的点所到达,如果由多个这样的点,可以考虑加入一个新的点u,使得u到这些点有一条有向边,并且权值为0,即可转化成一个源点的DAG图。这种情况下,以DAG源点为源点的单源最短路径有特殊解法,使之拥有更高效率。
DAG上求单源最短路径算法,具体思想就是先得到DAG图的拓扑序列,然后按照拓扑排序的顺序处理每个点,必然是正确的,可以看下图了解,也可以了解差分约束系统中使用SPFA算法类似。
时间复杂度分析:对于DAG上的单源最短路径算法,在进行拓扑排序时,使用队列优化的寻找方法,可以使生成拓扑排序的时间效率为O(m)。虽然最后松弛操作有两层循环,但是两层循环的实质是遍历图中的每一条边仅仅一次,所以这一步的时间效率也是O(m),也就是说,这个算法的时间效率是O(m),可以说是非常高的算法。
题解:n和m的值都很大(1 ≤ n ≤ 100000, 0 ≤m ≤ 1000000),直接用无向图的求最短路算法肯定会超时,又注意到能构造的图其实是个有向无环图,所以就可以用求DAG图上的单源最短路径算法来解决了,其时间复杂度为O(m)。
这个算法只能求单源最短路啊,但是题目中明明说了可能有多个源点,并且告诉的不是边权而是点权。所以就得转换一下思路,重新构图。
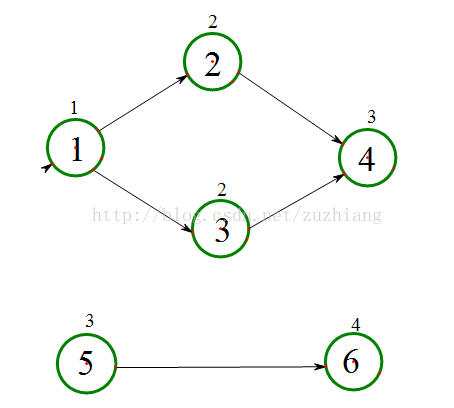
上图是根据题目给出的数据形成的图,可以很明显的得出结果为7。来重新构造一下图。
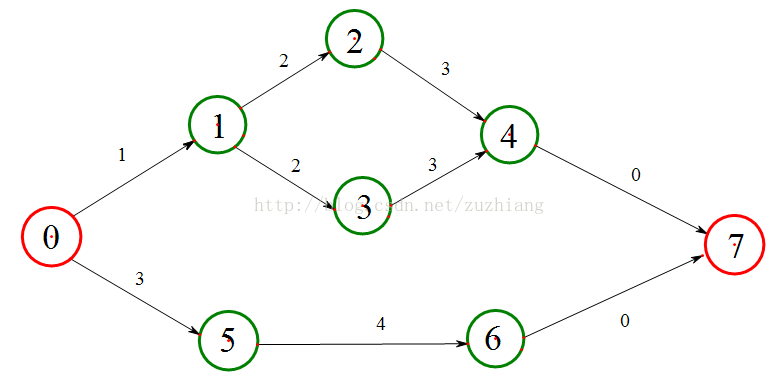
首先,加入一个超级源点(0点)和超级汇点(n+1点),让超级源点连接原来的所有源点,让原来的所有汇点连接超级汇点。然后还需要把点权转化为边权,具体做法是点 v 的点权转化为以 v 为入点的边上的边权,至于点到超级汇点之间的边权设为0。这样从某个源点走到某个汇点的最大距离就是从超级源点走到超级汇点的最大距离了。
具体实现:由于数据量很大,应该选用链式前向星的方式存储图结构,vector理论上也可以,但是肯定没有链式前向星好。首先根据给出的边和点权构图,将超级源点连接原来的所有源点,将原来的所有汇点连接超级汇点。接着跑一边拓扑排序,然后再根据拓扑序列求得最短路。
注意:
1.数据很大,结果应该用long long型存储。
2.求的是最大距离,所以要在最短路的基础上改一下。
3.传统的拓扑排序算法时间复杂度为O(n^2)会超时,我这里用了队列来优化,因为一个节点只有在删除与它相连的边的时候它的入度才可能变为0,只判断这些点并将入度为0的点入队会节省时间。
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
const int N=100010;
const int M=2000010;
struct edge{
int w,to,next;
};
edge edges[M];
int head[N];
int n,m,tol,cnt,w[N],chu[N],ru[N],que[N];
queue<int>q;
ll dis[N];
void read(int &x)
{
char ch=getchar();x=0;int f=1;
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
x*=f;
}
void init()
{
tol=0;
memset(head,-1,sizeof(head));
memset(chu,0,sizeof(chu));
memset(ru,0,sizeof(ru));
}
void add(int u,int v,int w)
{
edges[tol].w=w;
edges[tol].to=v;
edges[tol].next=head[u];
head[u]=tol++;
}
void toposort()
{
cnt=0;
q.push(0);
while(!q.empty()){
int top=q.front();
q.pop();
que[cnt++]=top;
ru[top]--;
for(int j=head[top];~j;j=edges[j].next){
ru[edges[j].to]--;
if(ru[edges[j].to]==0){
q.push(edges[j].to);
}
}
}
}
void solve()
{
dis[0]=0;
for(int i=1;i<=n+1;i++){
dis[i]=-inf;
}
for(int i=0;i<cnt;i++){
for(int j=head[que[i]];~j;j=edges[j].next){
int v=edges[j].to;
if(dis[v]<dis[que[i]]+edges[j].w){
dis[v]=dis[que[i]]+edges[j].w;
}
}
}
printf("%lld\n",dis[n+1]);
}
int main()
{
while(~scanf("%d%d",&n,&m)){
init();
int u,v;
for(int i=1;i<=n;i++){
read(w[i]);
}
for(int i=0;i<m;i++){
read(u);
read(v);
add(u,v,w[v]);
chu[u]++;
ru[v]++;
}
for(int i=1;i<=n;i++){
if(ru[i]==0){
add(0,i,w[i]);
ru[i]++;
}
if(chu[i]==0){
add(i,n+1,0);
ru[n+1]++;
}
}
toposort();
solve();
}
return 0;
}