PRML（一）如何根据贝叶斯理论推导多项式曲线拟合问题的cost function

马上要成为一个ML/DL方向的工程师，PRML作为经典教材，对于理解一些常用算法的intuition和motivation是非常有益的。虽然是2006年出版的一本书，但是有很多内容仍然值得学习和反思。加之本书有一些习题可以巩固思考，今天开始踏入PRML的学习。

① 理论基础

如何根据贝叶斯理论推导多项式曲线拟合问题的损失函数，这个需要的基本概率论基础如下

加法公式

$p (X) = \sum_{Y} p (X, Y)$ $p(X) = \sum_Y p(X,Y)$
乘法公式

$p (X, Y) = p (Y | X) p (X)$ $p(X,Y) = p(Y|X)p(X)$
贝叶斯公式

$p (Y | X) = \frac{p (X | Y) p (Y)}{p (X)}$ $p(Y|X) = \frac{p(X|Y)p(Y)}{p(X)}$
其中， $p (X, Y) = p (Y, X)$ $p(X,Y)=p(Y,X)$ , $p (X) = \sum_{Y} p (X | Y) p (Y)$ $p(X) = \sum_Y p(X|Y)p(Y)$
还有值得注意的是，在贝叶斯公式中，分母 $P(X)$ 被视为让条件概率之和为1（所有yi情况）的normalization constant——正则因子。
在后面叙述利用参数 $w$ 来作多项式拟合曲线中，我们假设先捕捉到关于 $w$ 的概率，用先验概率 $p(w)$ 表示。观测数据为 $D = \{ t_1, ... , t_N \}$ ，用条件概率 $p(D|w)$ 表示。 $p(D|w)$ 可以视为参数向量 $w$ 的函数，称为似然函数。因此，可以采用贝叶斯定理，形式如下：
$p (w | D) = \frac{p (D | w) p (w)}{p (D)}$ $p(w|D) = \frac{p(D|w)p(w)}{p(D)}$
PRML的作者Bishop不止一次强调： $p(D)$ 在贝叶斯公式中的作用就是让左边的 $p(w|D)$ 关于 $w$ 的积分为1，限制其规模，算是一个正则常数（normalization constatnt），即
$p (D) = \int p (D | w) p (w) d w$ $p(D) = \int p(D|w)p(w)dw$
在贝叶斯理论中，我们认为 $w$ 是不确定的，而 $D$ 是已知的——通过观测得到的唯一一组数据。贝叶斯理论的优点在于：先验知识的产生是自然的。比如对55开的投硬币问题，如果连续投3次，每次都是正面朝上，那么传统的最大似然估计估计就会错误的认为正面朝上的概率为1。而贝叶斯方法则会给出一个不会出现这种极端情况的先验概率。
当然，贝叶斯方法也有缺点，它的典型缺点是：先验分布是不提供信息的。贝叶斯方法的先验概率选择是基于数学上的方便而非其它先验信息的反映，所以，如果使用的贝叶斯方法先前的选择糟糕，那么会给糟糕的结果很高的置信度。

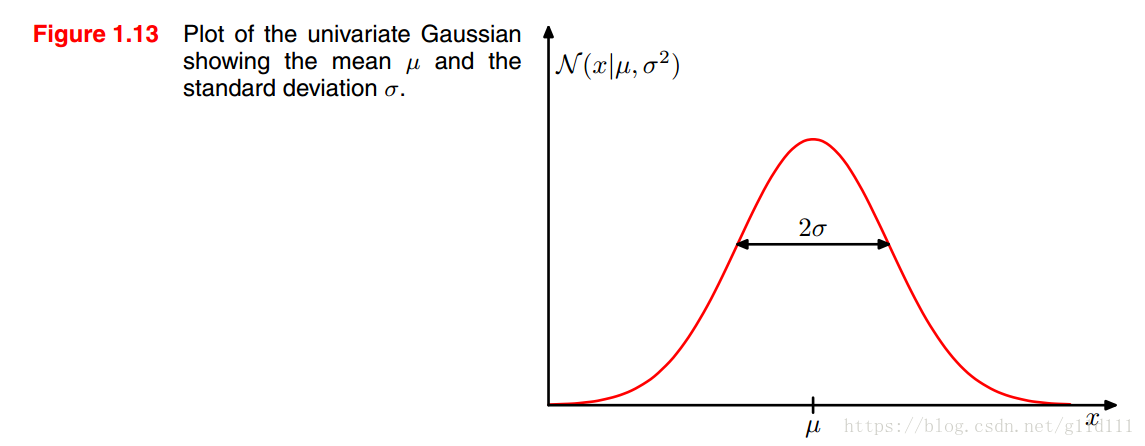
下面介绍一下高斯分布/正态分布，它是最为重要的一种分布，对于单个实值变量 $x$ ，其高斯分布为：

N (μ, σ^{2}) = \frac{1}{\sqrt{2 π σ^{2}}} e x p {- \frac{1}{2 σ^{2}} (x - μ)^{2}}

$N(\mu,\sigma^2) = \frac{1}{\sqrt {2\pi\sigma^2}} exp\{ -\frac{1}{2\sigma^2}(x-\mu)^2 \}$

其中， $\mu$ 为均值， $\sigma^2$ 为方差， $\sigma$ 为标准差。这里还定义了一个 $\beta = 1 / \sigma^2$ ，称为精度。
这里写图片描述

当 $x$ 为 $D$ 维向量组成的连续型变量时，其高斯分布的新形式为：
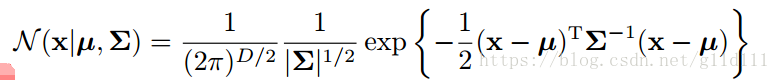
这里写图片描述
这里， $\sum = \sigma^T\sigma$ 为 $D$ x $D$ 的协方差矩阵。

现在，假设我们有一组观测值 $\mathbf x = \{ x_1, x_2, ..., x_N\}$ ， $N$ 表示样本个数。这里，我们认为这组观测值是独立服从高斯分布的，即independent and identically distributed——i.i.d（独立同分布）.由于数据集是独立同分布的，那么可以将数据集的概率写成如下形式：
这里写图片描述

根据概率理论，看起来应该对给定数据最大化参数的的概率比给定参数最大化数据更自然也一些。也就是 $xp(w|D)$ 比 $p(D|w)$ 更自然。但是贝叶斯方法正是通过求 $p(D|w)$ 进而得到 $p(w|D)$ 的，下面将正式开始推导过程的梳理。

② 根据贝叶斯理论推导多项式曲线拟合问题的cost function

2.1 曲线拟合问题再探

首先，让我们来看一下曲线拟合问题，这里，我们用概率论的视角重新解构多项式拟合问题。这对于我们了解损失函数中的主体和正则化项的形成会有更为清晰的认识。

曲线拟合的目标是根据新输入的变量 $x$ 来得到合理的预测 $t$ 。我们现在有一组( $N$ 个)输入数据 $\mathbf x = \{x_1, x_2, ..., x_N \}$ 和其对应值 $\mathbf t = \{ t_1, t_2, ..., t_N \}$ 。这里，可以通过概率分布来表达目标变量的不确定性——假设 $t$ 服从均值为 $y(x, \mathbf w)$ 高斯分布，表示如下：
这里写图片描述
这里的 $\beta^{-1}$ 就是前面提到的精度参数。

这里写图片描述

现在，通过最大似然估计，使用训练数据 $\{ \mathbf x ,\mathbf t \}$ 来找出未知参数 $\mathbf w$ 和 $\beta$ 的值。根据之前提到的，如果数据是独立同分布的，那么似然函数可以表示为：
这里写图片描述

显然，似然函数的对数形式更容易求解，其对数形式为：
这里写图片描述
这里，公式的后两项可以忽略，因为不包含 $w$ ；又log形式的最大似然函数系数不影响 $w$ 的取值。所以将 $\beta/2$ 用1/2替代；另外，最大化似然函数等价于最小化负log的似然函数。平方和误差函数看起来是从符合高斯分布的 $p(t|\mathbf w,\mathbf x,\beta)$ 导出的。通过这里，可以得到 $\mathbf w_{ML}$

同样地，可以通过最大似然估计求精度 $\beta$ ：
这里写图片描述

由于 $\mathbf w_{ML}$ 和 $\beta_{ML}$ 已经求出，我们可以据此得到 $p(w|D)$ ——之前一直求的是反直觉的 $p(D|w)$ 。

这里写图片描述

现在，引入多项式拟合问题的先验概率分布，为了简单，我们假定其服从高斯分布：
这里写图片描述
这里， $\alpha$ 表示分布的精度，也叫做超参数——hyperparameters； $M$ 为多项式的个数，也就是特征个数。

根据贝叶斯定理，关于 $\mathbf w$ 的后验分布与先验概率 X 似然函数成比例：
这里写图片描述

根据上面，我们的目标变为求后验概率的-log形式的最小值：
这里写图片描述
其中第一项取自

的第一项。第二项取自

的-log形式的 $exp\{-\frac{\alpha}{2} \mathbf w^T \mathbf w\}$

2.2 贝叶斯曲线拟合

尽管我们推出了先验概率 $p(\mathbf w| \alpha)$ 。到目前为止，我们还在对 $w$ 进行点估计，这还不完全等同于贝叶斯估计。在贝叶斯方法中，我们应该一贯的应用概率论的乘法和加法法则。

下面，我们假设上面推导过程中涉及到的 $\alpha$ ， $\beta$ 为固定值并提前知道其取值。贝叶斯方法将预测分布写成如下形式——忽略 $\alpha$ ， $\beta$ ：
这里写图片描述

注意，上式是服从高斯分布的，而且其可以进行解析分析。同样地，对上式进行积分，其高斯分布形式为：
这里写图片描述

公式（1.71）的第一项表示由于目标变量的噪声而导致的预测值 $t$ 的不确定性，第二项是由于参数 $\mathbf w$ 带来的不确定性，是贝叶斯处理过程中产生的。

其预测结果为合成正弦回归——synthetic sinusoidalregression 。
这里写图片描述