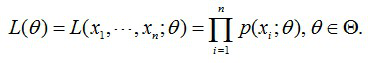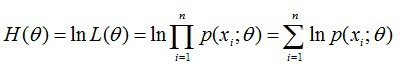EM(“Expectation Maximization”)期望最大化算法:它是一个基础算法,是很多机器学习领域算法的基础,比如聚类算法中的高斯混合模型(GMM),隐式马尔科夫算法(HMM), LDA主题模型的变分推断等等。
一、EM算法小栗子:
参考:https://www.jianshu.com/p/1121509ac1dc
•(1)假设有两枚硬币1和2,,随机抛掷后正面朝上概率分别为P1,P2。每次取一枚硬币,连掷5下,记录下结果,如下:
| 硬币 |
结果 |
统计 |
| 1 |
正正反正反 |
3正-2反 |
| 2 |
反反正正反
扫描二维码关注公众号,回复:
2678250 查看本文章

|
2正-3反 |
| 1 |
正反反反反 |
1正-4反 |
| 2 |
正反反正正 |
3正-2反 |
| 1 |
反正正反反 |
2正-3反 |
•得到P1和P2 的真实概率为:
P1 = (3+1+2)/ 15 = 0.4
P2= (2+3)/10 = 0.5
(2)以硬币的种类作为隐变量: Z
| 硬币 |
结果 |
统计 |
| Unknown |
正正反正反 |
3正-2反 |
| Unknown |
反反正正反 |
2正-3反 |
| Unknown |
正反反反反 |
1正-4反 |
| Unknown |
正反反正正 |
3正-2反 |
| Unknown |
反正正反反 |
2正-3反 |
把硬币的种类认为是一个5维的向量(z1,z2,z3,z4,z5),但是Z 是不知道的,就无法估计出P1和 P2,所以必须需要估计出Z, 再进一步地估计出P1 和P2.
(3)随便赋予P1和P2一个值,比如:
•P1 = 0.2, P2 = 0.7
•计算出每种情况下的的每个硬币的概率:
•如果是硬币1,得出3正2反的概率为 0.2*0.2*0.2*0.8*0.8 = 0.00512
如果是硬币2,得出3正2反的概率为0.7*0.7*0.7*0.3*0.3=0.03087
然后依次求出其他4轮中的相应概率。做成表格如下:
| 轮数 |
若是硬币1 |
若是硬币2 |
| 1 |
0.00512 |
0.03087 |
| 2 |
0.02048 |
0.01323 |
| 3 |
0.08192 |
0.00567 |
| 4 |
0.00512 |
0.03087 |
| 5 |
0.02048 |
0.01323 |
•按照最大似然法则:
第1轮中最有可能的是硬币2
第2轮中最有可能的是硬币1
第3轮中最有可能的是硬币1
第4轮中最有可能的是硬币2
第5轮中最有可能的是硬币1
•估计出的硬币的表格:
| 预测硬币(种类) |
真实硬币(种类) |
结果 |
统计 |
| 2 |
1 |
正正反正反 |
3正-2反 |
| 1 |
2 |
反反正正反 |
2正-3反 |
| 1 |
1 |
正反反反反 |
1正-4反 |
| 2 |
2 |
正反反正正 |
3正-2反 |
| 1 |
1 |
反正正反反 |
2正-3反 |
•根据Z 的估计值,按照最大似然函数来估计新的P1和P2,
•得到:
•P1 = (2+1+2)/15 = 0.33
P2=(3+3)/10 = 0.6
与真实概率值对比:
| 初始化的P1 |
估计出的P1 |
真实的P1 |
初始化的P2 |
估计出的P2 |
真实的P2 |
| 0.2 |
0.33 |
0.4 |
0.7 |
0.6 |
0.5 |
•使用估计出来新的P1和P2 值来估计Z ,反复迭代,最终得到实际的概率值
•这里有两个问题:
1、新估计出的P1和P2一定会更接近真实的P1和P2?
答案是:没错,一定会更接近真实的P1和P2,数学可以证明。
2、迭代一定会收敛到真实的P1和P2吗?
答案是:不一定,取决于P1和P2的初始化值,上面我们之所以能收敛到P1和P2,是因为我们幸运地找到了好的初始化值。
•改进版:
| 硬币 |
结果 |
统计 |
| Unknown |
正正反正反 |
3正-2反 |
| Unknown |
反反正正反 |
2正-3反 |
| Unknown |
正反反反反 |
1正-4反 |
| Unknown |
正反反正正 |
3正-2反 |
| Unknown |
反正正反反 |
2正-3反 |
•我们是用最大似然概率法则估计出的z值,然后再用z值按照最大似然概率法则估计新的P1和P2。也就是说,我们使用了一个最可能的z值,而不是所有可能的z值。
| 轮数 |
硬币1 |
硬币2 |
| 1 |
0.00512 |
0.03087 |
| 2 |
0.02048 |
0.01323 |
| 3 |
0.08192 |
0.00567 |
| 4 |
0.00512 |
0.03087 |
| 5 |
0.02048 |
0.01323 |
计算每轮使用硬币1和硬币2 的概率,使用硬币1的概率是:0.00512/(0.00512+0.03087)=0.14
使用硬币2的概率是1-0.14=0.86,依次算出5轮的概率:
| 轮数 |
硬币1 |
硬币2 |
| 1 |
0.14 |
0.86 |
| 2 |
0.61 |
0.39 |
| 3 |
0.94 |
0.06 |
| 4 |
0.14 |
0.86 |
| 5 |
0.61 |
0.39 |
我们就可以认为有0.14 的概率是硬币1,有0.86的概率是硬币2,而不是直接认为100%是硬币2.
•按照期望最大似然概率的法则来估计新的P1和P2:
•以P1估计为例,第1轮的3正2反相当于
0.14*3=0.42正
0.14*2=0.28反
依次算出其他四轮,列表如下:
| 轮数 |
正面 |
反面 |
| 1 |
0.42 |
0.28 |
| 2 |
1.22 |
1.83 |
| 3 |
0.94 |
3.76 |
| 4 |
0.42 |
0.28 |
| 5 |
1.22 |
1.83 |
| 总计 |
4.22 |
7.98 |
•P1=4.22/(4.22+7.98)=0.35
•可以看到,改变了z值的估计方法后,新估计出的P1要更加接近0.4。原因就是我们使用了所有抛掷的数据,而不是之前只使用了部分的数据。然后依次类推,继续迭代下去,直到算法收敛。
•估计求出 Z 的概率分布,称为E 步,依据最大似然估计求出P1和P2称为 M步。
二、极大似然函数:
•最大似然估计可以看作是一个反推。多数情况下我们是根据已知条件来推算结果,而最大似然估计是已经知道了结果,然后寻求使该结果出现的可能性最大的条件,以此作为估计值。极大似然值是最大化地逼近于真实参数值。

(1)样本集X={x1,x2,…,xN} N=100 (2)概率密度:p(xi|θ)抽到第i个样本的概率 , 100个样本之间独立同分布

表示在概率密度函数的参数是θ 时,得到X这组样本的概率, 需要找到一个参数θ,其对应的似然函数L(θ)最大这个叫做θ的最大似然估计量,记为
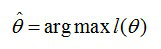
•求最大似然函数估计值的一般步骤:
•(1)写出似然函数;
•(2)对似然函数取对数,并整理;
•(3)求导数,令导数为0,得到似然方程;
•(4)解似然方程,得到的参数即为所求;
例子:给定一组样本 X1, X2, .....Xn, 已知它们是来自与高斯分布,估计参数, 结果算出估计值是与实际值是一样的。
三、Jensen不等式:
不同书籍对于凹函数,凸函数有不同的定义,我记得大学的高数知识中的定义是与本文相反的。
如果函数f(x), f(x)满足对定义域上任意两个数都有
,那么f(x)为凸函数
开口向下的是凸函数,开口向上的是凹函数。
•设f是定义域为实数的函数,如果对于所有的实数x。如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。当x是向量时,如果其hessian矩阵H是半正定的,那么f是凸函数。如果只大于0,不等于0,那么称f是严格凸函数。
•Jensen不等式表述如下:
•如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X])
•特别地,如果f是严格凸函数,当且仅当X是常量时,上式取等号。
f(x)=log x(高等数学写成 )为凹函数(其二次导数为-1/x2<0)
四、EM算法:
EM算法是迭代求解最大值的算法,同时算法在每一次迭代时分为两步,E步和M步。一轮轮迭代更新隐含数据和模型分布参数,直到收敛,即得到我们需要的模型参数。
1.算法推导
已知:样本集X={x(1),…,x(m))},包含m个独立的样本;
未知:每个样本i对应的类别z(i)是未知的(相当于聚类);
输出:我们需要估计概率模型p(x,z)的参数θ;
目标:找到适合的θ和z让L(θ)最大。
对于每一个样例i,让



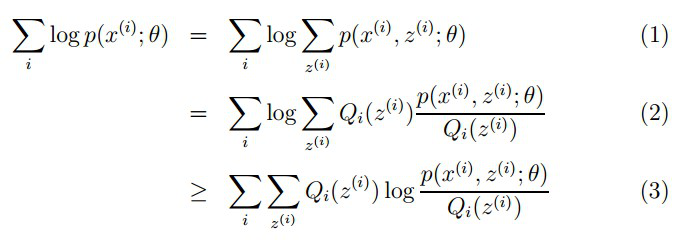
(2)(3)式是利用Jensen不等式,且 函数式凹函数,所以有:
由Lazy Statistician规则可得:
(1) X是离散型随机变量,它的分布律为
,k=1,2,…。若
绝对收敛,则有
有:

对应于上述问题,Y是





要使L(θ)最大,我们可以不断最大化下界J,来使得L(θ)不断提高,达到最大值。
什么时候下界J(z,Q)与L(θ)在此点θ处相等?
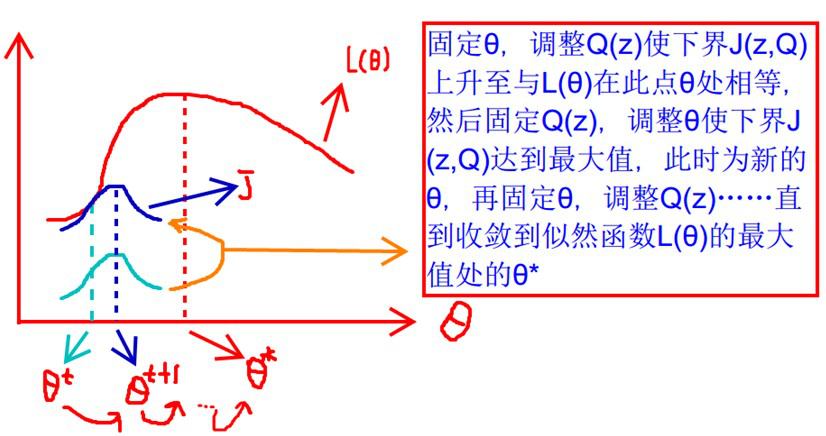
可以通过调整这两个概率使下界不断上升,以逼近

根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到:
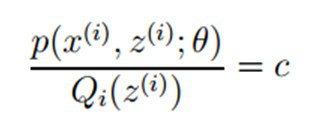
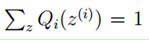
对此式子做进一步推导,我们知道

放到右边, 同时对等式两边式子进行累计求和,所以可以得到

所以有:
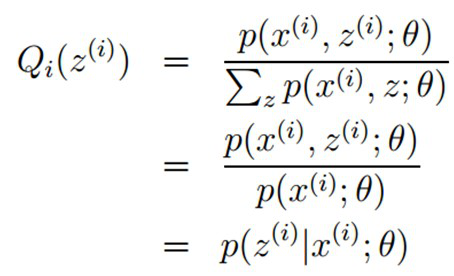
至此,我们推出了在固定其他参数







2、算法流程
1)初始化分布参数θ; 重复以下步骤直到收敛:
E步骤:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。作为隐藏变量的现估计值:

M步骤:将似然函数最大化以获得新的参数值:
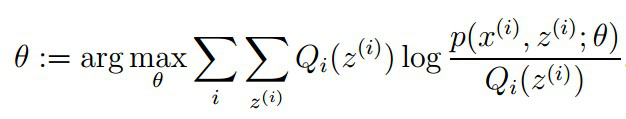
EM算法缺陷之一:传统的EM算法对初始值敏感,聚类结果随不同的初始值而波动较大。总的来说,EM算法收敛的优劣很大程度上取决于其初始参数。
参考:徐亦达老师的讲解
https://www.jianshu.com/p/1121509ac1dc
https://www.cnblogs.com/pinard/p/6912636.html