近期流行的生成模型
本次介绍近期大火的三大类生成模型,这三大类模型从三个不同角度切入,居然都能有惊人的效果。而且深入挖掘发现它们有很多相似的地方。
1. Generative Adversarial Nets
生成对抗网络(GANs)是当今最火的生成模型,从2014年 Goodfellow 论文发表开始,其引用量已是4000+了。而且GANs家族人丁兴旺,从最原始的GANs开始,家族明星是一个接一个,如cGAN, DCGAN, WGAN,WGAN-GP,LSGAN,BEGAN,infoGAN,seqGAN,cycle-GAN,star-GAN等等,每一个出来都是一个新闻。
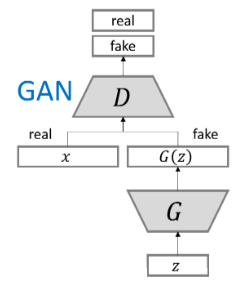
GANs的火热最直接的原因,其原理直观,可解释。生成模型的目的常常是为得到数据X的分布p(X)。而常常我们对数据的分布一无所知,甚至很多数据分布是没有解析式的。GANs来求解p(X)时,走了一条不同寻常的路。GANs采用对抗的方式来学习,或者说是模仿(mimic)的方式来学习。GANs有个生成器(G),它的目的是生成可以以假乱真的数据,为了更好的训练G,GANs引入一个判别器(D),它的工作是当一个样本经过它之后,它能判别出样本是真实的数据样本还是生成器生成的样本,即它输入一个值来代表样本为真的程度。正如原文的例子一样,G相当于一个假币制造者,而D 是警察。就在这个互相对抗中,G生成的样本越来越像直实数据,而D的判别能力也越来越高。用公式表示即是:
\[\min_{G}\max_{D} E_{x\sim p(x)} D(x) + E_{z\sim p(z)}[1 - D(G(z))]\]
GANs家族欣欣向荣,如上面提到的都是明星GANs,那么问题来了,谁会更好,有没有在各个方面全面超越其它GANs的?Google给出答案8,在2017年它们把当时主要的GANs变种放在一起研究,竟发现它们都差不多~。
2. Variational Autoencoders
变分自编码器(VAE)是另一种非常著名的生成模型,常常将其与GANs相提并论。VAE虽然在学术界很有名,但很多人对它并不是很了解,一部分原因是VAE的名字很高大上,会有人觉得比较难从而望而却步;还有一些原因是没有太多讲解的比较好的, 通俗但又不失逻辑的博文。其实最主要的原因是VAE真的涉及比较多的知识,从而仅有的几篇好资料还是从不同角度切入,这为初学者带来不小的障碍。VAE的第一手资料当然是原始论文,但因为是大师手笔,其把他们认为‘显而易见’而对我们至关重要的过程给省略了,所以也比较难读。
从字面可知VAE至少包含两块内容,变分推断(Variational Inference)与自编码器(Auto encoders)。
首先,变分推断在VAE当中,可以简单的理解为KL散度的应用即可。其次,自编码器是因为VAE的结构与自编码器很像,都有解码与编码过程。
首先来看auto encoder的结构:
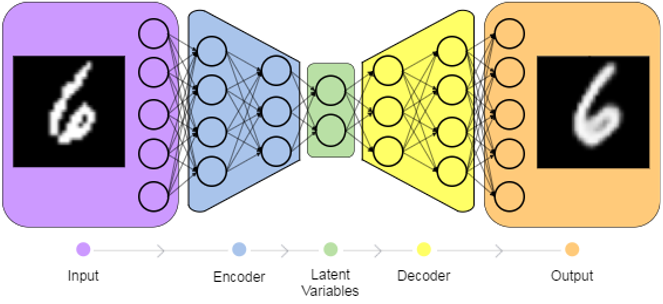
Input: X 经过auto encoder生成\hat X,如果二者相似,说明auto encoder的是一个可用的模型。
auto encoder模型涉及两过程:编码(encoding)与解码(decoding)。通常认为X的生成是由某些隐变量(latent variables,记为Z)决定的。所以变程可分解为:
\[ X \xrightarrow{ P(Z|X) \quad (encoder)} Z\xrightarrow{P(\hat X|Z)\quad (decoder)} \hat X \]
生成模型首先想到最大似然:
\[ P(X) = \int P(X|Z)P(Z) dZ \]
但有隐变量的存在,简单的MLE是不行了的,那么可否用EM算法呢,因为EM算法会涉及到模型:P(Z|X)
\[ P(Z|X) = \frac{P(X|Z)P(Z)}{P(X)} \]
因为P(X)中有积分的存在,且分布未知,是不可处理的(Intractable),所以EM算法也无能为力。
那么,还有的方法就是Gibbs釆样法与变分推断了。Gibbs采样法与即将采用的神经网络,梯度下降法是不合拍的。
P(Z|X)不可处理,那么我们可以用一个可用处理的分布(设为Q(Z))来近似P(X|Z)。根据变分推断,Q(Z)与P(Z|X)的近似程度(更确切地说是距离)可用KL散度来刻画:
\[Q^*(Z) = \arg \min_{Q(Z)\in \mathscr{Z}} KL(Q(Z)||P(Z|X))\]
其中\(KL(Q|P) = E_{z\sim Q}\left[\log Q(Z) -\log P(Z|X)\right] = \int Q(Z)\log\frac{Q(Z)}{P(Z|X)} dZ\). 做下简要推导(把3式即贝叶斯法则代入):
\[ \begin{array}\\ KL(Q(Z)||P(Z|X)) &= E_{z\sim Q}\left[\log Q(Z) -\log P(Z|X)\right] \\ &= E_{z\sim Q}\left[\log Q(Z) -\log \frac{P(X|Z)P(Z)}{P(X)}\right]\\ & = E_{z\sim Q}\left[\log Q(Z) -\log P(X|Z)- \log P(Z) + \log P(X)\right] \\ &= E_{z\sim Q}\left[\log Q(Z) -\log P(X|Z)- \log P(Z)\right] + \log P(X) \quad(\text{因为}P(X)\text{不依赖于}Z)\\ \end{array} \]
经变换可得:
\[ \begin{array}\\ \log P(X)& =& -E_{z\sim Q}\left[\log Q(Z) -\log P(X|Z)- \log P(Z)\right] + KL(Q(Z)||P(Z|X))\\ &=& -E_{z\sim Q}[\log Q(Z) - \log P(Z)] + E_{z\sim Q} \log P(X|Z) + KL(Q(Z)||P(Z|X))\\ &=& -( - E_{z\sim Q} \log P(X|Z) + KL [ Q(Z) || P(Z)] ) + KL(Q(Z)||P(Z|X))\\ && 其中Q(Z)可以是任意函数,但我们更关心的是依赖于X的那部分,\\ &&所以可以将上式中的Q(Z)替换成Q(Z|X):\\ &=& -( - E_{z\sim Q} \log P(X|Z) + KL [ Q(Z|X) || P(Z)] ) + KL(Q(Z|X)||P(Z|X))\\ & = & ELBO + KL(Q(Z|X)||P(Z|X)) \end{array} \]
其中\(ELBO (evidence lower bound) = -( - E_{z\sim Q} \log P(X|Z) + KL [ Q(Z|X) || P(Z)] )\).
从MLE的角度,最大化\(\log P(X)\)可转化成最大化ELBO(因为KL非负),这也是ELBO名字的由来。从变分的角度,最小化KL可转化成最大化ELBO,因为在这个背景下,可认为\(\log P(X)\)是固定的(evidence)。ELBO是可处理的。
我们知道对任一x,它都可以转化成y,无论二者间的转化函数多么复杂。那么我们可以假设Q(Z|X)与P(Z)(后验与先验)为正态分布,事情就容易了,而且更近一步,尽管变得可处理了,但因为参数过多,用神经网络来近似再好不过了:
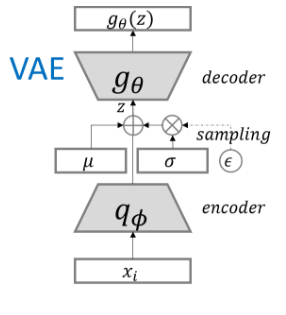
从上图可知,encoder在X给定的前提下,会产生两个参数向量,\(\mu(X)\)和 \(\sum (X)\)。但这会产生两个问题,一个是在此分布上做抽样方差会很大,另一个是抽样这个方式本身是不可导的。
The Reparameterization Trick
为解决上述问题,这里用到了一个trick,即为得到隐变量z,我们不是从N(\mu(X),\sum(X))中抽样,而是从标准正态分布中抽取,变经变换:\(z = \mu(X) + \sum^{\frac{1}{2}}(X)\cdot\epsilon\),其中\(\epsilon \sim N(0,1)\)。
3. Flow-based Model
Flow-based的模型就没有以上两种那么的有名了,而且可以说是郁郁不得志,在2014年NICE(最初版flow-based模型)提出时,关注者寥寥。在2016年改进版问世时,也没啥动静,直到2018年OpenAI的glow横空出世,终于划过夜空,让大家见到了这个一时竟盖过GANs和VAEs,风头正劲的生成模型。
flow-based模型的思想也很直观: 寻找一种变换h = f(x)(f 可逆,且h与x的维度相同)将数据空间映射到另一个空间,新空间各个维度相互独立:
\[ p_H(h) = \Pi_d p_{H_d}(h_d) \]
新的空间数据的组织结构相对简单。换种说法即是,我们要学习的是样本的分布,通过一种可逆变换将这个分布转化成一种相简单易得的分布,比如指数族分布。
将变量转换可得到:
\[ p_X(x) = p_H (f(x))| \det \frac{\partial f(x)}{\partial x}| \]
这个推导是由概率中的变量转换定理给出的:
\[ \begin{array}\\ F_X(x) = P(X\le x) = P(g(h)\le x) = P(h \le f(x)) = F_H(f(x)) \end{array} \]
其中 \(g(\cdot)\)为 \(f(\cdot)\) 的反函数,两边同时对x求导即可。
变换\(f(\cdot)\)需是其雅克比矩阵(\(\frac{\partial f(x)}{\partial x}\))比较容易得到,且其反函数\((g(\cdot))\)也容易得到。
通过最大似然法优化:
\[ \log (p_X(x)) = \log(p_H(f(x))) + \log(|\det \frac{\partial f(x)}{\partial x}|) \]
其中\(p_H(h)\)为先验,是预先给定的,比如标准正态分布。如果这个先验可因式分解(即各维度相互独立),那么我们可称为非线性独立成分估计(Non-Linear Independent components estimation(NICE)).
如果是NICE,上面的形式即可转化为:
\[ \log (P_X(x)) = \sum_{d =1}^D\log (p_{H_d}(f_d(x))) + \log(|\det(\frac{\partial f(x)}{\partial x})|) \]
其中\(f(x) = (f_d(x))_{d\le D}\), 另外 f(\cdot)可以是由一系列的变换组成的总变换\(f =f_1\circ f_2\circ...\circ f_K\)(就像深度神经网络一样,只不过要求每变换f_k都必须是可逆的):
\[ x \overset{f_1}{\underset{f_1^{-1}} \Longleftrightarrow}h_1 \overset{f_2}{\underset{f_2^{-1}} \Longleftrightarrow} h_2\overset{f_3}{\underset{f_3^{-1}} \Longleftrightarrow}... \overset{f_K}{\underset{f_K^{-1}} \Longleftrightarrow}h_K \]
\[ \log p_X(x) = \sum_{d = 1}^D \log(p_{H_d}(f_d(x))) + \sum_{i=1}^K \log|\det(\frac{\partial h_i}{\partial h_{i-1}})| \]
Coupling Layer
上面提到\(f(\cdot)\)应该满足:可逆且反函数易得,雅克比矩阵也要易得。作者提出了一种双射变换。
设 \(x \in \mathscr{X}, I_1,I_2\)是 [1,D]的两个分量,令 \(d = |I_1|\) 并且 m 是定义在 \(R^d\)上的函数,且令 $y = (y_{I_1},y_{I_2}), y_{I_1},y_{I_2} $满足:
\[ \begin{array}\\ y_{I_1} = x_{I_1}\\ y_{I_2} = g(x_{I_2},m(x_{I_1})) \end{array} \]
可以看出这是一种可逆变换:
\[ \begin{array}\\ x_{I_1} = y_{I_1}\\ x_{I_2} = g^{-1}(y_{I_2}; m(y_{I_1})) \end{array} \]
从上式可知,\(m(\cdot)\)在可逆变换中并不没有变换,也不影可逆变换,那么\(m(\cdot)\)可以是任意复杂的,比如各种神经网络。
而且此变换的雅克比矩 以阵也容易得到:
\[ \frac{\partial y}{\partial x} = \left[ \begin{array}\\ I_d \quad\quad 0\\ \frac{\partial y_{I_2}}{\partial x_{I_1}} \quad\frac{\partial y_{I_2}}{\partial x_{I_2}} \end{array} \right] \]
其中 I_d是单位阵,这也意味着:
\[ \frac{\partial y}{\partial x} = \det \frac{\partial y_{I_2}}{\partial x_{I_2}} \]
Glow
glow 是OpenAI 在NICE,与Real NVP的基础上的做的工作,理论没有变化只是在原基础上做了一个优化,即在此篇论文中提出一个叫做 step of flow 模块(左下).
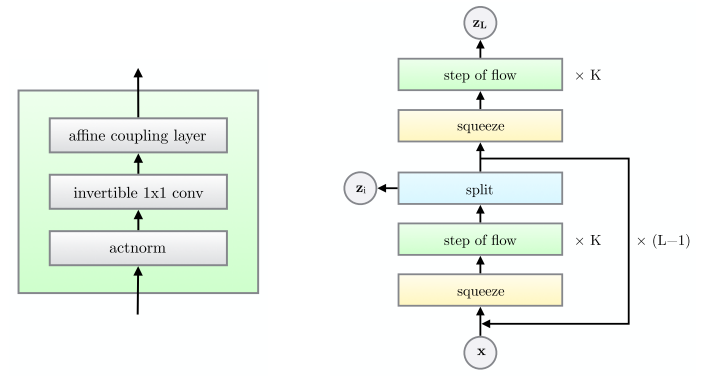

Tricks
Rescaling
如果采用加法式coupling layer(也即 g = a +b), 那么雅克比矩阵就退化成为单位阵,这样显然对学习不利,因此添加额外一层,此层为一个对角矩阵 S 去将coupling layer 的能量释放出来,这样,优化函数也变为:
\[\log(p_X(x)) = \sum_{i = 1}^D [\log(p_{H_i}(f_i(x))) + \log(|S_{ii}|)]\]
Masked convolution
coupling layer的变换 f 可以写成:
\[ y = b\odot x + (1-b)\odot\Big (g \big((1-b)\odot x; m(b\odot x)\big)\Big) \]
其中b是一个二元的 mask. b的形式有很多,如(0,0,...,1,1), (1,0,1,0,1,...),甚至可以是随机的。
Combining coupling layers
多个coupling layers 叠在一起的能力会更强大。但要注意,因为每一层的coupling layer都有一部分的雅克比行列式是单位阵,这样在优化的时候如果在每一层都同一部分的雅克比矩阵是不变的单位阵,不利于学习,因此最好两部分(如上面的I_1,I_2)可以交换的变换角色。
Multi-scale architecture
为节省计算量与存储消耗,都只将上一层的一部分经过新的layer:
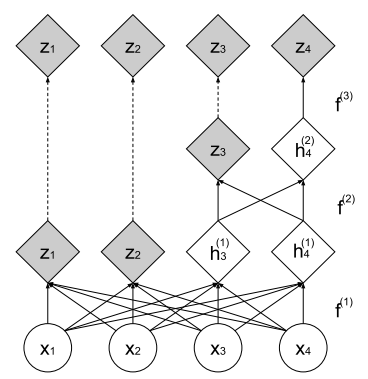
用公式可表示为:
\[ \begin{array}\\ h^{(0)} = x\\ (z^{(i+1)},h^{(i+1)})) = f^{(i+1)}(h^{(i)})\\ z^{(L)} = f^{(L)}(h^{(L-1)})\\ then\\ z = (z^{(1)},...,z^{(L))}) \end{array} \]
Batch normalization and residual networks
pass
三者在结构上可能有些差别,理论出发点也各不相同,但你会发现三者竟是共通的,他们其实都是将数据映射到新的空间,这个空间的数据分布相对易得。
主要参考文献
[1]: Kingma, D. P., Dhariwal, P., & Francisco, S. (n.d.). Glow: Generative Flow with Invertible 1×1 Convolutions, 1–15. Retrieved from https://github.com/openai/glow.
[2]: Dinh, L., Sohl-Dickstein, J., & Bengio, S. (2016). Density estimation using Real NVP. https://doi.org/1605.08803
[3]: Dinh, L., Krueger, D., & Bengio, Y. (2014). NICE: Non-linear Independent Components Estimation, 1(2), 1–13. https://doi.org/1410.8516
[4]: Kingma, D. P., & Welling, M. (2013). Auto-Encoding Variational Bayes, (Ml), 1–14. https://doi.org/10.1051/0004-6361/201527329
[5]: Doersch, C. (2016). Tutorial on Variational Autoencoders, 1–23. https://doi.org/10.3389/fphys.2016.00108
[6]: Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., … Bengio, Y. (2014). Generative Adversarial Networks, 1–9. https://doi.org/10.1001/jamainternmed.2016.8245
[7]: Mirza, M., & Osindero, S. (2014). Conditional Generative Adversarial Nets, 1–7. Retrieved from http://arxiv.org/abs/1411.1784
[8]: Lucic, M., Kurach, K., Michalski, M., Gelly, S., & Bousquet, O. (2017). Are GANs Created Equal? A Large-Scale Study. Retrieved from http://arxiv.org/abs/1711.10337