本文转载自多个地方,仅用作个人学习,如需删除请见谅并联系本人。
1 梯度下降法
2 坐标下降法
1.首先给定一个初始点,如 X_0=(x1,x2,…,xn);
2.for x_i=1:n
固定除x_i以外的其他维度
以x_i为自变量,求取使得f取得最小值的x_i;
end
3. 循环执行步骤2,直到f的值不再变化或变化很小.
3 牛顿迭代法
牛顿迭代法(Newton’s method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
把f(x)在x0点附近展开成泰勒级数 f(x) = f(x0)+(x-x0)f’(x0)+(x-x0)^2*f”(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f’(x0)(x-x0)=0 设f’(x0)≠0则其解为x1=x0-f(x0)/f’(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f’(x(n))。
4 最小二乘法与梯度下降法区别
最小二乘是构建目标函数中的一种方法;
梯度下降是求解最优目标函数中的一种方法。
对于变量个数为2-3个的目标函数,可以直接用方程组的方式求解出来,这也就是我们常见的狭义上的最小二乘法。
对于变量个数多个的目标函数,这时,狭义的最小二乘法就难以胜任,而用梯度下降法求解就容易多了。
http://www.cnblogs.com/wacc/p/4870043.html
1.1 什么是凸集?
简单来说, 凸集是一个点集, 这个点集有一个性质, 就是在这个集合中任取不同的两个点x和y, 他们之间的线段(包括端点)上的点都属于这个点集,那么就说这个点集是一个凸集。

比如下图中左边的图形是凸集,而右边不是,因为我们可以找到两个点,使它们之间的线段上的点不在集合中
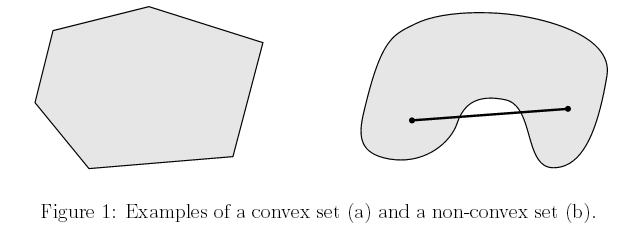
数学上,凸集的定义如下:
给定集合,,,如果有
我们就称集合C是凸集,我们把点称为x和y的凸组合。
1.2 什么是凸函数?
假设有一个函数,记其定义域为,如果是凸集,且在其中任取两个点,满足以下性质:
那么就称为凸函数。
注意:定义域是凸集这个要求不是必须的,其出发点只是为了使x,y的凸组合有定义
关于凸函数,直观上可以用下图来加深理解:
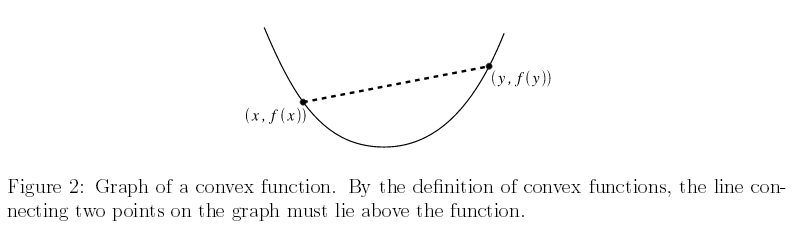
简单来说,我们在定义域任取两个点x,y, 连接他们得到一条线段,如果这个线段上的点都位于对应函数值上方,我们就说该函数是一个凸函数。
更进一步,如果且我们称是严格凸的。如果是凸函数,那么就是凹函数。如果是严格凸函数,那么就是严格凹函数。
1.3 凸函数的等价判别方法
上面我们讲了什么是凸函数,然而这个定义在现实中很难用于判断一个函数是不是凸的,因此介绍几个等价的定义。
1.3.1 一阶近似
假设函数是可导函数(也就是说的梯度在整个定义域上都存在),则是凸函数当且仅当 其定义域是凸集,且对于所有的有下式成立:
我们将叫做对f的一阶近似,其物理意义实际上是经过点x的切平面,我们用这个切平面上的点来近似。这个公式的含义是:如果f是凸函数,那么它的一阶近似值始终位于函数值的下方。
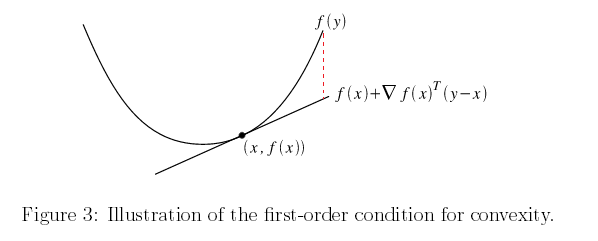
1.3.2 二阶近似
假设函数二阶可导(即海塞矩阵在定义域上都有定义),则f是凸函数当且仅当 其定义域是凸集且其海塞矩阵半正定,即:
可能有些同学忘了海塞矩阵长什么样了,这里提一下。假设我们的变量来自n维空间,即,我们记,即由n个变量组成的向量。那么海塞矩阵(记为H吧)是一个的方块矩阵,且
也就是说,是f(x)分别对和进行求导两次得到的。
1.4 凸优化问题
上面已经介绍了凸集和凸函数,是时候到凸优化了吧? 别急,在介绍凸优化概念之前再啰嗦两句。
1.4.1 水平子集(sublevel sets)
由凸函数的概念出发,我们可以引出水平子集(sublevel set)的概念。假定f(x)是一个凸函数, 给定一个实数,我们把集合
叫做水平子集。 也就是说水平子集是所有满足的点构成的集合。利用凸函数性质,我们可以证明水平子集也是凸集:
水平子集告诉我们,给凸函数添加一个上限,定义域内剩下的点构成的点集还是一个凸集。
1.4.2 仿射函数(affine functions)
数学上,我们把形如
的函数叫做仿射函数。其中,,一个向量。直观上理解,仿射函数将一个n维空间的向量通过线性变换A映射到m维空间,并在其基础上加上向量b,进行了平移。
同理,我们可以证明,点集
是一个凸集,证明略。
1.4.3 凸优化(convex optimization)
那么回到凸优化问题上来, 什么是一个凸优化问题?
一个凸优化问题可以定义为:
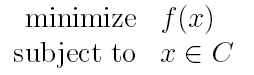
其中f是一个凸函数,C是一个凸集。根据先前介绍过的水平子集等概念,上面问题又可以等价写为:
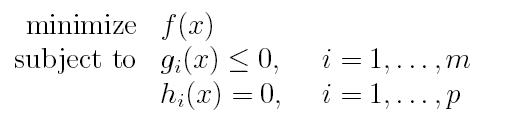
其中,g(x)是凸函数,h(x)是仿射函数。 也就是说,原约束集C被我们表示为一系列凸集的交集(数学上可以证明,凸集的交集还是凸集)。
1.4.4 局部最优(local optima)和全局最优(global optima)
局部最优:周围小范围 内没有比我小的点。
数学定义:
如果存在,对于所有的z:,有,那么就称x是一个局部最优点。
全局最优:我就是整个定义域中的最小的点。
数学定义:
如果对于定义域内的所有z,有,则称x是全局最优。
现在回到凸优化问题上, 对于凸优化问题,有一个很重要的结论:
对于凸函数来讲, 局部最优就是全局最优。证明如下:
我们用反证法证明。设是一个局部最优,但不是全局最优,于是我们假设全局最优是,那么我们有
由x的局部最优性质,我们有 :
存在,对于所有的z:,有
我们考虑和的凸组合:,无论在哪里,我们总可以找到一个,使得位于的邻域内,使得
另一方面,由凸函数性质,我们有:
由此得,这与矛盾, 于是我们证明了如果是局部最优,那么同时它也是全局最优。
1.5 常见凸优化问题
- 线性规划
如果和都是仿射函数,则凸优化问题变为了线性规划问题:

- 二次规划
线性规划中,如果变为一个凸二次函数,则凸优化问题变为二次规划:
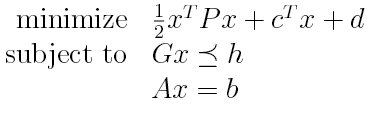
- 二次约束二次规划
和都是凸二次函数

- 半定规划
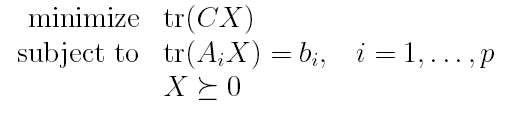
其中,是一个n维对称方阵,并且我们将它约束为半正定矩阵。都是对称矩阵。这和前面的问题有点不太相同,前面是优化一个向量,而这里是优化一个矩阵。
参考:
http://cs229.stanford.edu/section/cs229-cvxopt.pdf
本文转载自多个地方,仅用作个人学习,如需删除请见谅并联系本人。
1 梯度下降法
2 坐标下降法
1.首先给定一个初始点,如 X_0=(x1,x2,…,xn);
2.for x_i=1:n
固定除x_i以外的其他维度
以x_i为自变量,求取使得f取得最小值的x_i;
end
3. 循环执行步骤2,直到f的值不再变化或变化很小.
3 牛顿迭代法
牛顿迭代法(Newton’s method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
把f(x)在x0点附近展开成泰勒级数 f(x) = f(x0)+(x-x0)f’(x0)+(x-x0)^2*f”(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f’(x0)(x-x0)=0 设f’(x0)≠0则其解为x1=x0-f(x0)/f’(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f’(x(n))。
4 最小二乘法与梯度下降法区别
最小二乘是构建目标函数中的一种方法;
梯度下降是求解最优目标函数中的一种方法。
对于变量个数为2-3个的目标函数,可以直接用方程组的方式求解出来,这也就是我们常见的狭义上的最小二乘法。
对于变量个数多个的目标函数,这时,狭义的最小二乘法就难以胜任,而用梯度下降法求解就容易多了。
http://www.cnblogs.com/wacc/p/4870043.html
1.1 什么是凸集?
简单来说, 凸集是一个点集, 这个点集有一个性质, 就是在这个集合中任取不同的两个点x和y, 他们之间的线段(包括端点)上的点都属于这个点集,那么就说这个点集是一个凸集。
比如下图中左边的图形是凸集,而右边不是,因为我们可以找到两个点,使它们之间的线段上的点不在集合中

数学上,凸集的定义如下:
给定集合,,,如果有
我们就称集合C是凸集,我们把点称为x和y的凸组合。
1.2 什么是凸函数?
假设有一个函数,记其定义域为,如果是凸集,且在其中任取两个点,满足以下性质:
那么就称为凸函数。
注意:定义域是凸集这个要求不是必须的,其出发点只是为了使x,y的凸组合有定义
关于凸函数,直观上可以用下图来加深理解:

简单来说,我们在定义域任取两个点x,y, 连接他们得到一条线段,如果这个线段上的点都位于对应函数值上方,我们就说该函数是一个凸函数。
更进一步,如果且我们称是严格凸的。如果是凸函数,那么就是凹函数。如果是严格凸函数,那么就是严格凹函数。
1.3 凸函数的等价判别方法
上面我们讲了什么是凸函数,然而这个定义在现实中很难用于判断一个函数是不是凸的,因此介绍几个等价的定义。
1.3.1 一阶近似
假设函数是可导函数(也就是说的梯度在整个定义域上都存在),则是凸函数当且仅当 其定义域是凸集,且对于所有的有下式成立:
我们将叫做对f的一阶近似,其物理意义实际上是经过点x的切平面,我们用这个切平面上的点来近似。这个公式的含义是:如果f是凸函数,那么它的一阶近似值始终位于函数值的下方。

1.3.2 二阶近似
假设函数二阶可导(即海塞矩阵在定义域上都有定义),则f是凸函数当且仅当 其定义域是凸集且其海塞矩阵半正定,即:
可能有些同学忘了海塞矩阵长什么样了,这里提一下。假设我们的变量来自n维空间,即,我们记,即由n个变量组成的向量。那么海塞矩阵(记为H吧)是一个的方块矩阵,且
也就是说,是f(x)分别对和进行求导两次得到的。
1.4 凸优化问题
上面已经介绍了凸集和凸函数,是时候到凸优化了吧? 别急,在介绍凸优化概念之前再啰嗦两句。
1.4.1 水平子集(sublevel sets)
由凸函数的概念出发,我们可以引出水平子集(sublevel set)的概念。假定f(x)是一个凸函数, 给定一个实数,我们把集合
叫做水平子集。 也就是说水平子集是所有满足的点构成的集合。利用凸函数性质,我们可以证明水平子集也是凸集:
水平子集告诉我们,给凸函数添加一个上限,定义域内剩下的点构成的点集还是一个凸集。
1.4.2 仿射函数(affine functions)
数学上,我们把形如
的函数叫做仿射函数。其中,,一个向量。直观上理解,仿射函数将一个n维空间的向量通过线性变换A映射到m维空间,并在其基础上加上向量b,进行了平移。
同理,我们可以证明,点集
是一个凸集,证明略。
1.4.3 凸优化(convex optimization)
那么回到凸优化问题上来, 什么是一个凸优化问题?
一个凸优化问题可以定义为:
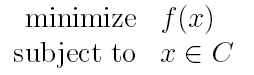
其中f是一个凸函数,C是一个凸集。根据先前介绍过的水平子集等概念,上面问题又可以等价写为:
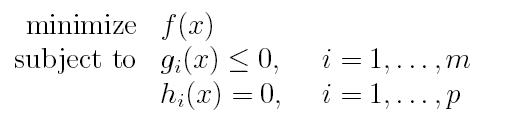
其中,g(x)是凸函数,h(x)是仿射函数。 也就是说,原约束集C被我们表示为一系列凸集的交集(数学上可以证明,凸集的交集还是凸集)。
1.4.4 局部最优(local optima)和全局最优(global optima)
局部最优:周围小范围 内没有比我小的点。
数学定义:
如果存在,对于所有的z:,有,那么就称x是一个局部最优点。
全局最优:我就是整个定义域中的最小的点。
数学定义:
如果对于定义域内的所有z,有,则称x是全局最优。
现在回到凸优化问题上, 对于凸优化问题,有一个很重要的结论:
对于凸函数来讲, 局部最优就是全局最优。证明如下:
我们用反证法证明。设是一个局部最优,但不是全局最优,于是我们假设全局最优是,那么我们有
由x的局部最优性质,我们有 :
存在,对于所有的z:,有
我们考虑和的凸组合:,无论在哪里,我们总可以找到一个,使得位于的邻域内,使得
另一方面,由凸函数性质,我们有:
由此得,这与矛盾, 于是我们证明了如果是局部最优,那么同时它也是全局最优。
1.5 常见凸优化问题
- 线性规划
如果和都是仿射函数,则凸优化问题变为了线性规划问题:

- 二次规划
线性规划中,如果变为一个凸二次函数,则凸优化问题变为二次规划:
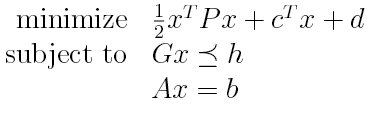
- 二次约束二次规划
和都是凸二次函数

- 半定规划
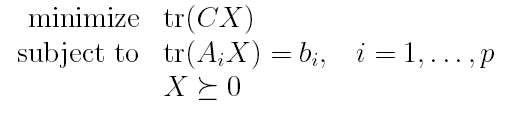
其中,是一个n维对称方阵,并且我们将它约束为半正定矩阵。都是对称矩阵。这和前面的问题有点不太相同,前面是优化一个向量,而这里是优化一个矩阵。
参考:
http://cs229.stanford.edu/section/cs229-cvxopt.pdf
