Description
给你N个点的无向图 (1 <= N <= 15,000),记为:1…N。
图中有M条边 (1 <= M <= 30,000) ,第j条边的长度为: d_j ( 1 < = d_j < = 1,000,000,000).
现在有 K个询问 (1 < = K < = 20,000)。
每个询问的格式是:A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
Input
第一行: N, M, K。
第2..M+1行: 三个正整数:X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。
第M+2..M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
Output
对每个询问,输出最长的边最小值是多少。
Sample Input
6 6 8
1 2 5
2 3 4
3 4 3
1 4 8
2 5 7
4 6 2
1 2
1 3
1 4
2 3
2 4
5 1
6 2
6 1
Sample Output
5
5
5
4
4
7
4
5
HINT
1 <= N <= 15,000
1 <= M <= 30,000
1 <= d_j <= 1,000,000,000
1 <= K <= 15,000
分析:
其实这道题的题意简化一下就是
在一个图中询问任意两点之间的路径
使得路径上的最大边最小
感觉这个题目似曾相识
没错就是货车运输
只要先建立一棵最小生成树
在树上跑lca就可以了
但是今天我们不要用这么low的算法
(没事找事)
我们就引进一种新的数据结构
kruskal重构树:
什么是kruskal重构树呢:
kruskal重构树是个挺好玩的东西
可以拿来处理一些最小生成树的边权最值问题
这里我们Kruskal连边时并不直接连边
而是新建一个节点x
将两个点所在子树都连到x的儿子上
这样生成的树有一些十分优美的性质:
1.二叉树(好吧意义不大)
2.原树与新树两点间路径上边权(点权)的最大值相等
3.子节点的边权小于等于父亲节点(大根堆)
4.原树中两点之间路径上边权的最大值等于新树上两点的LCA的点权
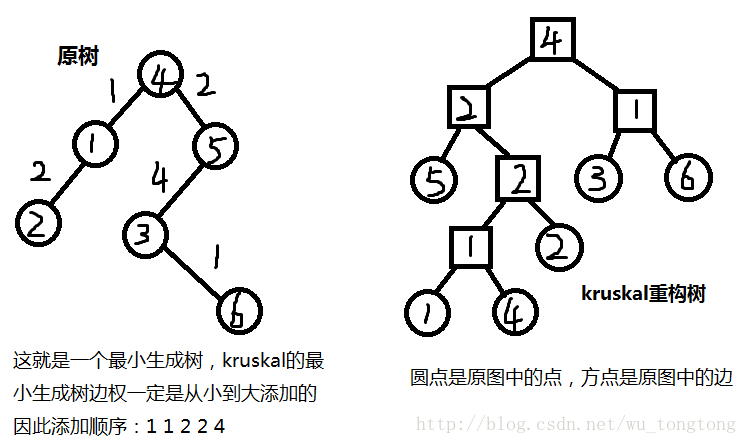
看图理解一下吧
看一下性质的体现:
1.不用说了
2.原树上2—>5:2,新树上也是
3.不用说了
4.1—>6:4
确认满足性质
那如果我们建出了kruskal重构树,处理询问只要找一下lca就可以了
那怎么构建kruskal重构树呢:
其实就像构建最小生成树一样
只不过并不直接连边
而是新建一个节点x
将两个点所在子树都连到x的儿子上
有点像并查集哈
tip
1A
这是我自己yy的写法,异常丑陋
这里写代码片
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=30005;
int n,m,k;
struct node{
int x,y,nxt;
};
node way[N<<2];
struct nd{
int x,y,v;
};
nd e[N];
int deep[N<<1],fa[N<<1],f[N<<1][20],lg,st[N<<1],tot=0,tt=0,z[N<<1];
int cmp(const nd &a,const nd &b)
{
return a.v<b.v;
}
int find(int a) //路径压缩
{
if (fa[a]!=a) fa[a]=find(fa[a]);
return fa[a];
}
void add(int u,int w)
{
tot++;
way[tot].x=u;way[tot].y=w;way[tot].nxt=st[u];st[u]=tot;
tot++;
way[tot].x=w;way[tot].y=u;way[tot].nxt=st[w];st[w]=tot;
}
void kruskal()
{
int i,j,o=0;
tt=n;
for (i=1;i<=n;i++) fa[i]=i;
for (i=1;i<=m;i++)
{
int f1=find(e[i].x);
int f2=find(e[i].y);
if (f1!=f2)
{
tt++;
add(f1,tt); //连到新点上
add(f2,tt);
fa[tt]=tt;fa[f1]=tt;fa[f2]=tt;
z[tt]=e[i].v; //记录点权
o++;
}
if (o==n-1) break;
}
lg=log(tt)/log(2);
}
void dfs(int x,int pa,int dep)
{
deep[x]=dep;
f[x][0]=pa;
for (int i=st[x];i;i=way[i].nxt)
if (way[i].y!=pa)
dfs(way[i].y,x,dep+1);
}
void cl()
{
int i,j;
for (i=1;i<=lg;i++)
for (j=1;j<=tt;j++)
f[j][i]=f[f[j][i-1]][i-1];
}
int lca(int u,int w)
{
if (deep[u]<deep[w]) swap(u,w);
int d=deep[u]-deep[w];
if (d)
for (int i=0;i<=lg&&d;i++,d>>=1)
if (d&1)
u=f[u][i];
if (u==w) return z[u];
for (int i=lg;i>=0;i--)
if (f[u][i]!=f[w][i])
{
u=f[u][i];w=f[w][i];
}
return z[f[u][0]];
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
for (int i=1;i<=m;i++)
scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].v);
sort(e+1,e+1+m,cmp);
kruskal();
dfs(tt,0,1);
cl();
for (int i=1;i<=k;i++)
{
int u,w;
scanf("%d%d",&u,&w);
printf("%d\n",lca(u,w));
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
Description
给你N个点的无向图 (1 <= N <= 15,000),记为:1…N。
图中有M条边 (1 <= M <= 30,000) ,第j条边的长度为: d_j ( 1 < = d_j < = 1,000,000,000).
现在有 K个询问 (1 < = K < = 20,000)。
每个询问的格式是:A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
Input
第一行: N, M, K。
第2..M+1行: 三个正整数:X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。
第M+2..M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
Output
对每个询问,输出最长的边最小值是多少。
Sample Input
6 6 8
1 2 5
2 3 4
3 4 3
1 4 8
2 5 7
4 6 2
1 2
1 3
1 4
2 3
2 4
5 1
6 2
6 1
Sample Output
5
5
5
4
4
7
4
5
HINT
1 <= N <= 15,000
1 <= M <= 30,000
1 <= d_j <= 1,000,000,000
1 <= K <= 15,000
分析:
其实这道题的题意简化一下就是
在一个图中询问任意两点之间的路径
使得路径上的最大边最小
感觉这个题目似曾相识
没错就是货车运输
只要先建立一棵最小生成树
在树上跑lca就可以了
但是今天我们不要用这么low的算法
(没事找事)
我们就引进一种新的数据结构
kruskal重构树:
什么是kruskal重构树呢:
kruskal重构树是个挺好玩的东西
可以拿来处理一些最小生成树的边权最值问题
这里我们Kruskal连边时并不直接连边
而是新建一个节点x
将两个点所在子树都连到x的儿子上
这样生成的树有一些十分优美的性质:
1.二叉树(好吧意义不大)
2.原树与新树两点间路径上边权(点权)的最大值相等
3.子节点的边权小于等于父亲节点(大根堆)
4.原树中两点之间路径上边权的最大值等于新树上两点的LCA的点权
看图理解一下吧
看一下性质的体现:
1.不用说了
2.原树上2—>5:2,新树上也是
3.不用说了
4.1—>6:4
确认满足性质
那如果我们建出了kruskal重构树,处理询问只要找一下lca就可以了
那怎么构建kruskal重构树呢:
其实就像构建最小生成树一样
只不过并不直接连边
而是新建一个节点x
将两个点所在子树都连到x的儿子上
有点像并查集哈
tip
1A
这是我自己yy的写法,异常丑陋
这里写代码片
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=30005;
int n,m,k;
struct node{
int x,y,nxt;
};
node way[N<<2];
struct nd{
int x,y,v;
};
nd e[N];
int deep[N<<1],fa[N<<1],f[N<<1][20],lg,st[N<<1],tot=0,tt=0,z[N<<1];
int cmp(const nd &a,const nd &b)
{
return a.v<b.v;
}
int find(int a) //路径压缩
{
if (fa[a]!=a) fa[a]=find(fa[a]);
return fa[a];
}
void add(int u,int w)
{
tot++;
way[tot].x=u;way[tot].y=w;way[tot].nxt=st[u];st[u]=tot;
tot++;
way[tot].x=w;way[tot].y=u;way[tot].nxt=st[w];st[w]=tot;
}
void kruskal()
{
int i,j,o=0;
tt=n;
for (i=1;i<=n;i++) fa[i]=i;
for (i=1;i<=m;i++)
{
int f1=find(e[i].x);
int f2=find(e[i].y);
if (f1!=f2)
{
tt++;
add(f1,tt); //连到新点上
add(f2,tt);
fa[tt]=tt;fa[f1]=tt;fa[f2]=tt;
z[tt]=e[i].v; //记录点权
o++;
}
if (o==n-1) break;
}
lg=log(tt)/log(2);
}
void dfs(int x,int pa,int dep)
{
deep[x]=dep;
f[x][0]=pa;
for (int i=st[x];i;i=way[i].nxt)
if (way[i].y!=pa)
dfs(way[i].y,x,dep+1);
}
void cl()
{
int i,j;
for (i=1;i<=lg;i++)
for (j=1;j<=tt;j++)
f[j][i]=f[f[j][i-1]][i-1];
}
int lca(int u,int w)
{
if (deep[u]<deep[w]) swap(u,w);
int d=deep[u]-deep[w];
if (d)
for (int i=0;i<=lg&&d;i++,d>>=1)
if (d&1)
u=f[u][i];
if (u==w) return z[u];
for (int i=lg;i>=0;i--)
if (f[u][i]!=f[w][i])
{
u=f[u][i];w=f[w][i];
}
return z[f[u][0]];
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
for (int i=1;i<=m;i++)
scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].v);
sort(e+1,e+1+m,cmp);
kruskal();
dfs(tt,0,1);
cl();
for (int i=1;i<=k;i++)
{
int u,w;
scanf("%d%d",&u,&w);
printf("%d\n",lca(u,w));
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114