最小生成树
源于华文慕课网
PRIM 算法
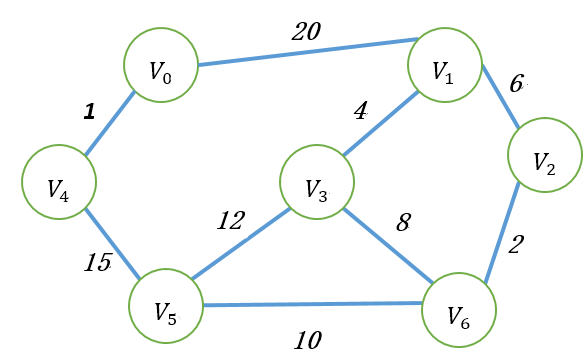
- 从图中任意一点开始(例如V0),首先把这个顶点包括在MST,U=(V*,E*)里。【初始V*={0},E*={}
- 在一端已在MST里,另一端还不在MST里的边中,找一条权值最小的边VpVq,并将此Vq包括进MST里
- 如此进行下去,每次往MST里加一个顶点和一条权值最小的边,直到把所有顶点都加入MST里
代码
void Prim(Graph& G, int s, Edge* &MST) // s是起始点,MST存边
{
int MSTtag = 0; // 最小生成树的边计数
MST = new Edge[G.VerticesNum()-1]; // 为数组MST申请空间
Dist *D;
D = new Dist[G.VerticesNum()]; // 为数组D申请空间
for (int i=0;i<g.verticesNum();i++){ // 初始化Mark和D数组
G.Mark[i] = UNVISITED;
D[i].index = i;
D[i].length = INF;
D[I].pre = s;
}
D[s].length = 0; // 开始顶点标记为VISITED
G.Mark[s] = VISITED;
int v = s;
for (int i=0;i<G.VerticesNum()-1;i++){
// 因为v的加入,需要刷新与v相邻接的顶点的D值
for (Edge e = G.FirstEdge(v); G.IsEdge(e); e = G.NextEdge(e)){
if (G.Mark[G.ToVertex(e)]!=VISITED && D[G.ToVertex(e)].length>e.weight){
D[G.ToVertex(e)].length = e.weight;
D[G.ToVertex(e)].pre = v;
}
}
v = minVertex(G,D) // 在D数组中找最小值记为v
if (v == -1) retrun; // 非连通,有不可达顶点
G.Mark[v] = VISITED; //标记访问过
Edge edge(D[v].pre, D[v].index, D[v].length); // 保存边
AddEdgetoMST(edge,MST,MSTtag++); // 将边加入MST
}
}
// 在Dist数组中找最小值
int minVertex(Graph& G,Dist* &D)
{
int i,v = -1;
int MinDist = INF;
for (i=0; i<G.VerticesNum();i++){
if((G.Mark[i] == UNVISITED) && (D[i] < MinDist)){
v = i; //保存当前发现的最小距离顶点
MinDist = D[i];
}
}
return v;
}Prim算法的时间复杂度
- Prim算法非常类似于Dijkstra算法
- Prim算法框架与Dijkstrra算法相同
- Prim算法中的距离值不需要累积,直接用最小边
- 本算法通过直接比较D数组元素,确定代价最小的边就需要总时间O(n2);取出权最小的顶点后,修改D数组共需要时间O(e),因此共需要花费O(n2)的时间
- 算法适用于稠密图
- 对于稀疏图,可以像Dijkstra算法那样用堆来保持距离值
Kruskal 算法
- 首先将G中的n个顶点看成独立的n个连通分量,这时的状态是有n个顶点而无边的森林,可以记为<V,{}>
- 然后在E中选择代价最小的边,若该边依附于两个不同的分支,那么将这条边加入到T中,否则舍去这条边而选择下一条代价最小的边
- 依此类推,直到T中所有顶点都在同一个连通分量中为止,此时得到图G的最小生成树
代码
void Kruskal(Graph& G, Edge* &MST) // MST存最小生成树的边
{
ParTree<int> A(G.VerticesNum()); // 等价类
MinHeap<Edge> H(G.EdgesNum()); // 最小堆
MST = new Edge[G.VerticesNum()-1]; // 为数组MST申请空间
int MSTtag = 0; // 最小生成树的边计数
for (int i=0; i<G.VerticesNum(); i++){ // 将所有边插入最小堆H中
for (Edge e=G.FirstEdge(i); g.IsEdge(e); e=g.NextEdge(e)){
if(G.FromVertex(e) < G.ToVertex(e)) // 防重复边
H.Insert(e);
}
}
int EquNum = g.VerticesNum(); // 开始有n个独立顶点等价类
while (EquNum > 1){ // 当等价类的个数大于1时合并等价类
if (H.isEmpty()){
cout<<"不存在最小生成树。"<<endl;
delete [] MST;
MST = NULL; //释放空间
return;
}
Edge e = H.RemoveMin(); // 取权值最小的边
int from = G.FromVertex(e); // 记录该条边的信息
int to = G.ToVertex(e);
if (A.Different(from,to)){ // 若边e的两个顶点不在一个等价类
A.Union(from,to); // 合并边的两个顶点所在的等价类
AddEdgetoMST(e,MST,MSTtag++); // 将边e加到MST
EquNum--; // 等价类的个数减1
}
}
}Kruskal算法的代价
- 使用了路径压缩,Different()和Union()函数几乎是常数
- 假设可能对几乎所有边都判断过了
- 则最坏情况下算法时间代价为Θ(elog e),即堆排序的时间
- 通常情况下只找了略多于n次,MST就已经生成
- 时间代价接近于 Θ(nlog e)