主要内容:算法复杂度
在上一篇文章中说到,一个算法是解决某一类问题的步骤的描述,现在来通过几个例子理解一下算法。
选择排序 :实现把n个整数从小到大排序。
思想:在余下未排好序的整数中寻找最小的整数,插入到前面已经排好序的数字后面。
代码实现:
public int[] selectSort(int[] array){
//得到数组的长度
int len = array.length;
//定义最小数字
for(int i=0;i<len-1;i++){
//定义当前最小的数
int minNum = array[i];
for(int j=i;j<len;j++){
if(array[j]<minNum){
int temp = array[j];
array[j] = minNum;
minNum = temp;
}
}
int temp = array[i];
array[i] = minNum;
minNum = temp;
}
return array;
}
选择排序 = 找出最小数+交换至合适位置
时间复杂度与空间复杂度:
什么是好的算法? 衡量算法好坏的指标有哪些呢? 主要衡量算法好坏的指标主要有两个
空间复杂度 S(n) ——根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限,造成程序非正常中断。
上一篇文章中 例2 PrintN(int n) 递归实现 S(n) 太大。
S(n) = c · n 其中:n是需要打印的整数的个数,是变量; c是1个单位的内存空间占用存储单元的长度,为固定常数。
时间复杂度 T(n) ——根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。
上一篇文章中 例 3 的秦九韶算法的T(n)比较小
T1(n) = c · n 其中:n是多项式的阶数,是变量; c是执行1次加法和乘法需要的时间,为固定常数。
而简单直接算法的T(n)比较大: T2(n) = c1n2+c2n , 其中:n是多项式的阶数,是变量; c1是执行1/2次乘法需要的时间; c2是执行1次加法和1/2次乘法需要的时间,都是固定常数。
我们经常关注下面两种复杂度:
最坏情况复杂度: Tworst(n)
平均复杂度: Tavg(n)
显然: Tavg(n) ≤ Tworst(n)。 对 Tworst(n) 的分析往往比对 Tavg(n)的分析容易。
所以我们一般分析的都是最坏情况复杂度。
如何来“度量”一个算法的时间复杂度呢?
首先,它应该与运行该算法的机器和编译器无关;
其次,它应该与要解决的问题的规模 n 有关; (有时,描述一个问题的规模需要多个参数)
再次,它应该与算法的“1步”执行需要的工作量无关!
所以,在描述算法的时间性能时,人们只考虑宏观渐近性质,即当输入问题规模 n“充分大”时,观察算法复杂度随着 n 的“增长趋势”: 当变量n不断增加时,解决问题所需要的时间的增长关系。
比如:线性增长 T(n) = c·n 即问题规模n增长到2倍、3倍……时,解决问题所需要的时间T(n)也是增长到2倍、3倍……( 与c无关 )
平方增长: T(n) = c·n2 即问题规模n增长到2倍、3倍……时,解决问题所需要的时间T(n)增长到4倍、9倍…… ( 与c无关 )
引入下面几种数学符号:
[定义1.1] T (n) = O(f(n)) 表示存在常数c > 0, n0 > 0 ,
使得当 n ≥ n0 时有 T (n) ≤ c f(n)
f(n) 是 T(n)的某种上界;
前文 例3 中秦九韶算法的时间复杂度是O(n) ,而简单直接法的时间复杂度是O(n2) 。
[定义1.2] T (n) = Ω(g(n)) 表示存在常数c > 0, n0 > 0 ,
使得当 n ≥ n0 时有 T (n) ≥ c g(n)
f(n) 是 T(n)的某种下界;
[定义1.3] T (n) = Θ(h(n)) 表示
T (n) = O(h(n)) 同时T (n) = Ω(h(n))
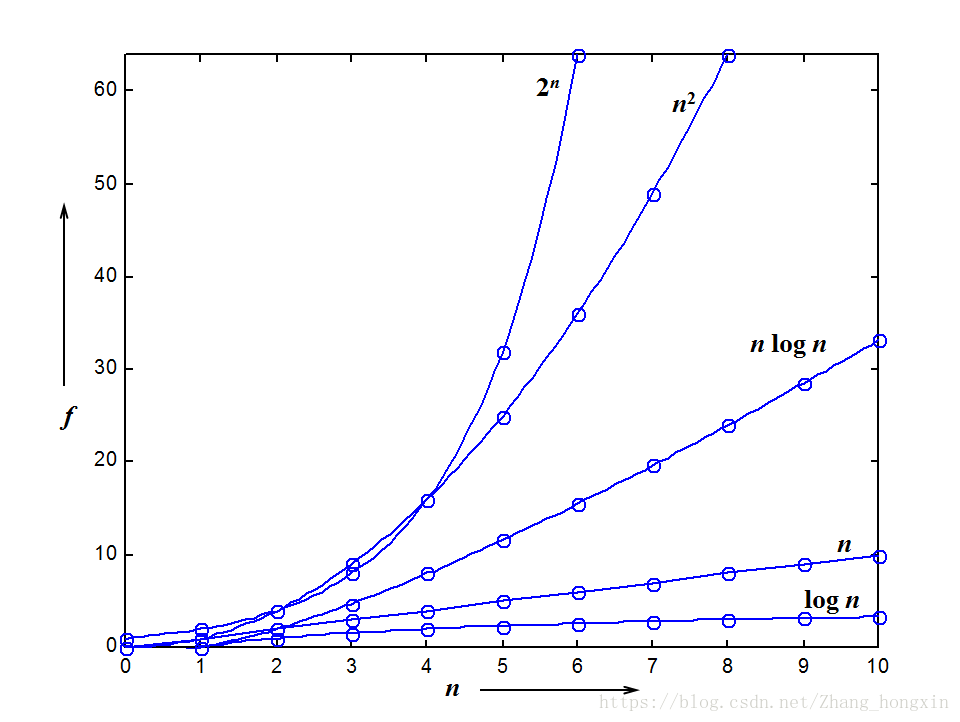
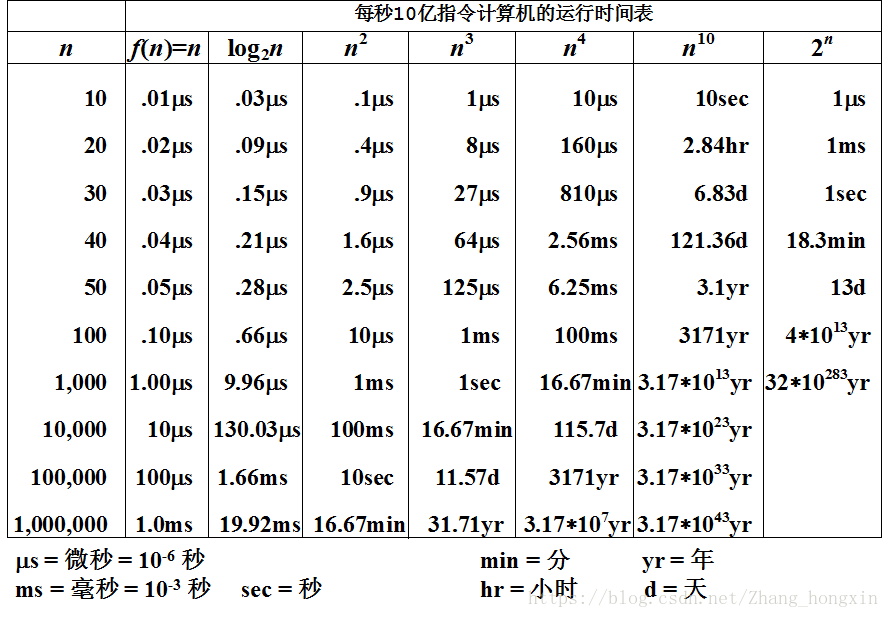
常用函数增长表
对给定的算法做复杂度分析时:
(1) 若干层嵌套循环的时间复杂度等于各层循环次数的乘积再乘以循环体代码的复杂度。
例如下列2层嵌套循环的复杂度是O(N2):
for ( i=0; i<N; i++ )
for ( j=0; j<N; j++ )
{ x = y*x + z; k++; }
(2) if-else 结构的复杂度取决于if的条件判断复杂度和两个分枝部分的复杂度,总体复杂度取三者中最大。即对结构:
if (P1) /* P1的复杂度为 O(f1) */
P2; /* P2的复杂度为 O(f2) */
else
P3; /* P3的复杂度为 O(f3) */
总复杂度为 max( O(f1), O(f2), O(f3) ) 。
用不同复杂度的算法解决问题:
给定 n个整数(可以是负数)的序列{a1, a2, …, an} , 求函数 f(i, j) = max( 0, 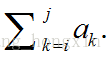
方法一:
/**
* 给定 n个整数(可以是负数)的序列{a1, a2, …, an} ,
*/
public int maxSubSequence(int [] arr,int n){
int maxNum =0;
for(int i =0;i<n;i++){ //定义序列的最左端
for(int j = i;j<n;j++){ //定义序列最右端
int thisNum = 0; //当前子序列长度
for(int k=i;k<j;k++){ //当前子序列
thisNum+=arr[k];
if(thisNum>maxNum){
maxNum=thisNum;
}
}
}
}
return maxNum;
}此方法需要三层for循环,时间复杂度为O(n3)。
方法二:
public int maxSubSequence2(int [] arr,int n){
int maxNum =0;
for(int i =0;i<n;i++){ //定义序列的最左端
int thisNum = 0;
for(int j = i;j<n;j++){ //定义序列最右端
thisNum+=arr[j]; //只需要不断累加当前子序列即可,不用循环
if(thisNum>maxNum){
maxNum=thisNum;
}
}
}
return maxNum;
}此方法 的算法复杂度为O(n2)
方法三:
public static int MaxSubSum(int a[],int Left,int Right){
int MaxLeftSum,MaxRightSum;
int MaxLeftBorderSum,MaxRightBorderSum;
int Center;
if(Left==Right)
if(a[Left]>0)
return a[Left];
else
return 0;
Center=(Left+Right)/2;
MaxLeftSum =MaxSubSum(a,Left,Center); //第一句
MaxRightSum=MaxSubSum(a,Center+1,Right);//第二句
MaxLeftBorderSum=0;
int LeftBorderSum=0;
for(int i=Center;i>=Left;i--) {
LeftBorderSum+=a[i];
if(LeftBorderSum>MaxLeftBorderSum)
MaxLeftBorderSum=LeftBorderSum;
}
MaxRightBorderSum=0;
int RightBorderSum=0;
for(int i=Center+1;i<=Right;i++){
RightBorderSum+=a[i];
if(RightBorderSum>MaxRightBorderSum)
MaxRightBorderSum=RightBorderSum;
}
return Max3(MaxLeftSum,MaxRightSum,MaxLeftBorderSum+MaxRightBorderSum);
}
private static int Max3(int a, int b, int c) {
int max = 0;
if(a>b){
if(a>c){
max = a;
}else{
max=c;
}
}else{
if(b>c){
max=b;
}else{
max=c;
}
}
return max;
}此方法的时间复杂度为O(nlogn)
方法四:
public static int maxSubSequence4(int [] arr,int n){
int maxNum =0;
int thisNum = 0;
for(int i =0;i<n;i++){ //定义序列的最左端
thisNum+=arr[i];
if(thisNum>maxNum){
maxNum = thisNum;
}
if(thisNum<0){
thisNum=0;
}
}
return maxNum;
}
此方法时间复杂度为O(n)。
由此可见不同的算法,对解决同一问题的效率相差太多了。
未完待续。
参考资料:浙江大学-数据结构课程-陈越